应用统计类专业探究性教学模式探索与实践
——以变量选择准则为例
(温州大学 数学与信息科学学院,浙江 温州 325035)
应用统计类专业探究性教学模式探索与实践
——以变量选择准则为例
徐安察,王玮明
(温州大学 数学与信息科学学院,浙江 温州 325035)
变量选择准则是《回归分析》中很重要的章节,并且是学习回归分析的难点.采用探究式教学讲授变量选择准则,效果十分显著.其教学过程包括:提出问题、进行探究活动、教师引导得出结论、教师提出新的研究问题、学生课后探索.在进行探究教学活动时,教师要从研究计划、教学目标等几方面做好工作.
变量选择准则;回归分析;探究式教学;R语言
1 引言
随着高等教育国际化不断发展,我国已成为高等教育大国,正在建设高等教育强国,经济社会发展与高等教育的关系更加密切.科技自主创新能力和创新型人才正成为决定国家和区域竞争力的关键因素.如何培养创新型人才是各大高校所面临的难题,这需要高校教师在教学中不断探索.探究式教学作为一种新的教学手段正逐步在日常教学中使用[1].
《现代统计分析方法》是温州大学应用统计专业的主干课程,主要内容包括《多元统计分析》和《回归分析》组成.回归分析是处理多变量之间关系的一种统计方法和技术,应用非常广泛[2].通常来讲,回归分析是通过确定因变量和自变量之间的数量关系,建立回归方程(或称回归模型),并根据统计数据估计模型中的所有参数,然后评价模型是否能够很好地拟合观测数据,如果拟合程度高,就可以根据回归模型预测因变量的发展态势.回归分析按照自变量的个数,可分为一元和多元回归分析.一元回归分析的内容比较简单,学生能够很好地掌握,但是多元回归分析由于涉及到多变量,无论是模型解释还是参数估计,对学生而言都比较抽象,很难理解,特别是当个别参数检验不显著时,如何对模型进行改进,或者选择一个更优的模型来描述因变量与自变量之间的关系是多元回归分析的重难点,也是学生在处理实际数据问题必须掌握的一个方法.为了引导学生积极主动地学习回归分析,在教学过程中,基于统计软件R语言,我们使用了探究性教学方法,并充分利用了多媒体技术.
2 变量选择准则探究式教学过程
变量选择准则是在全子集回归章节中提到,基于准则可以选择“最优模型”.在前面的授课当中已经提到:模型中变量个数增多,拟合效果会变好,但是预测效果会变差.教学中使用R语言自带数据集(swiss),该数据收集了瑞士每个县的生产力y及五个自变量(从事农业生产的男性比例、入伍者考试得高分比例、入伍者受过初等教育以上的比例、信天主教比例以及一岁以下婴儿死亡率),具体数据见文献[3].数据分析的目标是找出影响生产力的因素.
2.1 提出研究问题,分析因果,由学生思考、探究
根据数据,利用R语言中做回归分析的函数lm()来分析数据,得到每个回归系数的估计值以及显著性检验P值,让学生观察哪些参数不显著,在发现对因变量不显著之后,启发学生根据上节课学习的全子集回归来分析这个问题.利用软件画出每个回归模型的误差平方和SSE,如图1所示:

图1 不同模型的误差平方和
图1中的标号表示对应模型的误差平方和,比如第一个“3”,表示y对做回归之后模型误差平方和的值.教师让学生观察是不是参数最多的模型,其对应的误差平方和最小.在得到肯定的回答之后,引出本节课的问题:用什么标准去评价模型的好坏?
2.2 在问题的引申中设计方案,开展探究性教学活动
教师继续提出问题:误差方差的无偏估计是什么?用无偏估计是否可以作为评价模型好坏的标准呢?学生结合之前学过的内容,可以知道的无偏估计为,然后教师画出不同模型的无偏估计值,如图2所示:
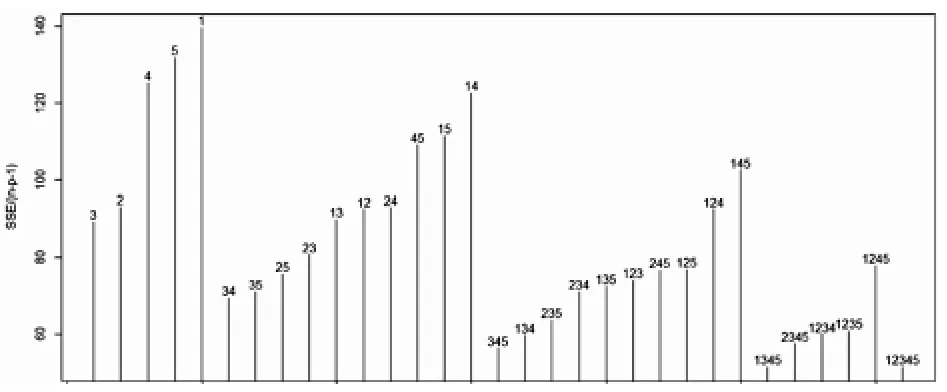
图2 不同模型的
让学生去发现该图与残差平方和图之间的差别,进而说明跟模型中变量个数无关,可以作为选择模型好坏的标准,然后引出变量选择的第一个准则:调整的复判定系数=1-,其中SST是因变量观测值的利差平方和,是一个常数,因此由决定,并且其值越大说明模型越好.画出图3让学生有直观认识:
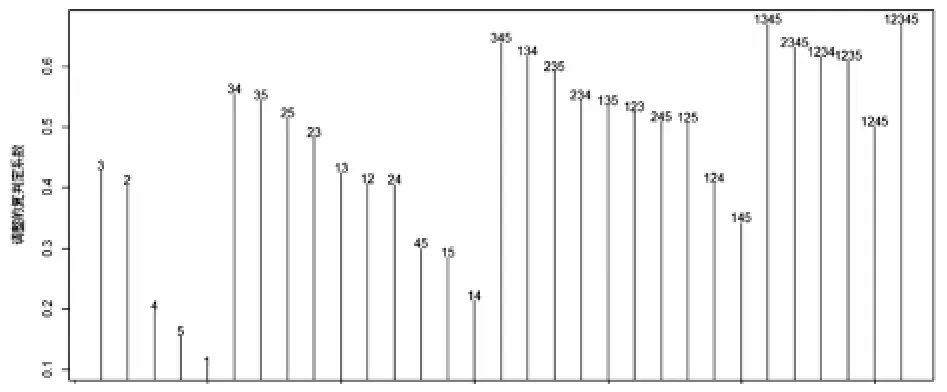
图3 不同模型的
在讲解新的准则之前,首先给学生讲述Akaike发现AIC准则的故事,并引出AIC准则为:AIC=.教师给学生解释AIC准则的含义:SSE代表模型拟合的好坏,p代表模型的复杂程度,因此AIC准则在模型拟合优度和复杂程度找到一个最佳的平衡点,其值越小越好.针对上述例子,画出各个模型的AIC,如图4所示:

图4 不同模型的
针对这两个准则,教师给出总结如何设计一个变量选择准则:(1)模型拟合优度,在和AIC中都是用SSE来刻画;(2)模型复杂程度或惩罚项,在中用来作为模型拟合优度的惩罚,而在AIC中用2p作为惩罚.
2.3 教师引导学生深入研究,培养学生的实践能力和创新能力
教师基于本节课的内容给出研究任务:在诊断异常值时使用删除残差来检验,第i个观测值的删除残差为,其中为第i个观测值的残差,是帽子矩阵的第i个主对角线元素,且,是否可以用删除残差平方和作为准则来选择变量?因为删除残差平方和包含了模型拟合优度()和模型复杂程度(因为).
对于课堂中使用的数据,教师画出各个模型的删除残差平方和图,如图5所示.学生观察后发现用删除残差平方和选择的最优模型与上述两个准则是一样的.教师让学生研究是不是对所有的数据都有类似的结果?
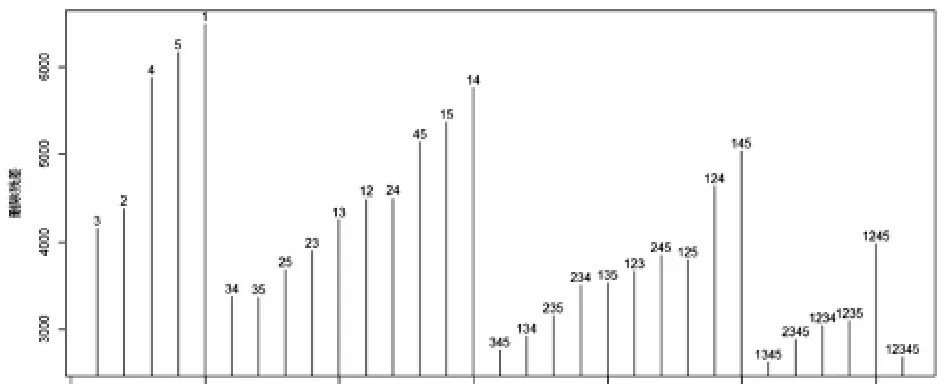
图5 不同模型的删除残差平方和
3 思考与讨论
探究式教学要求教师要具有一定的创新精神和创新意识,并有大量的研究基础,其次要给学生营造一个探究性的教学环境,给学生探索的时间和空间.在采用探究式教学模式进行教学活动时,教师要做好以下几方面的工作[4-6]:
(1)精心设计教学计划,明确教学目标.探究式教学是为了培养学生的综合素质,其关键是要制订一份全面详细的教学计划,确定明确的教学目标.教师要选择适合探究式教学法的教学内容,对学生的兴趣、知识水平、现有的探究能力等进行适当的评估,以便能够扩展学生的基本技能、培养学生的创新精神.
(2)正确定位自身在教学中的地位和作用.教师要认识到自己不仅仅是知识的传授者,更是组织者、参与者、研究者,甚至成为学习者.
(3)精心组织教学,为学生提供平台去发现和研究.要努力引导学生认真观察和研究提出的问题,然后发现一些新的问题去探索.
在“变量选择准则”探究式教学过程中,教师针对变量选择准则引导学生从多个角度进行渐进深化的再认识,从不同角度介绍变量选择准则,并结合之前学过的内容,构造新的准则,使学生懂得可以在已有知识的基础进行方法创新,培养了学生的创新能力.课堂上,教师坚持“以学生为中心”的原则,创造空间让学生去发现问题,发挥学生的学习积极性,引导学生去探究,激励学生创新.与传统的教学模式相比,探究式教学不仅能让学生更好地理解所学的知识,而且更有利于培养学生的学习能力和创新能力,是创新教育的一种有效途径,也必将使统计类专业学生数学素质教育和创新教育得到更好更快地发展.
〔1〕赵祥麟.杜威教育论著选[M].上海:华东师范大学出版社,1981.
〔2〕何晓群,刘文卿.应用回归分析[M].北京:中国人民大学出版社,2007.
〔3〕R语言.http://www.r-project.org/.
〔4〕马忠林.数学教学论[M].南宁:广西教育出版社,1996.
〔5〕霍益萍.研究性学习[M].南宁:广西教育出版社,2001.
〔6〕应俊峰.研究性学习的实施与管理[M].南昌:江西教育出版社,2002.
G642.0
A
1673-260X(2014)10-0007-02
温州大学精品资源共享课《数学模型与实验》、系列教改项目《数学与应用数学专业探究性教学模式研究与实践》及应用数学优秀教学团队建设资助项目

