遗传算法优化BP神经网络的非线性函数拟合研究

王光明，王爱平

（安徽大学 计算机科学与技术学院，安徽 合肥 230601）

遗传算法优化BP神经网络的非线性函数拟合研究

王光明，王爱平

（安徽大学 计算机科学与技术学院，安徽 合肥 230601）

传统的BP神经网络收敛速度慢，以及该算法的不完备性，易陷于局部极小，全局最优无法保证能收敛到等缺点.针对BP神经网络的缺陷，该文提出了遗传算法，利用遗传算法优化BP神经网络权值和阈值，使得训练了BP神经网络预测模型得到了最优解.采用遗传算法优化BP神经网络的算法，并以此结合算法来研究非线性函数拟合的问题.从实验结果表明，基于遗传算法优化的BP神经网络的非线性函数拟合具有较强的收敛性和鲁棒性，并且有了更高的预测精度.

神经网络；BP神经网络；遗传算法；非线性函数

BP（BackPropagation，BP）神经网络，是1986年由Rumelhart和McCelland为首的科学家小组提出.BP神经网络是一种按着误差逆传播算法训练的多层前馈网络，它也是目前应用比较广泛的算法.BP神经网络，是能学习和存贮大量的输入—输出模式映射关系，因此在工程中有着很广泛的应用.工程系统状态方程复杂，难以用数学方法来建模来处理，在此情况下，可以建立BP神经神经网络表达这些非线性系统.该方法把未知系统看成是一个黑箱，首先用系统输入输出数据训练BP神经网络，使网络能够表达该未知函数，然后就可以用训练好的BP神经网络预测系统输出.BP神经网络具有较高的拟合能力，但是网络预测结果有一定的误差，某些样本点的预测误差较大.在经过增加多隐含层BP神经网络得到了一些改善，但是也增加了运行时间.BP神经网络还受到节点数的影响，如果节点数过少，BP神经网络就不能建立复杂的映射关系，这样网络误差较大，反之，过多的情况，就会增加学习时间，并且有可能出现“过拟合”的情况（就是训练样本预测准确，但是其他样本预测误差较大）.避免上面的问题，提出了一种方法，采用遗传算法，从而可以建立遗传算法优化的BP神经网络的非线性函数拟合.

遗传算法（GeneticAlgorithm，GA），是一种全局优化搜索的迭代算法，把GA与BP神经网络相互融合在一起，用GA的优点来优化BP神经网络的权值和阈值，这样使得BP神经网络的泛化能力更强，并且收敛性也很大程度上的提高，在一定程度上也使得BP神经网络的学习能力得到了提高.基于上述原由，本文从非线性函数拟合的角度出发，提出了遗传算法优化BP神经网络的算法，降低了陷于局部最小的情况并能够使得BP有更佳的收敛精度.

遗传算法优化BP神经网络的算法的流程：BP神经网络的结构的确定，接着遗传算法的优化和BP神经网络预测的三个部分构成.

1 BP神经网络和遗传算法

图1-1 BP神经网络拓扑结构图

1.1 BP神经网络

神经网络是一种模仿人脑结构及其功能的智能处理系统[1].该方法通过对样本的学习训练，不断改变网络的连接权值以及拓扑结构，以使网络的输出不断的接近期望的输出.BP神经网络是神经网络的一种，它也是目前得到较为广泛的应用，并且也是比较成熟的人工神经网络算法.BP神经网络主要特点是信号前向传递，误差反向传播.在前向传递中，输入信号从输入层经隐含层处理，直至到输出层输出信号.每一层的神经元状态只会影响下一层的神经元状态.在输出层得不到期望的输出结果，则会转向反向传播，根据所预测误差调整网络权值和阈值，从而得到不断逼近期望输出结果.BP神经网络的拓扑结构如图1-1所示.

图1-1，其中的X1,X2,…,Xn是BP神经网络输入层提供的输入数据，Wij，Wjk则是BP神经网络的权值，BP神经网络的预测值则是输出层输出的数据Y1,Y2,…,Yn.训练网络是BP神经网络预测前需要提前做的，因为训练可以使得网络具有联想记忆和预测能力.其中BP神经网络的训练有以下几个过程[2]：

第一步：网络初始化.基于系统输入输出序列(X,Y)，来确定网络输入层节点数n，输出层节点数m，以及隐含层节点数l.初始化连接权值wij，wjk，之后需要隐含层的阈值a和输出层的阈值b初始化，并且给出函数；

第二步：隐含层输出计算.

依据输入的X向量，经过输入层和隐含层之间的权值wij处理得到，其中的f为激励函数；

第三步：输出层输出计算.第二步得到的H，连接权值wjk与阈值b，就可以计算预测输出M，公式如下1-2：

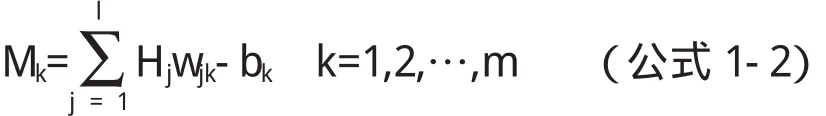
第四步：进行误差的计算.在第三步得到的网络预测输出M，与期望输出Y之间进行计算，得到的结果就是网络预测误差e.公式如下：

ek=Yk-Mkk=1,2,…,m （公式1-3）

第五步：得到的误差e以后，进行权值wij，wjk和阈值a，b的更新.更新的公式如下所示：

其中的η是BP神经网络的学习速率.

第六步：判断迭代是否结束，如果没有，则返回到第二步.

在实际学习的过程当中，η的影响是很大的，η越大，权值的变化就会剧烈.所以在应用中，在不导致振荡的前提下取可能大的η值[3].故有了BP神经网络的缺点，BP神经网络的收敛速度慢，η必须小于一个上限才能保证算法的收敛性[4]；BP神经网络所得到的网络泛化能力差，容错性能差；由于BP神经网络算法的不完备性，易陷于局部最优的情况等缺点[5].

1.2 遗传算法

遗传算法是在1962年提出[6]，在1975年，美国的Holland教授正式提出了遗传算法[7].在大自然环境中，生物有很强的适应能力和生存能力，研究者依据这个现象，并在达尔文所提出的进化论理论引导下，提出了遗传算法.遗传算法也可以说是一种随机化算法，也是一种全局优化搜索算法，该算法是基于对生物的遗传和演化过程的一种模型，参照的是生物中心法则（geneticcentraldogma）.

用遗传算法解决问题，要对复杂的问题建立合适的种群模型.从初始化种群开始，进行选择，在此过程中，是需要对每个个体进行评价，即计算每个个体的适应度，那些比较优质的个体直接遗传给下一代或者通过配对交叉，再遗传给下一代.在此遗传的过程中，可能发生变异，变异是群体中某些个体的某些基因发生了变动，与之前的本身基因不一样了，这样，种群会得到下一代的种群，这就是遗传算法的理论依据.上述过程，遗传算法有一个适应度计算，称为适应度函数，按照这个适应度函数进行种群的基本要素操作，即选择操作、交叉操作、变异操作来保留种群中优质的个体，淘汰那些适应度低的个体，这是一个循环迭代的过程，直到满足条件.运行参数是遗传算法不得不考虑的基本要素，初始化确定的参数，有群体大小M，以及遗传代数G，交叉概率Pc和变异概率Pm.

2 遗传算法优化BP神经网络

基于BP神经网络的非线性函数拟合，其中的算法流程分为三个步骤，首先进行BP神经网络的构建，在构建方面有系统建模和构建合适的BP神经网络；中间的一步是BP神经网络训练，这个过程中有BP神经网络的初始化、BP神经网络的训练以及判断训练是否结束；最后，BP神经网络的预测，测试数据和BP神经网络的预测属于该过程.遗传算法优化BP神经网络的算法流程与BP神经网络的同样分为三个流程，分别是BP神经网络结构确定和遗传算法的优化，以及BP神经网络预测.其中，BP神经网络结构的确定根据BP神经网络的输入层和输出层的参数个数，进一步，遗传算法个体长度得到确定.BP神经网络的权值和阈值，需要遗传算法优化，优化之后，每个种群个体都将包含一个网络的所有权值和阈值，在遗传算法的适应度函数的计算下，种群中个每个个体都将得到个体适应度值.选择操作、交叉操作和变异操作的遗传算法基本操作下，会找到最优适应度值所对应的个体.这样用遗传算法得到的最优个体的权值和阈值，针对BP神经网络预测初始权值和阈值赋值，神经网络经过训练后，预测函数输出拟合值将会得到.算法的流程图如图2-1：

图2-1 GA-BP神经网络算法流程图

在流程图中，可以看出，遗传算法优化BP神经网络的实质就是优化了BP神经网络的权值和阈值，从而使网络预测拟合效果更佳.遗传算法优化的过程中，有选择操作、交叉操作以及变异操作，计算适应度值的适应度函数也是优化过程中重要的一部分.之后判断是否满足条件，如果满足条件，就获取了最优权值阈值，之后进行BP神经网络的操作；否则循环做遗传算法里面的选择、交叉和变异等操作.

3 遗传算法优化BP神经网络的非线性函数拟合算法实验和比较

3.1 遗传算法优化BP神经网络非线性函数拟合算法实验

选择的非线性函数是y=x12/4+x22/9，随机生成2000组输入（x1，x2）数据和输出（y）数据，其中随机选择1900组数据作为训练数据，主要用于BP神经网络训练，测试数据是剩下100组输入输出数据，用于测试网络的拟合性能.训练好的网络用于神经网络预测函数的输出，并对预测结果进行分析.

遗传算法优化BP神经网络的构建，根据上面非线性函数特点，有两个输入参数，并有一个输出参数，从而确定了输入层的节点数是2，输出层的节点数是1.BP神经网络中隐含层的确定，如果隐含层节点数太多，BP神经网络不能建立复杂的映射关系，造成网络预测误差较大，但是如果选择的节点过少，则会造成网络学习时间增长，并且有可能出现“过拟合”现象，即训练样本预测准确，但是其他样本预测误差较大.经过实验（仅基于BP神经网络的情况），得到隐含层的节点数为5的情况，是最佳的.因此，遗传算法优化BP神经网络的结构是2—5—1结构.这样网络就有15个权值，以及6个阈值.遗传算法优化BP神经网络的参数设置，迭代次数为100次，学习率设置为0.1，训练目标值设置为0.000001（接近于最佳目标值）.遗传算法中的适应度函数用训练数据来训练BP神经网络，并且把训练数据预测误差作为个体适应度值.在遗传算法的选择操作中，采用的是轮盘赌法，从种群中选择适应度较好的个体组成新的种群.交叉操作中，随机从适应度较好的两个个体，按着设置的种群交叉概率值交叉得到新的个体.同样的变异操作是在设置的概率变异值下变异得到新个体.遗传算法的基本参数设置，进化的次数为200代，种群的规模设置为10，交叉概率值为0.3，变异概率值为0.15.

实验结果如下：

图3-1 最忧个体适应度值

如上图3-1，遗传算法优化过程中，最优个体的适应度值曲线变化图，找到最适合的，提取最优的权值阈值.得到的值如下表3-1所示：

表3-1 遗传算法优化的权值阈值

表3-1，首先的10个权值是输入层和隐含层之间的权值，第三行的5个阈值是输入层与隐含层之间的，第四行的权值是输出层与隐含层之间的，最后的一个阈值是输出层与隐含层之间产生的.利用得到最优权值阈值，赋值给BP神经网络，得到了遗传算法优化之后的BP神经网络.得到BP神经网络预测输出如图3-2和预测误差如图3-3所示.

图3-2 GA-BP网络预测输出

图3-3 GA-BP网络预测误差

3.2 与BP神经网络的非线性函数拟合的比较

BP选择的非线性函数与上述函数相同，并基于相同迭代次数、学习率以及训练目标值参数的设置，并在BP神经网络最优的2—5—1网络结构下实验.

其实验结果如图3-4和预测误差图3-5：

图3-4 BP网络预测输出

通过上述图3-2与3-3和图3-3与图3-5的比较，遗传算法优化算法的网络预测误差的精度比BP神经网络的网络预测误差的精度要精确的多，而得到遗传算法优化后的BP神经网络非线性函数拟合的效果更好，并且预测误差更加精确，在收敛速度上，遗传算法也更佳.

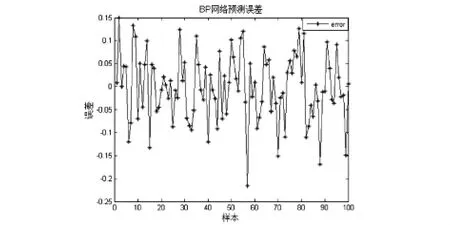
图3-5 BP网络预测误差

4 总结

遗传算法和BP神经网络都是基于生物理论的基础上做的，但是二者有着本质的区别，通过学习和实验，互相补足各自算法的缺点，提高人们对复杂问题另辟路径的方法.根据本文的研究表明，对比之前BP神经网络的非线性函数的拟合，运用遗传算法优化了权值和阈值，提高BP神经算法非线性函数的拟合的收敛速度慢，也改善了易陷于局部极小值的情况出现,有效的减少了拟合产生的误差,使得函数的拟合更加的精确,达到了较好的拟合效果.

〔1〕张燕平，张铃.机器学习理论与算法[M].科学出版社,2012.

〔2〕杨建刚.人工神经网络实用教程[M].杭州:浙江大学出版社,2001.

〔3〕王俊清.BP神经网络及其改进[J].重庆工学院学报（自然科学版），2007（03）：

〔4〕吴小培,费勤云.一种提高BP算法学习速度的有效途径 [J].安徽大学学报 (自然科学版), 1998,22(3):64-67.

〔5〕Martin R,Heinrich B.A Direct Adaptive MethodforFasterBack-propagationLearning: TheRPROPAlgorithm [A].RuspiniH.ProceedingsoftheIEEEInternationalConference OnNeuralNetworks(ICNN)[C].NewYork. 1993.586-591.

〔6〕Holland JH.Outline foralogic theory of adaptivesystems.JournaloftheAssociationfor ComputingMachinery,1962,(9):297-314.

〔7〕HollandJH.AdaptationinNaturalandArtificialSystems.Ann Arbor:TheUniversityof MichiganPress,1975.

TP301.6

A

1673-260X（2014）11-0029-04