再制造曲轴疲劳寿命分析

刘怀银， 冯国胜， 刘怀金， 高 爽

(1.石家庄铁道大学机械工程学院，河北石家庄 050043;2.山东能源枣庄矿业(集团)有限责任公司铁路运输处，山东枣庄 277000)

曲轴是发动机中最重要、承载最复杂、价格较昂贵的零件之一，对曲轴进行绿色再制造是发展循环经济和构建节约型社会的重要途径之一。产品再制造的可行性和可行度是发展再制造产业首要面临的问题，对再制造曲轴进行强度分析及疲劳寿命的评估是一项重要的工作［1-2］。现主要是对某工程机械发动机再制造曲轴进行应力和疲劳寿命进行分析，提出了再制造曲轴建立有限元模型的方法，得出原始曲轴与再制造曲轴仿真出疲劳寿命的结果是相同的，为曲轴的再制造提供模拟仿真结果，减少了实验工作量，这样既可以节约成本，又为曲轴的再制造提供了理论依据。

1 有限元模型的建立及计算

1.1 曲轴三维实体模型

利用三维建模软件PROE对某工程机械六缸四冲程柴油发动机曲轴进行实体建模。曲轴的主要设计参数为:连杆轴颈直径为79.375 mm，连杆轴颈圆弧半径为4.953 mm，主轴颈直径为115.06 mm，主轴颈圆弧半径为4.953 mm，油孔直径为7.925 mm，曲轴的总长为1 299.413 2 mm。曲轴材料为42CrMoA，曲轴涂镀层材料为3Cr13。因为再制造的曲轴有两种材料组成，在有限元软件MSC.PATRAN下对第一种模型进行改进，就可得到第二种模型即再制造曲轴模型。

1.1.1 原始曲轴的有限元模型

把已经在三维建模软件PROE中建立的曲轴模型导入MSC.PATRAN有限元软件中，在PROE软件中把曲轴模型保存成x_t格式导入即可。对完整的曲轴模型不需要进行任何处理，然后对其划分网格即可，这里采用四面体四节点实体单元，整体曲轴有限元模型划分为159 951个节点，801 138个单元。由于曲轴受到的载荷很大，各部位应力分布不是很均匀，局部有应力集中，所以对应力集中区网格进行细化，根据以往经验应力集中主要出现在连杆轴颈与曲柄臂过渡圆角处，这也是曲轴经常发生疲劳破坏的地方。整体曲轴的有限元模型如图1。

1.1.2 再制造曲轴的有限元模型

再制造曲轴是在原始曲轴磨损后，先把所有主轴颈和连杆轴颈磨削1 mm，然后再喷涂1 mm厚的3Cr13，这样可以保证再制造曲轴和原始曲轴的尺寸参数相同。对涂镀层赋予shell单元属性，采用体单元和壳单元结合体。对于两种尺寸相差很大的实体，使用如下方法可以完成建模。

在PROE软件中建立原始曲轴模型，直接导入MSC.PATRAN中，第一步对其进行划分网格，在这里采用的四面体四节点实体单元，整体曲轴有限元模型划分为159 951个节点，801 138个单元。根据实际情况对应力较大的区域进行网格细化。

第二步在划分完网格的有限元模型中，为保证曲轴划分网格后节点与涂镀层的节点能够很好的结合，在PATRAN软件meshing菜单下面，创建element，单元形状为tri，然后选择只显示整个单元体的最外面那层单元visible entities only命令。因曲轴磨损主要发生在主轴颈和连杆轴颈上，故再制造时对曲轴的这两个部位实施喷涂工艺。可以直接选择主轴颈和连杆轴颈最外面的那层单元，在选择单元的过程中可能会误选上其他面上的单元，可以使用plot/earse命令显示你所创建的单元，在显示你所创建的单元之前，必须要记录下来你所创建单元的数量及编号，这样就可以在plot/earse命令里面修改你所需要的单元。

第三步，修改完单元之后如图2，然后再给其涂镀层赋予shell单元属性。因为在这里选择的最外层单元是属于曲轴划分完网格之后的单元，也就是赋予shell属性之后涂镀层单元从最外面那层面单元往里面“渗入”1 mm的厚度，所以对其进行的选择能保证其节点很好的结合在一起，就不会出现最外层单元在计算之后的翘曲现象。因曲轴为六缸曲轴，所以选择之后是13个圆柱环。

图2 涂镀层的网格

图1 整体曲轴有限元模型

1.2 载荷状况的确定

作用于曲柄连杆机构的力分为:缸内气压力，运动质量的惯性力、摩擦阻力和作用在发动机曲轴上的负载阻力。根据计算公式在MATLAB编程后，将某工程机械发动机的有关设计参数代入(这里取转速1 500 r/min)计算出的曲柄销负荷图，由于发动机进气和排气过程，气缸内所受压力较低，在这里只对发动机的压缩和膨胀过程进行分析，所得发动机力特性如图3所示。图3中* 为合力，－往复惯性力，+为气缸压力(Pa)。

曲轴在工作时承受缸内的气体压力、往复和旋转质量惯性力的作用，根据发动机动力学计算，求得此发动机连杆轴颈载荷的最大值，及随后曲轴再转过 120°、240°、360°、480°、600°时连杆轴颈载荷的数值［3］，见表1。

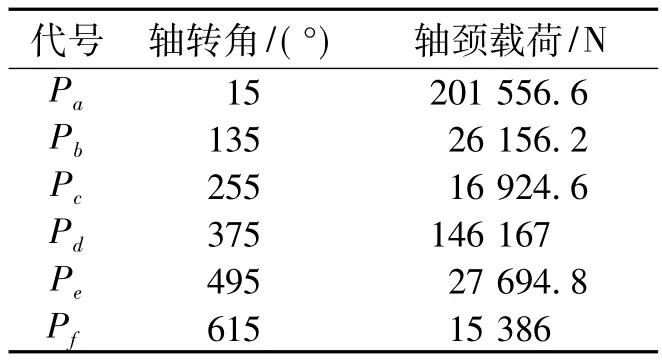
表1 发动机曲轴连杆轴颈载荷

1.3 力的边界条件

根据传统的方法及有限宽度轴颈油膜压力应力分布规律，并忽略油孔处压力峰值突变的影响，假定力边界条件为:载荷沿连杆轴颈和主轴颈轴线方向按二次抛物线规律分布;沿轴颈圆周120°角范围内按余弦规律分布［4-5］。曲轴的在进行计算时力的边界条件采用的如下方法［6］:设连杆轴瓦有效宽度为2L，并设在曲轴纵向对称面内半连杆轴颈有效宽度上沿轴向有n个等距节点，如图4。

载荷沿轴向的抛物线分布，则

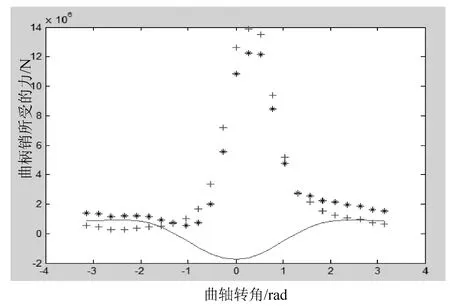
图3 发动机的力特性图

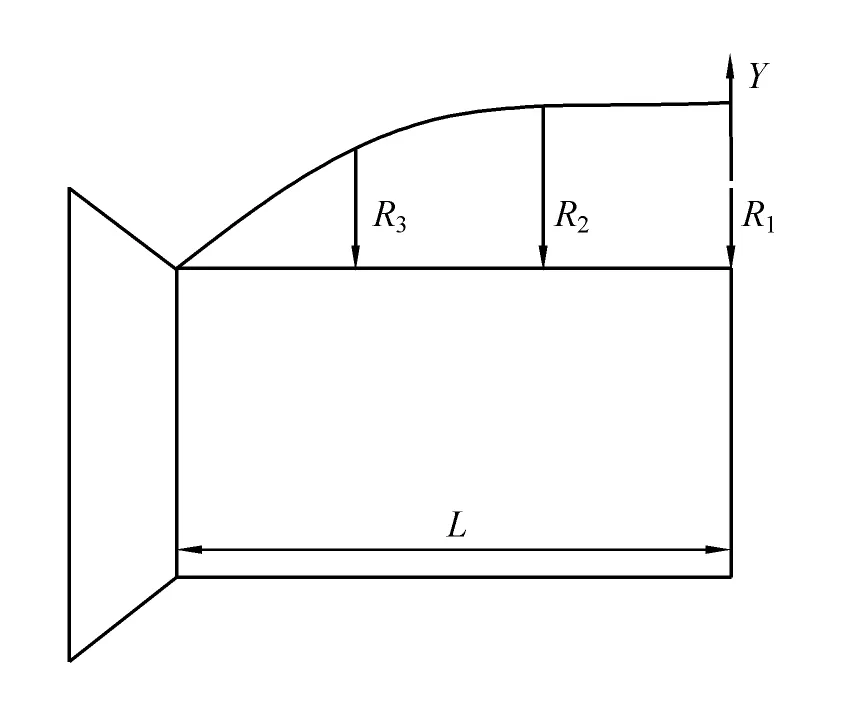
图4 轴向抛物线分布

这样，可以得出各节点的载荷值，采用的是三节点也就是n=3的情况，则有

式中，R1、R2、R3为作用在轴瓦上的力，Pa为作用在连杆轴颈上总载荷。考虑到连杆轴颈上载荷的对称性，在进行强度计算时在节点处R1应取R1/2而不是R1，其余各处的R值不变。曲轴约束的边界条件可以设置成把UX、UY、UZ三个自由度都约束住，因为只进行静应力分析。

对曲轴施加的力是沿Y轴方向的力，通过分析比较三缸发火时所受的应力最大，受力情况如图5所示。Pa到Pf分别为三缸、五缸、一缸、四缸、二缸、六缸所受的力。

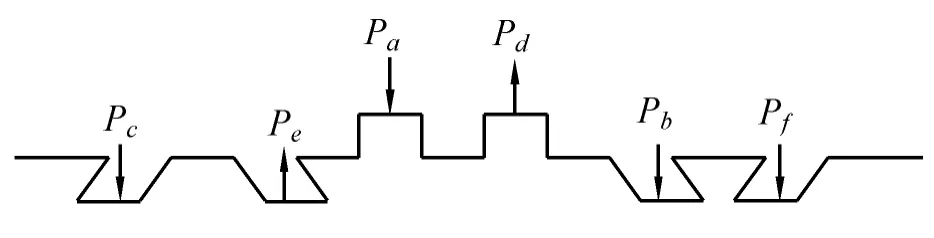
图5 曲轴三缸发火各缸受力图

1.4 支撑边界条件

除了考虑曲轴的边界约束外，还得考虑到曲轴的主轴颈上的约束，因为主轴颈座在轴承座上。将主轴承对曲轴的支撑视为弹性支座，即设定其弹性刚度，根据查阅的相关资料认为其弹性刚度值在曲轴纵向对称面内沿主轴颈轴向分布［7］。在每个主轴颈下面建立两个点，然后在其点上创建节点node，然后在创建element单元，就是建立的两个节点与主轴颈上的与之相垂直的节点进行连接，给其设定1维spring，即为所需要的弹簧单元。

为了防止曲轴沿轴向产生刚体位移，将其左端纵向对称面上靠近轴心的两个结点Z向位移取为零。显然这种边界条件的取值是接近实际情况的。

1.5 结果分析

由于原始曲轴和再制造曲轴所受的力边界条件、载荷边界条件和支撑边界条件都是相同的，所以不再详细叙述再制造曲轴的工况条件。

1.5.1 应变分析

仿真计算结果表明，在3缸发火时，两种工况的变形量最大分别为1.16 mm和1.35 mm，发生在三、四连杆轴颈及第一曲柄臂处。位移变形图如图分别为6和图7所示。

1.5.2 应力分析

在三缸发火时曲轴所受应力是最大的，经计算完整曲轴最大应力点在第三连杆轴颈右侧与曲柄臂的过渡圆角区域，最大值为644 MPa。曲轴第三连杆轴颈左侧应力值为601 MPa。其余部位应力值较小。同理，在制造曲轴的最大应力点第三连杆轴颈右侧与曲柄臂的过渡圆角区域，最大值为549 MPa。曲轴第三连杆轴颈左侧应力值为588 MPa。两种曲轴的应力云图如图8和图9所示(由于曲轴形状是空间相差120°，所以所加载的力只有三、五缸的力比较清晰，其他的由于角度问题所以显示不出来力的加载。)。

图6 原始曲轴位移变形图

图7 再制造曲轴的位移变形图

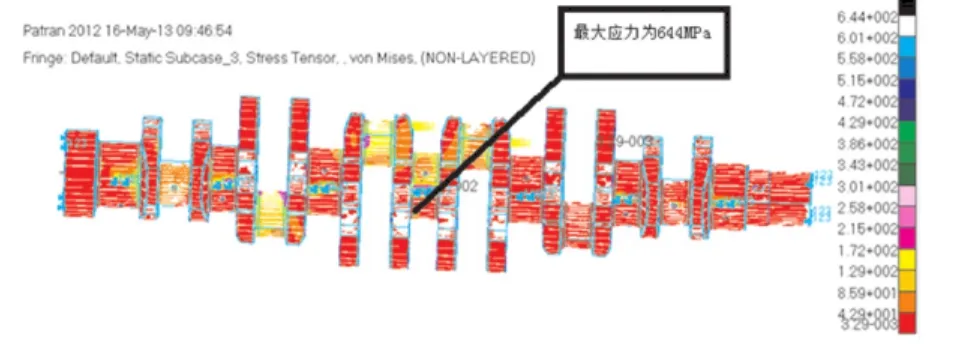
图8 原始曲轴的应力云图

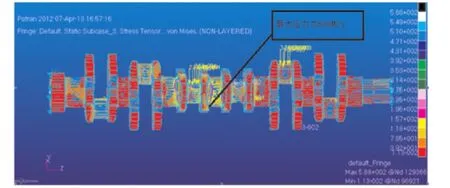
图9 再制造曲轴的应力云图

2 疲劳寿命分析

疲劳计算时是要静力的应力水平再乘以载荷谱，然后再计算疲劳寿命，所有疲劳寿命不仅和静力的应力水平有关，还和载荷谱有关，曲轴属于高周疲劳。

运用机械系统仿真软件ADAMS的ENGINE模块，通过建立包括活塞、连杆、曲轴、飞轮在内的整个曲轴系的多体系统动力学模型，可以计算出各构件的运动规律和构件间的作用力，为曲轴有限元分析力边界条件和时间载荷历程曲线的确定提供基础。依据提供的活塞、连杆、曲轴、飞轮等图纸就可以生成发动机的曲轴连杆活塞实体模型，如图10所示。通过ADAMS动力学仿真可得出曲轴的时间载荷历程曲线，如图11所示。

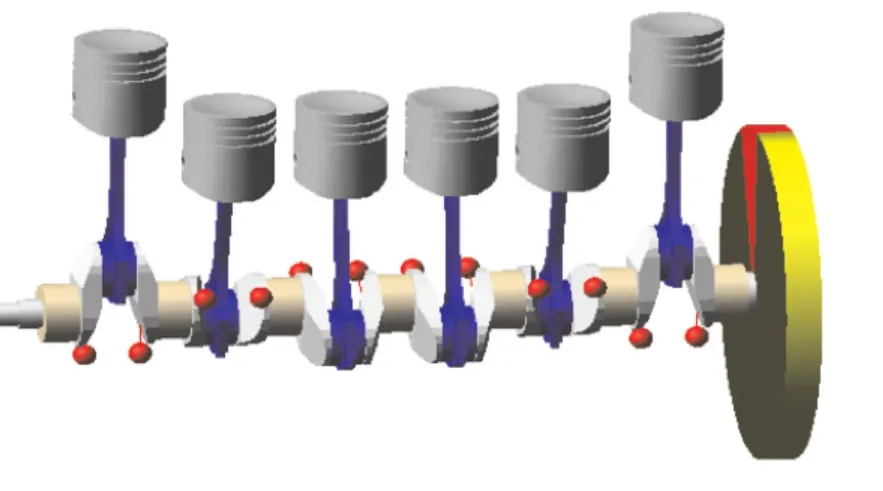
图10 发动机的曲轴连杆活塞实体模型

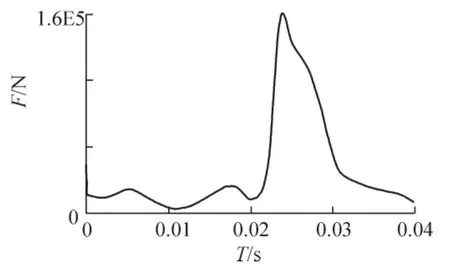
图11 曲轴时间载荷历程曲线

由此可以把在PATRAN中得到的静应力结果导入MSC.Fatigue软件中，与时间载荷历程相关联之后计算出，曲轴对应各种工况下的疲劳寿命，并且可以得出大部分节点的疲劳寿命，从而可以估算整个曲轴的疲劳寿命。完整曲轴最小寿命节点是138 777，再制造曲轴的最小寿命节点为122 707。两种曲轴的疲劳寿命云图如图12和图13。图中－9.700为以10为底的对数值。采用对数方式显示寿命结果时有利于结果底插值表示［8］。

原始曲轴与再制造曲轴静强度和疲劳强度仿真结果如表2。

表2 各种工况条件下仿真结果比较表

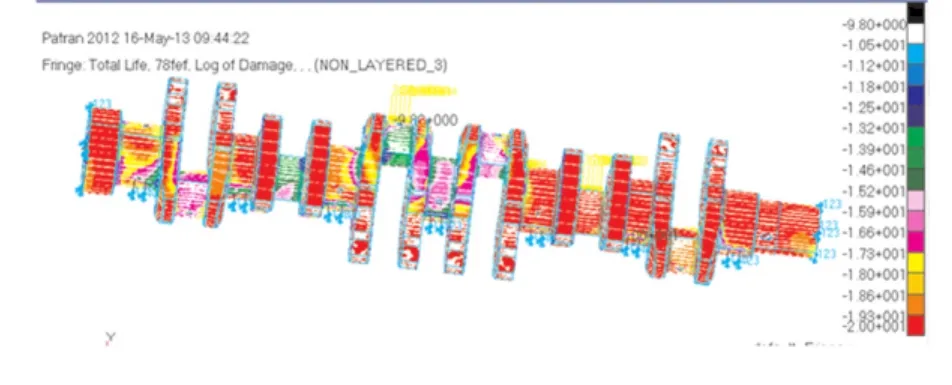
图12 原始曲轴疲劳寿命云图

图13 再制造曲轴疲劳寿命云图

由表2可以看出，原始曲轴最小寿命为6.28E9，再制造曲轴所对应的最小寿命为5.064 7E9。由以上两种情况计算出的应力，以及在MSC.Fatigue软件中计算出的疲劳寿命可知，应力最大位置在油孔处以及连杆轴颈过渡圆角处，在这些地方容易破坏并且疲劳寿命相对来说较低。

3 结论

通过对原始曲轴和再制造曲轴静强度和疲劳寿命的仿真分析结果比较，可以看出，两种情况的下的疲劳寿命最小的位置就是出现在所计算出的应力最大的位置。对原始曲轴和再制造曲轴进行了静强度和疲劳强度分析，从仿真结果可知，再制造曲轴具有较高的疲劳寿命。

［1］张国庆.零件剩余疲劳寿命预测方法与产品可再制造性评估研究［D］.上海:上海交通大学机械与动力工程学院，2007.

［2］黄邦戈，陆宇衡;，谢德锦.发动机曲轴再制造工艺研究［J］.装备制造技术，2011(5):10-12.

［3］冯国胜，杨绍普.车辆现代设计方法［M］.北京:科学出版社，2006.

［4］尹建民，五德海，袁银海，等.X6135柴油机曲轴强度的三维有限元研究［J］.内燃机工程，1997，18(2):71-77.

［5］邓江华，冯国胜.柴油机曲轴的静、动态有限元分析及校核［J］.石家庄铁道学院学报，2005，18(1):58-61.

［6］庞永，刘君德.发动机曲轴应力的有限元分析［C］//中国力学学会93 SAP5/SAP5P年会论文集.北京:中国力学学会，1993:36-51.

［7］孙军，桂长林，汪景峰.边界条件处理对曲轴有限元分析的影响研究［J］.汽车工程，2005，27(6):724-726.

［8］王国军.Msc.Fatigue疲劳分析实例指导教程［M］.北京:机械工业出版社，2009.