齿式橡胶联轴器动力力学建模与分析

王 海， 温建明

(同济大学航空航天与力学学院，上海 200092)

0 引言

联轴器是用来联接两轴或轴和回转件的一种机械传动部件，根据是否引入弹性元件，可分为刚性联轴器和弹性联轴器。弹性联轴器具有能产生一定的弹性变形和阻尼作用的弹性元件，不但能补偿两轴间的相对位移，还能起缓冲和减振作用［1］。

目前，分析联轴器减振性能主要采用基于线刚度和黏性阻尼系数的线性模型，文献［1］中详细论述了该模型下弹性联轴器在简谐载荷和冲击载荷作用下的动力特性计算。针对弹性联轴器的非线性特点，马建敏以弹性联轴器联接的两转子系统为研究对象，分别讨论了联轴器非线性刚度、非线性阻尼对系统在冲击荷载下扭振响应的影响［2-3］。而在弹性联轴器数学建模方面，龚宪生针对船舶用钢丝绳弹性联轴器进行一系列的工作［4-6］，采用拟合分解法以及阻尼等效原理对大挠度弹性联轴器振动试验数据进行处理，建立了一个与振动位移幅值有关的非线性迟滞恢复力数学模型。左时伦在对联轴器进行动态试验所得数据的基础上导出了联轴器动态刚度的一个定量公式，公式表明动态刚度是平均转矩的强函数，动态刚度并非振动频率的强函数［7］。

在前人研究的基础上，采用有限元技术和理论分析相结合的方法，建立了一款齿式橡胶弹性联轴器恢复力模型，进而建立联轴器轴系的动力学方程，分析了联轴器的幅频特性以及扭矩传递系数。

1 联轴器橡胶元件的有限元分析

图1是工程中常用的一款HRC 150橡胶联轴器，因是一循环对称结构，可以选取对称单元来分析。为简化计算，有限元分析最终采用图2所示模型，图2中1号、2号是橡胶片，尺寸都为(44×40×10)mm3，密度为1 650 kg/m3，3、4 号和 5 号是刚性片。

考虑到橡胶加入了炭黑和工作于有限变形状态，其松弛率并非与应力成正比，选用J.S.Bergstrom和M.C.Boyce提出的现象学本构模型来模拟橡胶材料有限变形时的时间依赖特性，在Abaqus中该模型以关键词*Hyperelastic和*Hysteresis定义。

超弹模型(Hyperelastic)选用Arruda-Boyce模型

图1 HRC 150联轴器

图2 橡胶元件有限元计算模型

迟滞模型(Hysteresis)Arruda-Boyce模型中取参数 μ =0.6 MPa，迟滞模型取参数 B=0.555 6 MPa－4s－1，m=4.0，n=－0.1;此外，迟滞模型还需用参数S来定义超弹模型和迟滞模型中瞬时弹性力比率，取S=1.6。分析程序选用Dynamic，上下边界固定，中间边界施加简谐位移激励s=Asin(2πωt)，幅值 A 分别取 0.2、0.4、0.6、0.8、1.0 和 1.2 mm，频率 ω 取 15、20、25、30、50、70、100 和 150 Hz，共 48 个载荷，可以满足联轴器工作时最大变形和最高频率的要求。有限元分析采用C3D8R单元，把中间边界上参考点的y方向节点力作为时间变量(History Output)输出。分别提取各工况下Abaqus计算的恢复力、位移数据，得到滞回曲线如图3所示。

图3 橡胶元件的迟滞回线图

相比于通过对橡胶弹性联轴器进行实验来建立其恢复力数学模型，有限元方法只需对橡胶材料的标准件进行实验，得到材料本构的参数即可，周期短，代价小，并且，模型修改起来也很方便，针对大量不同类型的联轴器分析更具优势。

图4 恢复力分解为非迟滞力和迟滞力

2 橡胶元件力学模型的建立

橡胶弹性元件的迟滞恢复力-位移曲线关于原点对称，由上下两条组成，并与速度有关，即

如图4，可以把迟滞回线分解为关于原点对称的幂函数曲线和以原点为中心的椭圆函数曲线的叠加。

幂函数曲线fk=(fU+fL)/2，表示非迟滞力;类椭圆函数曲线fk=(fU－fL)/2(上支)、fk=(fL－fU)/2(下支)，表示纯迟滞力。由于分解出的幂函数曲线随位移的变化规律接近线性，采用fk=k(A，ω)x来拟合，阻尼力采用等效阻尼形式fc=c(A，ω)˙x，这里的刚度系数和阻尼系数是振幅A和频率ω的函数。最终，采用最小二乘法拟合得到橡胶元件的恢复力数学模型为

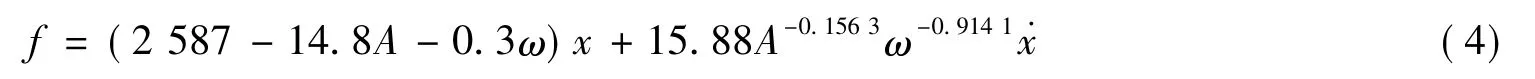
由经拟合得到的恢复力函数关系式重构滞回曲线，并与原滞回曲线画在同一坐标系下如图5，可见两者有很好的一致性。

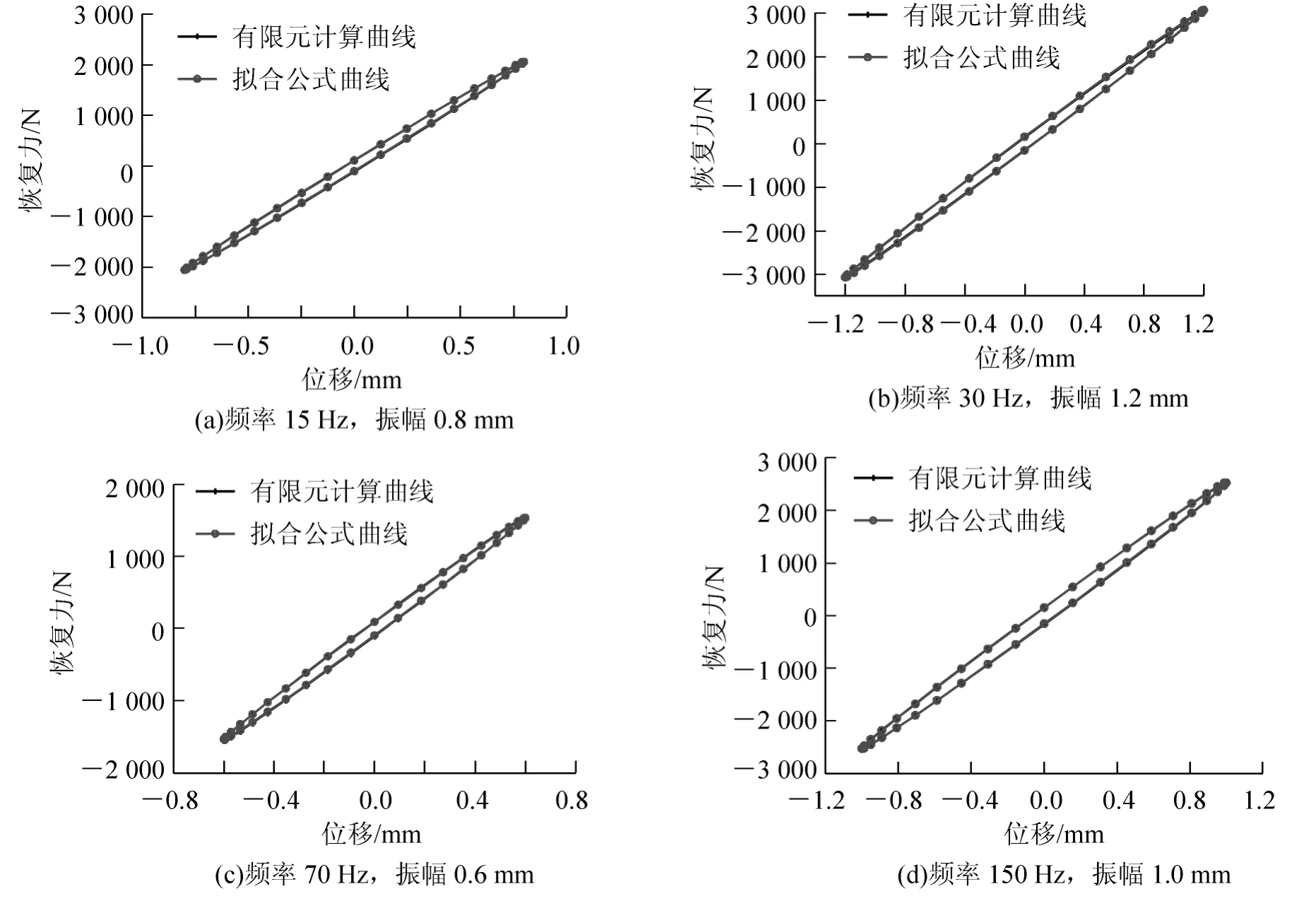
图5 原迟滞回线和重构迟滞回线

3 联轴器幅频、相频特性分析

对于分析的HRC 150联轴器，橡胶元件共有3对，橡胶元件到轴心的平均半径R=53 cm。令φ为两半联轴器的转角差，φ0、ω为稳态时转角差的幅值和频率，则橡胶联轴器的恢复扭矩

设定主动端(转动惯量J1)以恒扭矩M1经联轴器带动从动端(J2)，从动端扭矩M2=M1+M0sin(2πωt)，有一简谐规律变化的扰动扭矩分量M0sin(2πωt);转角分别为φ1、φ2，如图6所示。动力学方程

图6 联轴器动力特性计算简图

由式(6)×J2－式(7)×J1，得

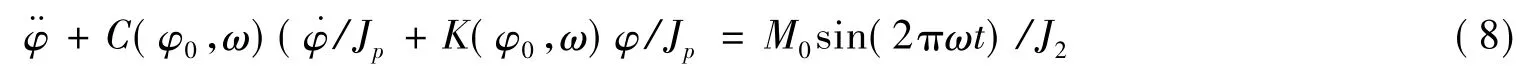
式中，Jp=J1J2/(J1+J2))。令稳态解为:φ = φ0sin(2πωt+ θ) ，代入式(8)，得

式中，φ0为转角差幅值，θ为相位差。取J1=J2=18(t·mm2)，代入式(9)和式(10)得幅频特性曲线ω－φ0如图7所示。

从幅频特性曲线图中可以看出，联轴器在传递扭矩的过程中相当于与一个非线性软弹簧，在补偿轴系的相对位移的同时可以减小轴系的振动，并且随着简谐扭矩的幅值增大，软弹簧特性越加明显。由于联轴器的主要作用是传递扭矩，因此扭矩的传递效率也是工程中关心的一个问题。

联轴器传递的变动扭矩

传递的变动扭矩最大值

动力放大系数

橡胶块传递的总扭矩

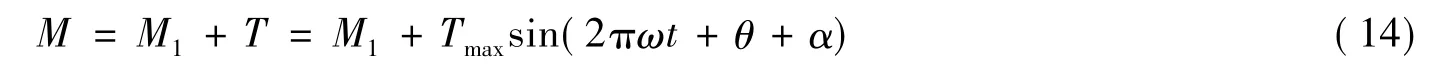
当取M0=1×104N·mm，M1=2×104N·mm，扭矩传递系数

图7 幅频特性曲线图

图8 扭矩传递系数峰值

4 结论

通过对联轴器的橡胶弹性元件进行正弦激励有限元分析，得到了橡胶元件的滞回曲线。根据滞回曲线的特点，联轴器的恢复力模型采用刚度系数、阻尼系数关于振幅和频率的函数来表述，并识别出了相应的系数。结果表明，重构的恢复力-位移曲线和原数据有很好的一致性。在选定的频率范围，联轴器的动态刚度随频率的变化略有减小，与文献［7］有类似的结论。最后对联轴器的幅频曲线以及传递系数进行了分析，发现联轴器类似于一个非线性软弹簧，存在有一不稳定的频率区间，选用联轴器时应当避免设计工作频率处于该区间;而在具有稳定性的频率范围内，联轴器不仅具有良好的减振效果，扭矩传递系数也很接近于1，能够很好地传递扭矩。

［1］施高义，唐金松，喻怀正，等.联轴器［M］.北京:机械工业出版社，1988:90-102.

［2］马建敏，韩平畴.柔性联轴器刚度非线性对扭转振动的影响［J］.振动与冲击，2005，24(4):6-8.

［3］马建敏，杨万东.柔性联轴器非线性阻尼对扭转减振的影响［J］.振动与冲击，2005，25(3):11-13.

［4］龚宪生，赵玫.具有非线性迟滞特性的大挠度弹性联轴器建模［J］.上海交通大学学报制，1995，29(3):49-54.

［5］龚宪生，赵玫.大挠度弹性联轴器的阻尼耗能特性、建模及参数识别［J］.机械强度，1996，18(2):11-12.

［6］龚宪生，赵玫.一种全新矿用高弹性联轴器动态性能的研究［J］.煤炭学报，2001，26(4):418-423.

［7］左时伦.弹性联轴器动态刚度的数学建模与试验研究［J］.煤矿机械，2011，32(3):82-84.