客运专线32 m双线整孔简支箱梁张拉应力试验研究

李士元

(中铁十二局集团第三工程有限公司，山西太原 030024)

在高速铁路建设中大量采用了以桥代路，桥梁比例已达到线路总长度的70% ～80%，其中90%为预应力混凝土简支梁。高速铁路对轨道的平顺性要求很高，不但要求轨道精调后的标高符合设计要求，而且对运营期的徐变上拱度进行严格控制。在常规设计计算时，通常用初等梁弯曲理论计算预应力梁沿梁高的应力分布，但箱梁顶板、底板的剪力滞效应不能用初等梁理论计算，这样在设计的预加力作用下，结构的实际工作状态可能与常规设计计算结果偏差较大，通常会对运营期结构的徐变上拱度控制产生不利影响［1］。另外，预应力是通过锚固来建立的，在锚固处，从施力处到等于一个梁高的距离内，是一个应力过渡区段。这个区段内的应力处于多向应力状态，也不能用初等梁弯曲理论求解。一般这段应力过渡区称为“端块”［2］。通过实测可以了解端块内应力的分布情况，掌握横向拉应力的大小，以便于控制其数值，为同类设计积累经验数据。因此，测试客运专线32 m双线整孔简支箱梁的张拉应力，验证预应力设计的可靠性是设计师密切关注的课题之一。

为了掌握客运专线32 m双线整孔简支箱梁在预应力张拉后的压应力储备情况，检验其施工质量及设计的安全性，进行了现场张拉应力测试。初等梁弯曲理论虽然能计算梁截面的弯曲应力沿梁高的分布，但不能反映箱梁顶板的剪力滞效应和梁端部锚块的局部应力，故借助ANSYS软件对其进行有限元三维建模得到精确的应力分布，并将试验结果、初等梁弯曲理论计算值与ANSYS计算值进行比较分析。

1 工程概况

某客运专线上32 m双线整孔单箱单室等高度预应力混凝土箱型简支梁，梁高2.96 m，顶板宽12.0 m，箱底宽5.5 m，梁长32.60 m。该箱梁的设计荷载为ZK标准活载，混凝土标号为C50。钢绞线采用标准型高强度低松弛钢绞线:1*7Φ15.2-1860-GB/T5224—2003。预应力束采用两端同步张拉，并左右对称进行。一孔箱梁共布置27束(图1)，其中除N1a、N3、N5、N8和N10为12根钢绞线，其余均为每束13根钢绞线，基本数据如表1所示。

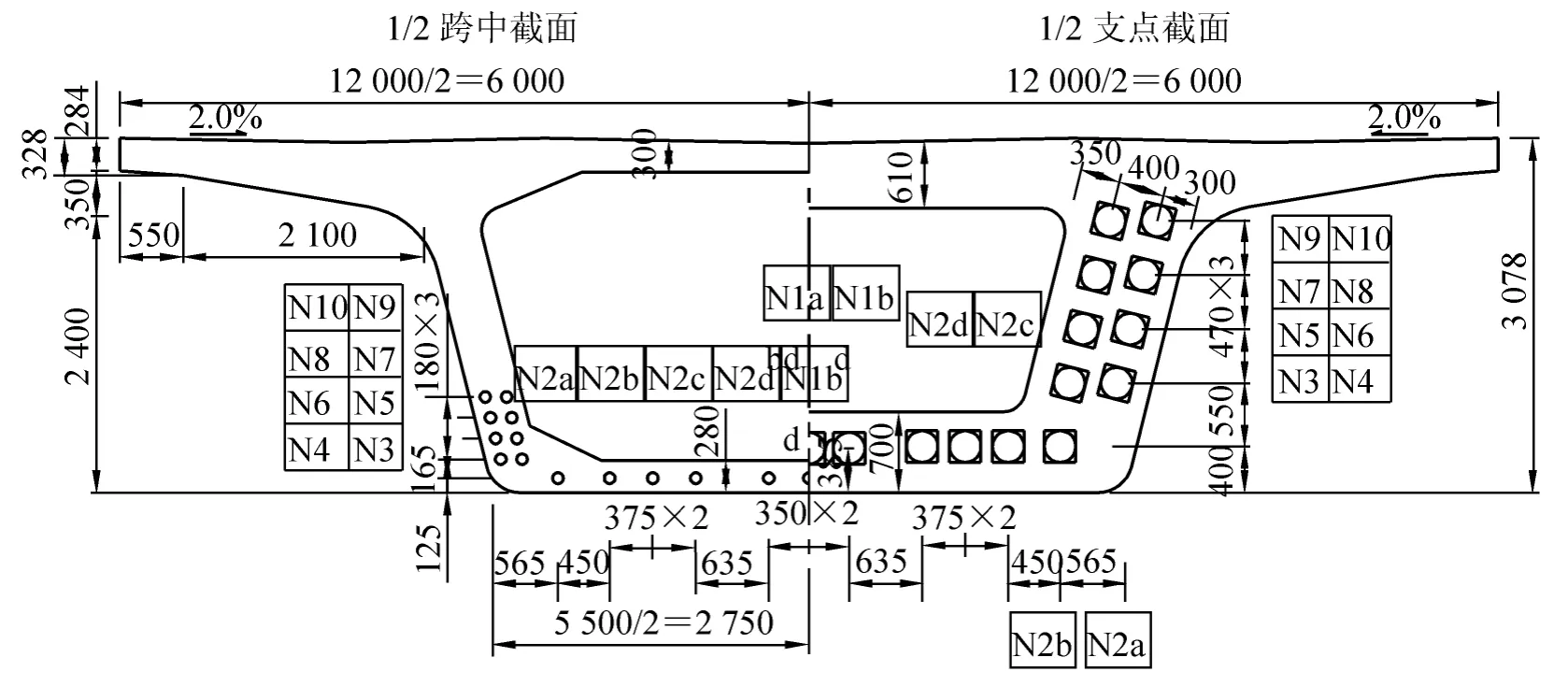
图1 32 m梁截面预应力布置图(单位:mm)

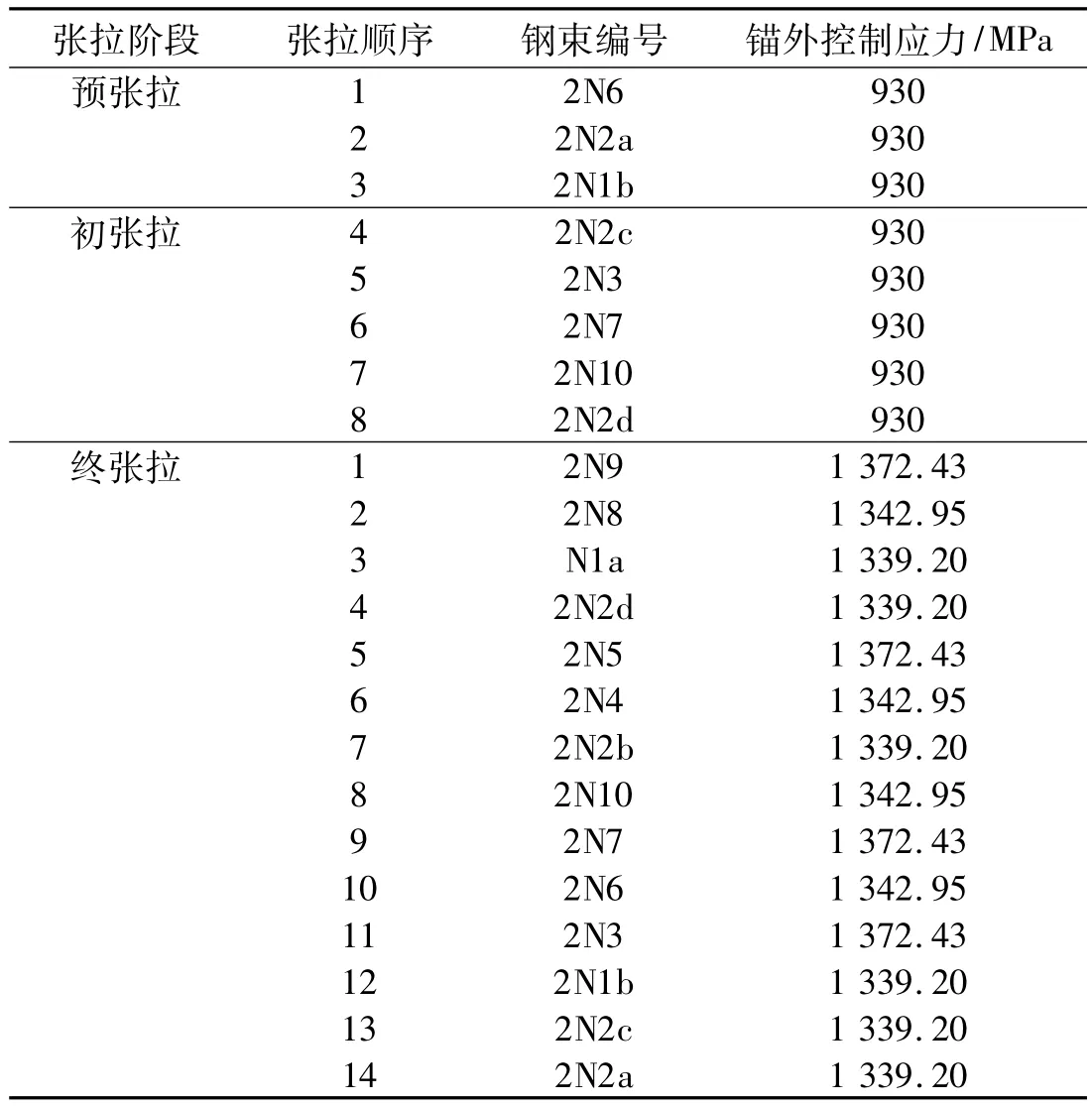
表1 预应力筋张拉顺序及控制应力

2 试验研究方案

为测试跨中截面张拉后32 m整体箱梁在预应力和自重荷载作用下的应力分布情况，掌握箱梁在预应力张拉后的压应力储备，在梁跨中截面顺桥向布置16个钢弦传感器，在与1/4断面布置9个钢弦传感器，如图2所示。传感器按预定的测试方向固定在主筋上，测试导线引至混凝土表面。

为了更好地了解在预应力集中荷载作用下混凝土局部承压区的横向应力分布情况，在锚下局部承压区沿腹板内侧横向布置了三排竖向钢弦传感器，每排3个，中心与预应力筋中心一致，共布置有9个钢弦传感器，具体布置如图3所示。采集设备采用DH3815应变数据采集仪，每张拉一束前后都进行采集，采用增量计算。

3 有限元分析

3.1 计算模型

图2 测点布置图(单位:cm)

采用通用有限元软件ANSYS按照实际尺寸建模［3］，坐标系的选取如图4所示，考虑到计算的准确性，采用分离式计算模型，即钢绞线用Link8单元模拟，而混凝土采用Solid95模拟。将混凝土和力筋划分为不同的单元一起考虑，而模拟预应力可以采用初应变法，可以模拟力筋的摩擦损失。该梁采用在移动模架造桥机上现场浇筑，梁体管道采用金属波纹管成孔，设计摩阻系数μ=0.23，管道偏差系数k=0.002 5。为精确考虑预应力摩阻损失，通过现场测试确定出实际的摩阻系数μ=0.310 9和管道偏差系数k=0.003 36，按实测的μ与k计算预应力孔道摩阻。

图3 端块横向拉应力测点布置(单位:cm)

图4 箱梁有限元模型

3.2 计算结果

利用ANSYS的path操作可得到腹板任意断面沿高度的应力分布，可列出不同路径的应力分布情况，图5、图6分别为纵向初张、终张应力分布云图。最内排处端块横向应力分布如图7所示。

图5 纵向初张应力分布云图

图6 纵向终张应力分布云图

图7 最内排钢弦横向应力分布云图

4 试验与计算结果的对比分析

试验结果和计算结果的比较如表2、表3所示，表2、表3中初张时的应力为在预应力初张荷载和混凝土箱梁自重共同作用下产生的，终张时的应力为在终张时的张拉力增量产生的应力增量。

表2 跨中截面应力对比 MPa

4.1 底板下缘应力分布

跨中底板实测和计算应力分布如图8所示。

从图8可以看出:ANSYS计算平均应力与实测平均应力的最大误差为1%，说明计算和实测都比较可靠。用初等梁理论计算的底板应力为14.5 MPa，与实测均值的误差为3.2%，与有限元均值的误差为1.4%，说明用初等梁理论计算底板下缘应力是可行的。

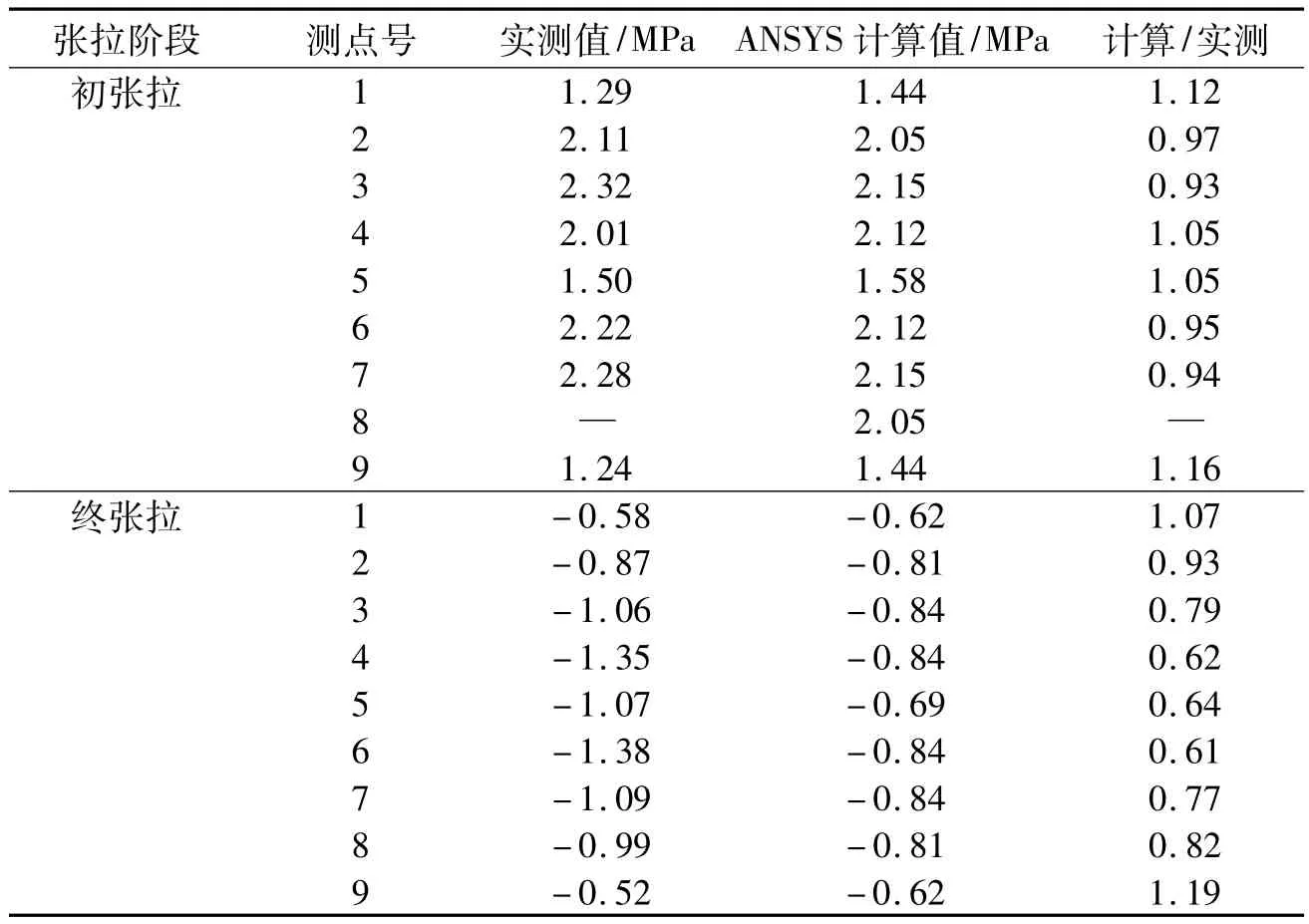
表3 1/4截面实测值与数值计算值的比较

4.2 腹板应力分布

跨中腹板实测应力沿梁高分布分别如图9所示。从表1和图9可以看出:跨中截面腹板应力沿截面高度分布的线性相关系数为0.994 8，截面应力沿截面呈良好的线性分布，说明截面变形基本符合平截面假定;实测结果与有限元计算结果随着应力数值的减小，误差略有增大，其原因是当数值较小时，钢弦传感器测试引起的误差较大。

图8 跨中底板应力分布

图9 跨中腹板实测应力沿梁高分布

4.3 顶板应力分布

1/4截面顶板应力分布如图10所示。由图10可以看出，箱梁顶板具有明显的剪力滞后效应，初等梁弯曲理论无法反映剪力滞效应，用ANSYS建立实体模型的分析结果可以反映剪力滞效应，但理论分析与实测值误差较大，其原因是顶板应力数值较小，钢弦传感器测试引起的误差较大，实测应力普遍较有限元计算值偏小，说明结构具有较大的刚度。

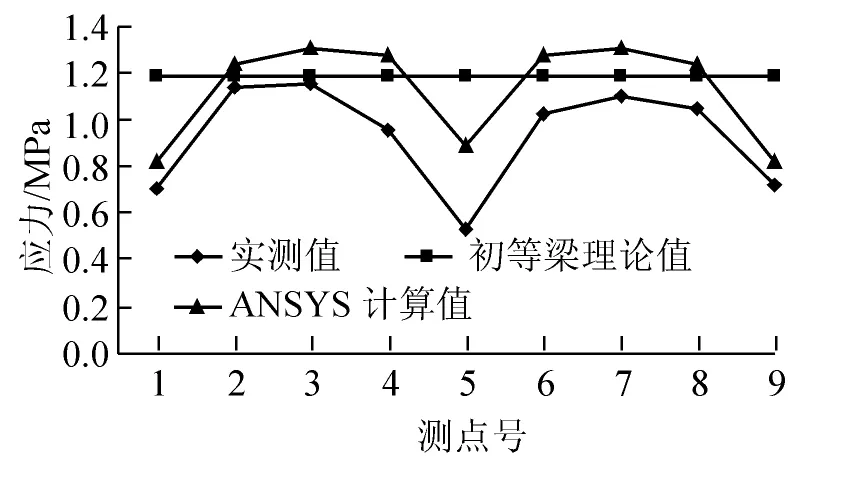
图10 1/4截面顶板应力分布

4.4 端块横向应力分布

端块横向应力实测与计算值的比较见表4。表4中初张时的应力为在预应力初张荷载和混凝土箱梁自重共同作用下产生的，终张时的应力为在终张时的张拉力增量产生的应力增量。

表4 端块横向应力实测值与计算值比较

从图7～图9和表4可以看出:

(1)计算最大横向拉应力为0.74 MPa，实测最大横向拉应力为0.87 MPa，小于规范规定值0.7×3.10=2.17 MPa，实测中也未发现开裂现象。

(2)测试和计算大部分结果吻合较好，基本规律一致。

(3)无论实测或是有限元分析，结果都表明，端块的纵向应力和横向应力分布都比较复杂，尤其是锚头比较分散布置时，这种情况更加突出。所以对于端块的应力计算，应该采用大型有限元软件进行详细的分析，传统的计算手段是无法完成的。

5 结语

由试验结果及计算分析可知，在预应力荷载作用下，底板实测应力与理论分析结果一致，实测与ANSYS有限元分析的平均应力误差在1%之内，而与初等梁理论的误差为3%，腹板实测应力分布符合平截面假定，顶板应力实测值与理论分析误差较大，其原因与顶板应力的绝对值较小有关，说明用初等梁理论进行预加力阶段计算是可行的;但不能反映箱梁顶板的剪力滞效应，ANSYS实体有限元计算弥补了初等梁理论计算的不足，可比较准确地分析整个结构的应力状态，对箱梁顶板的剪力滞效应、端块的局部应力分析不失为一种有效的工具和手段，其结果可用于指导设计和施工。

［1］李军，范超远，杨基好，等.客运专线32 m箱梁徐变效应研究［J］.石家庄铁道大学学报:自然科学版，2012，25(3):42-47.

［2］肖飞.大跨度预应力混凝土简支箱梁的梁端应力分析［J］.铁道标准设计，2004，8:78-80.

［3］王新敏.ANSYS工程结构数值分析［M］.北京:人民交通出版社，2007.