基于位置服务中半可信用户的位置隐私保护方法

吴 雷， 潘 晓， 彭志平

(1.石家庄铁道大学 经济管理学院，河北 石家庄 050043;2.石家庄铁路运输学院基础教学系，河北 石家庄 050043)

0 引言

伴随着移动计算技术和无限设备的蓬勃发展，基于位置服务LBS中的位置隐私保护研究受到了学术界的广泛关注。为保护位置隐私，Gruteser等人提出了位置K－匿名模型［1］。为满足位置K－匿名，用户的确切位置被扩展为一个匿名区域，使得区域中至少包含K个用户。后来出现了很多基于位置K－匿名的工作。可以分为两个方向:第一，如何修正位置K－匿名模型并根据用户隐私需求快速寻找匿名集［2－4］;第二，如何高效回答感知位置隐私的位置查询(如最近邻查询和范围查询)［5］。本文关注的是第一个方向。

位置K－匿名模型是大众普遍接受的位置隐私保护模型。为满足该模型，采用降低用户位置时空粒度的方法。为达到此目的，大部分现有方法均假设存在一个可信实体，网络中的所有用户向该实体发送真实位置。可信实体根据接收到的真实位置为查询请求用户寻找位置邻近的用户并形成匿名集，匿名集的最小边界矩形作为匿名区域发布。这里存在一个很强的假设，即“所有用户均可信”。但在实际应用中并非如此:第一，网络中不存在任何可信实体。每一个用户都可能成为恶意用户，向第三方提供他人真实位置或其它敏感信息。第二，由于不存在任何可信实体，所以不是所有用户愿意共享真实位置。为寻找邻近用户而利用的“精确位置”正是用户想要保护的对象。所以现有的利用确切位置寻找匿名集的方法应用领域有限。亟待寻找一种在不提供确切位置的前提下为半可信用户寻找匿名集的方法。

由于网络中不存在任何可信实体，本文采用主从分布式结构，为半可信用户提供位置隐私保护。在基于位置服务中为半可信用户匿名的问题可分解为两个子问题:第一，在无位置信息的前提下，如何寻找空间位置邻近的用户形成匿名集;第二，匿名集中用户如何在不暴露精确位置的情况下计算空间匿名区域。为解决上述两个问题，本文提出了一种基于k*最近邻图的匿名方法，并通过“协作”的方式生成匿名区域。具体来讲，每一个用户通过无线信号强弱维护一个当地k*最近邻，并发送给第三方，如基站。第三方通过每一个注册用户的发来k*NN维护一个k*最近邻图。为保证最近邻一致性，把图划分为若干个极大团，并通过极大团扩展寻找匿名集。在找到的匿名集中，每个用户均根据自己的隐私需求向匿名区贡献一点位置，基于这种思想协作生成匿名位置。

图1 主从分布式系统结构

1 系统结构

本文采用主从分布式系统结构，包括客户端、基站和服务提供商，如图1所示。具体工作流程如下:第一，用户首先在基站注册LBS服务，然后打开无线传感设备，本地维护k*NN信息。基站根据所有注册用户发来的k*NN信息，更新、维护近邻图关系图。第二，用户向基站发送匿名请求。基站利用匿名集生成算法将所有用户分组，并为查询提出用户寻找合适的匿名组。携带组内成员列表给相应成员发送通知信号。组内成员通过自组织的方式利用匿名区域生成算法协作计算匿名位置。组内其他用户在更新k*NN之前，如果提出任何查询均以该匿名区域为准。第三，请求匿名的用户将带有匿名区域的查询发送给服务提供商。服务提供商回答该查询后，将候选结果集返回给用户。用户根据自己真实的位置挑选出确切结果。第四，当用户离开系统时，向基站提出请求，从邻近关系图中删除该结点，以及与该结点邻接的所有边。

2 基本定义

定义1(p－同谋隐私模型) 设每个移动用户u的最小隐私度需求为p。系统中任意两个或两个以上的半可信实体，通过交换各自的以及共同拥有的背景知识，推算用户u敏感信息的概率记为P(u)。对于系统中的任意用户u，如果P(u)≤p，则称用户u满足p-同谋隐私模型。本文主要关注的是敏感位置信息，故每一个半可信用户的精确位置泄露概率不能超过p。

定义2(匿名集) 用户集合CR是匿名集，当且仅当

(1)|CR|≥K，|CR|表示集合CR的大小，即集合包含的元素个数，K即用户的匿名度需求;

(2)∀u∈CR，满足p-同谋隐私模型;

(3)maxT是用户可容忍的最差服务质量，匿名集CR匿名区域大小Area(CR)≤maxT。

位置隐私保护基本任务即将服务空间中的用户分组，每一个分组中的每一个用户的隐私需求均得以满足，同时该分组组成的匿名集集合匿名代价最小。本质上，该问题是一个组合优化问题。形式化表示如下:

定义3(用户划分) V是服务空间中所有等待匿名的对象组成的集合，将V中用户按某种规则分组，则 CU={CS1，CS2，…，CSn}，其中

(1)CS1∪CS2∪…∪CSn=V;

(2)对于任意 i，j，CSi∩CSj= Ø;

(3)cost(CU)最小。

如前所述，由于用户间不可信，每一位用户均不发布精确位置，而是通过判断对等点间的信号强弱判定用户的邻近关系［4］。利用带权无向图表示用户间的邻近关系，并证明了在该图上寻找匿名集等价于在图中寻找K－簇的问题。所以定义3在邻近关系图上修正为定义4。

定义4(图划分) V是图中所有顶点组成的集合，P={P1，P2，…，Pn}，其中

(1)P1∪P2∪…∪ Pn=V，其中Pi是一个连通子图;

(2)对于任意的 i，j，Pi∩Pj= Ø;

(3)costG最小，这里图的划分代价用所有连通子图的边权值和表示。

3 匿名算法

匿名算法的基本思想是首先将用户分组，每一个组中任意两个对象都相互邻近，从而使得匿名集的总代价最小。进而，在每一个匿名组中，利用“协作”的方式生成匿名区域。

3.1 寻找匿名集

在邻近关系图上，为把用户分组，最直观的方式是寻找最近邻，即依次针对每一个用户，寻找其(K－1)NN，将此K个用户聚集在一起。图2给出了一个根据用户信号得到的邻近关系图，其中边的权重代表信号强弱(值越小代表越近)。假设K=3，首先扫描用户P1，利用寻找最近邻的方法可以获得匿名集合{P1，P2，P3}和{P4，P5，P6}，划分后的结果如图3(a)所示。很明显，此图存在另外一种更优的划分方法，如图3(b)所示。产生这种现象的原因是，对象的最近邻关系没有对称性［6］。用实验证明了对象相互最近邻一致性可以改善聚类质量，受到此点的启发，我们旨在寻找满足最近邻一致性的匿名集。

图2 邻近关系图PG

图3 邻近关系图PG的两种划分

定义5(k*相互近邻一致性) 设用户集合U，如果 ∀vi，vj∈U，并且 vi∈ lNN(vj)同时vj∈l'NN(vi)，其中lNN(vi)表示vi的lNN组成的集合。令k=max(l，l')，则称该集合用户满足k*相互最近邻一致性。

为找到满足k*相互近邻一致性的匿名集，本文采用k*最近邻图表示服务空间中用户间的邻近关系。

定义6(k* 最近邻图) k*最近邻图(k* nearest neighbor graph，k*NNG)是一个无向带权图G(V，E，ω)。其中

(1)V是活动用户组成的集合;

(2)E 是无向边组成的集合 E={(vi，vj)| ∀vi，vj∈ V，vj∈ k*NN(vi) 并且 vi∈ k*NN(vj)}，其中kNN(vi)是vi的kNN组成的集合;

(3)ω表示对象间的邻近度。值越小说明两个点的距离越近，反之说明距离较远。

现在的问题是要从k*NNG中寻找满足最近邻一致性的用户集。很明显，这些用户集正好组成了k*NNG的团。所以首先计算图k*NNG G的补图¯G，然后利用经典的WP着色算法［7］在¯G上寻找所有极大独立子集，这些极大独立子集正是图G的极大团集合。受篇幅的限制，经典的WP着色算法被省略。本文将所有的极大团集合分为两类:正团和负团。

定义7(正团和负团) CS是有极大团组成的集合。对于任意极大团C∈CS，如果|C|≥K，则成该团为正团;否则，称此团为负团。

当K值较大时，由WP着色算法生成的可能大部分是负团，不能满足隐私度K的需求。为了解决此问题，提出扩展策略。基本思想是取出负团中的每一个顶点，进行宽度优先搜索，将与该负团邻接、合并后权值和最小的团选择出来合并。重复上述过程，直至负候选的数量为零。具体算法如图4(a)所示。

3.2 寻找匿名区域

在定义1中给出了p－同谋隐私模型。在此节，简单起见，将此模型具体化为:设匿名集合为CS，u为CS中的任意用户，当CS中|CS|－1个用户相互串通时，他们根据中间结果和背景知识推测u在一维空间上的位置范围为［loc1l，loc1r］，则|loc1r－loc1l|的长度不能小于P(=p*min(width，height))，其中p是用户的最小隐私需求，width/height为系统的宽/高)。如果一维情况下的x(y)轴方向上，用户位置隐私分别得到了满足，则用户的精确位置也不存在泄露的危险。

匿名区域生成的基本思想是:作为提出查询的触发用户，首先做出牺牲，提出一个满足触发用户最小隐私度的候选匿名区域。将候选匿名区域依次传递给匿名集中的其他用户，其中每一个用户选取候选匿名区域Top/Down(Right/Left)方向中的一个，根据自身隐私需求，生成适当的随机数δ。在选取的扩展方向上，将候选匿名区域的长和宽扩展δ。

下面在具体说明如何选取扩展方向和扩展度δ之前，首先将一个用户相对于一个矩形的位置分为4种。

定义8 设矩形R和点V，计算由R和V形成的最小边界矩形MBR。如果V仅对MBR边界的x(y)值有贡献，则称V是x(y)型点;如果V对MBR边界的x和y值同时有贡献，则称V是xy型点;如果V被R覆盖，则称V是内型点。

下面根据用户点的位置类型，设计不同的扩展规则。

规则1 触发用户从［P，maxT］范围内分别取随机取两个数R1和R2，其中maxT是系统值，说明了用户可接受服务质量的最差值。分别以R1和R2作为长和宽，生成一个覆盖用户当前位置的矩形R。用户真实位置随机出现在该矩形内的任意一点。

触发用户将此候选区域R发送给匿名集中的其他用户，接收用户根据自己位置点的类型选择扩展规则。方便起见，设wid为候选区域R的宽，hgt为候选区域R的高。

规则2 如果接收用户u是x型点，设从［bn，maxT－wid］范围中按照高斯分布取随机数rn，其中

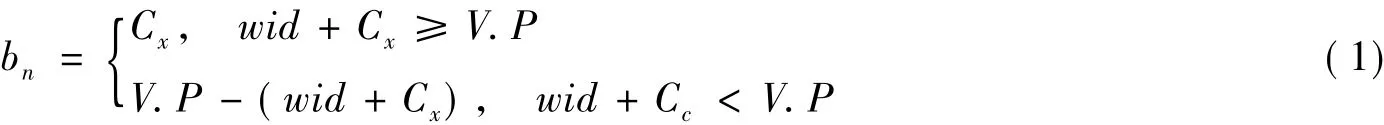
式中，Cx是用户u在x轴方向上对边界的贡献。设扩展长度为δn，则

从Top/Down方向上随机选取一个方向dir，则在用户贡献Cx的方向和选取的方向dir上扩展δn。

规则3 如果接收用户是y型点，设从［bn，maxT－hgt］范围中按照高斯分布取随机数rn，其中

设扩展长度为δn，则

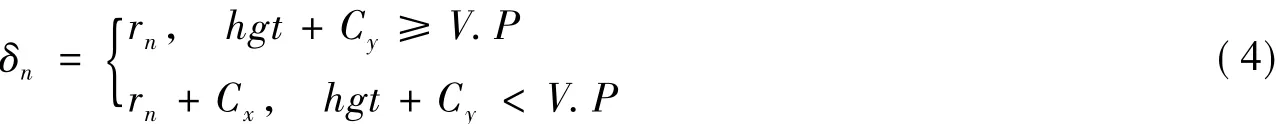
从Right/Left方向上随机选取一个方向dir，则在用户贡献Cy的方向和选取的方向dir上扩展δn。

结合规则2和规则3，可得xy型点的扩展规则。

规则4 设利用规则2计算x方向的扩展度δx，利用规则3计算y方向的扩展度δy，候选匿名区域的扩展度 δn=max(δx，δy)。从 Cx和 Cy贡献的方向上均扩展 δn。

规则5 如果接收用户是内型点，并且候选匿名区域R的宽或高小于用户最小隐私需求V.P，则按从［V.P－min(wid，hgt)，maxT－min(wid，hgt)］范围内按照高斯分布取随机数δn。并随机的从Top/Down和Left/Right方向上任取一个方向dir1和dir2。在dir1和dir2方向上同时扩展δn。

由规则2～规则5，可以发现虽然是根据不同用户类型，选择不同的扩展随机数和方向，但是从攻击者的角度，用户均是从候选匿名区域x和y方向上分别扩展了δn。不同位置的用户类型在外界看来无异，维护了用户的位置隐私。图4(b)给出了匿名区域生成算法。

4 实验

4.1 实验设置

图4 匿名算法

为不提供真实位置用户寻找匿名集，直观上容易想到的方法是:每一位用户均发布满足个人隐私需求的模糊位置，通过寻找基于模糊位置的KNN形成匿名集，简称该算法KNNCloak。本节用实验的方式评估KNNCloak和本文提出算法(简称NNClique)在不同系统设置下效率和质量。使用著名的Thomas Brinkhoff移动对象生产器［8］生成模拟数据。由于NNClique算法假设用户通过信号强弱判断位置邻近，所以首先计算出每一个用户的20NN，并形成一个最近邻图。为适应KNNCloak，在进行匿名前首先将所有用户的位置按照用户最低隐私度需求p生成一个矩形代表模糊位置。所有用C++实现，运行于1.83 GHz处理器、2 GB内存的台式机上。模拟之初，生成10 000个移动对象，实验默认隐私度K为10，最差服务质量maxT为1 000个系统单元，最低隐私需求p是从［0.08%，0.2%］的系统宽度中取的随机数，在为对象寻找匿名区域扩展时扩展宽度的随机数满足数学期望为2p、标准方差为1的高斯分布。

4.2 性能评测

图5显示了匿名成功率随着隐私度和最差服务质量变化的变化趋势。隐私度K增加说明在一个匿名集中包含的用户的增多。但是，隐私度的变化对KNNCloak无影响，其匿名成功率基本保持在98%～99%。而NNClique的成功率随着K的增加而直线降低，这与用户临近用户数有关。在图5(b)中仅评测了NNClique在不同maxT下成功率的变化趋势。最差服务质量降低，即用户对服务质量的要求提升了。所以从图5中可以看出，匿名成功率逐渐降低，但是当maxT降低到100时，匿名成功率依然在96%以上。

平均匿名代价指的是对于每一个匿名集合来说，匿名区域的平均面积。图6中的TightMBR是根据匿名集用户的真实位置计算的最小边界矩形MBR的面积。把它包括在这里是为了比较显示，由于用户半可信牺牲的匿名代价。如图6(a)所示，随着隐私度的增加，NNClique和KNNCloak的匿名代价均上升，因为匿名集中覆盖了更多的用户。但是从图6(a)中依然可以看出，NNClique为了保护半可信用户隐私，与精确位置隐私保护相比牺牲了多于2倍的服务质量。如图6(b)所示，随着最差服务质量的降低，平均匿名代价也急剧降低。当最差服务质量降低到600时，牺牲的服务质量节省了一倍。

NNClique的匿名时间包括两部分:寻找匿名集的时间(图7中的黑色柱)和计算匿名区域的时间(图7中的白色柱)。无论是随着隐私度的升高还是随着最差服务质量的降低，寻找匿名集和匿名区域的时间均逐渐增加，但是后者增长缓慢。而在匿名区域生成部分，随着匿名集中保护用户数的增多，候选匿名区域需要征询更多人的意见方可决定，故寻找匿名区域的时间也增加的，但是增加幅度不大。二者结合即为本工作中查询的匿名时间，可以看出匿名时间中寻找合适用户占去将近2/3的时间。最差服务质量变化趋势与图7(a)类似，其原理也相同，故这里不赘述。

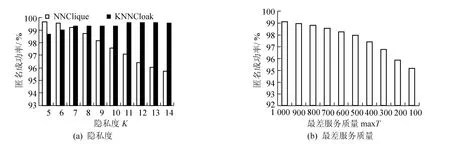
图5 匿名成功率

图6 平均匿名代价

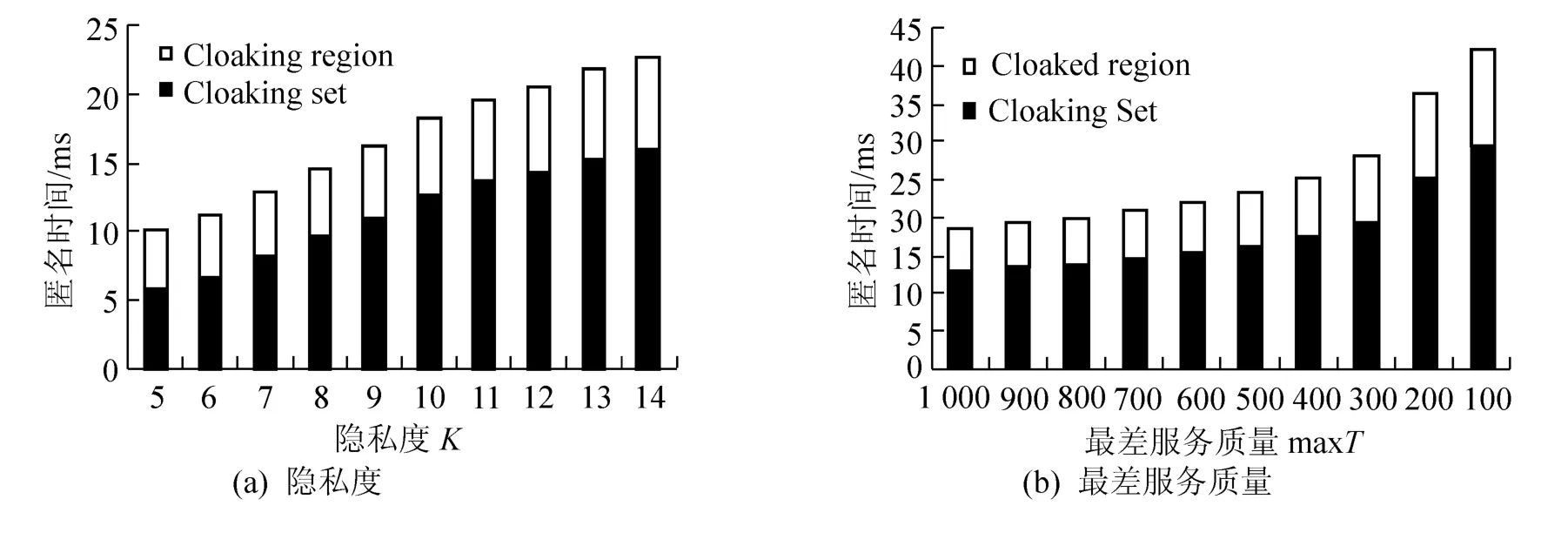
图7 平均匿名时间

5 结论

提出了一种在主从分布式环境下，为半可信用户提供位置隐私保护的方法。观察到现存的大部分位置匿名方法均假设用户可信，但是这在网络中并不现实的。为解决此问题，本工作根据用户信号强弱判断位置邻近性，提出了一种在K*NNG上的匿名算法，并通过“协作”的方式完成的匿名区域生成过程。在不同的系统设置下对算法进行实验，结果表明基于半可信用户的方法虽然牺牲了大致2倍的服务质量，但是与在模糊位置上直接寻找KNN的匿名算法相比，在效率和服务质量上取得了较好的平衡。

［1］SWEENEY L.K－anonymity:a model for protecting privacy［J］.International Journal on Uncertainty.Fuzziness and Knowledgebased Systems，2002，10:557－570.

［2］PAN X，MENG X，XU J.Distortion－based anonymity for continuous query in location－based mobile services［C］//In Proc of ACM SIGSPATIAL GIS.Washington，2009:256－265.

［3］PAN X，XU J，MENG X.Protecting location privacy against location－dependent attacks in mobile services［J］.IEEE Trans.Knowl.Data Eng，2012，24(8):1506－1519.

［4］HU H ，XU J.Non－exposure location anonymity［C］//Proceedings of the 25th International Conference on Data Engineering(ICDE).Washington:IEEE Computer Society，2009:1120－1131.

［5］MOKBEL M F，CHOW C，AREF W G.The New Casper:query processing for location services without compromising privacy［C］//Proceedings of the 32nd international conference on Very large data bases(VLDB).Seoul:VLDB Endowment，2006:763－774.

［6］DING C H，HE X.K－nearest－neighbor consistency in data clustering:incorporating local information into global optimization［C］//Proceedings of the ACM symposium on Applied computing(SAC).New York:ACM Press，2004:584－589.

［7］WELSH D J A，POWELL M B.An upper bound for the chromatic number of a graph and its application to timetabling problems［J］.The Computer Journal，1967，10:85－86.

［8］BRINKHOFF T.Thomas Brinkhoff Network － based Generator of Moving Objects［R/OL］.Oldenburg:Jade University，2013.http://www.fhoow.de/institute/iapg/personen/brinkhoff.