销孔间隙与孔壁承压容许应力取值研究

李铁纯， 王海林

(石家庄铁道大学国防交通研究所，河北石家庄 050043)

0 引言

销连接是较为常见的一种传力结构形式，它结构简单、传力明确、使用方便，在机械工程和工程建设中应用很广。在实际工程中，为了安装方便，销孔和销轴之间会预留一定的间隙。国内规范对销孔间隙并无具体规定，只是要求销孔间隙尽可能小［1］。接触受力的材料处于三向受力状态，其应力分布复杂，尤其是当销孔间隙增大时，耳板孔壁压应力急剧增大，威胁到了销结构的安全使用。设计人员凭经验对销接结构进行设计，销孔间隙取多少既能满足安装需要又能满足安全要求，是一个亟待解决的问题。

有限元方法是解决各类复杂工程实际问题中设计、研究及优化的有力工具，它已成为当今结构分析的最有效的方法和手段。目前常采用刚域法、BE3法、接触法建立销接结构接触的有限元模型［2］。接触法通过在销轴孔与销轴之间建立接触单元实现销接结构接触模型的建立，这种方法能较真实的模拟销结构的接触情况。现基于有限元分析软件ANSYS采用接触法建立销结构的有限元模型。

1 销结构的构造和有限元模型

1.1 销结构尺寸的确定

1.1.1 计算销轴的直径

销轴的破坏形式有销轴剪切破坏、销轴弯曲破坏、销轴承压破坏。目前国内对销轴的设计尚无统一的设计标准，一般按照JTJ 025—86规范［3］对销轴进行设计，此处假设销轴直径取36 mm。

1.1.2 确定耳板的厚度和开孔的位置

式中，［σp］为孔壁承压容许应力;σp为孔壁承压计算应力;F为单个耳板承受轴力;d为销孔直径;t为耳板厚度。

单个耳板承受轴力F取108 kN，Q345钢［σp］取300 MPa。计算可得厚度t取值为10 mm。

由规定一:垂直受力方向销孔直径处的净截面面积应比杆件计算所需的面积大40%，可得

式中，A为耳板的计算面积;a为孔边距;t为耳板厚度。

A=F/［σ］ =108 000/200=540 mm2，t取10mm。计算可得孔边距 a ＞37.8 mm。

由规定二:由销孔边至杆端的截面积应不小于杆件的计算截面积，可得

式中，b为孔端距;t为耳板厚度。

t取10mm，A取540 mm2。计算可得孔端距b＞54 mm。取耳板销孔直径为36 mm，如图1所示。

1.2 销结构有限元模型

1.2.1 销结构有限元模型参数设置

建立销结构有限元模型时，销轴和耳板均采用Solid95单元，3D接触面用CONTA174模拟，3D目标面用TARGE170模拟。销轴的两侧施加固定;在耳板的一侧施加拉力，以均布荷载的形式施加在节点上;为了防止耳板绕销轴转动，还需在耳板一侧施加y、z方向的约束。

图1 耳板尺寸设计图(单位:mm)

图2 耳板有限元模型图

模型采用双线性随动强化BKIN，弹性模量EX取值为206 GPa，泊松比取值为0.3。耳板采用Q345钢，屈服强度为345 MPa;销轴采用强度较高的40Cr，屈服强度为760 MPa。由于需要大量的计算，为了节约程序运行时间，模型采用单个耳板，如图2所示。销结构的有限元模型总共有3 064个单元，17 097个节点。接触问题是一种高度非线性行为，其收敛的过程需要经过反复的调试，选取合适的参数。本模型中CONTA174单元KEYOPT(5)=3，用自动CNOF闭合间隙、降低侵入。实常数FKN=0.01、FTOLN=0.1，这两个实常数的选取需要根据计算的收敛情况确定。

1.2.2 销结构模型参数设置验证

大量的计算实践表明，有限元软件ANSYS所提供的接触分析方法本身是可靠的，但注意到成功地分析结果不仅仅取决于计算方法是否可靠，在很大程度上还取决于分析模型与工程问题的近似程度。具体来说，有限元模型中接触刚度、侵入距离、接触方式类型和接触区域的网格密度等物理性质参数的设定对分析结构会产生较大的影响［4］。为了验证本文销轴结构有限元模型的可靠性，现将本模型的数值分析结果与理论规律进行对比。

在进行弹塑性分析之前，先进行弹性分析，将所得结果与采用赫兹理论计算出的结果进行比较，以此验证相关参数设置的可靠性。销轴直径为36 mm，不同销孔间隙时，耳板最大弹性接触压应力如表1。

表1 不同销孔间隙结果对比

由表1可以看出:随着销孔间隙的增大，耳板最大接触压应力的值也在增大。理论值和本文有限元模拟值基本一致。

2 销轴直径D=36 mm时耳板孔壁承压容许应力分析

在耳板侧端施加F=108 kN的力时，耳板孔壁承压应力为:σp=F/dt=108 000/(36×10)=300 MPa，正好等于耳板容许压应力。销轴和耳板直径均为36 mm时，分析耳板塑性变形，如图3、图4所示。

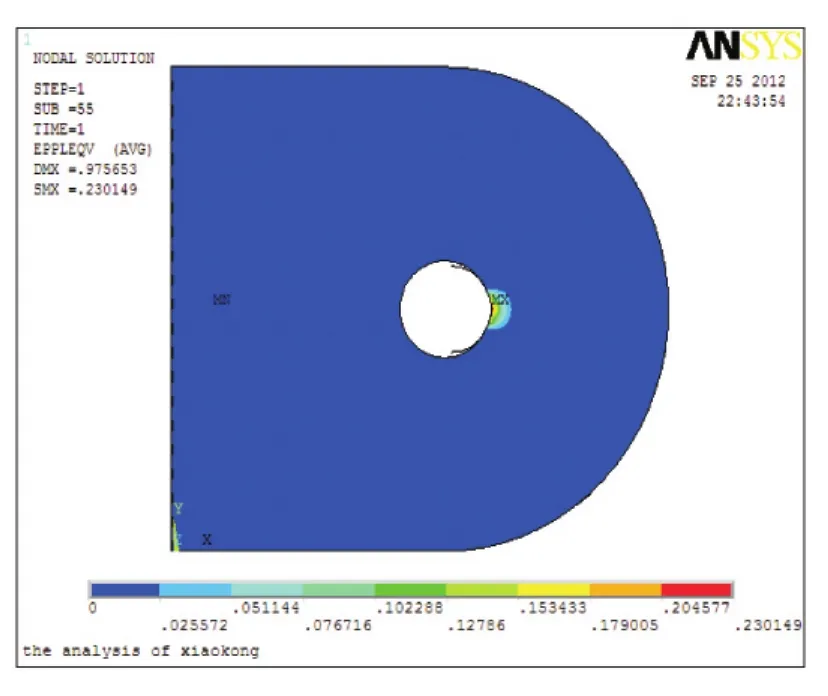
图3 耳板塑性变形图

图4 耳板局部塑性变形放大图

由图3和图4可以看出:耳板塑性区域仅发生在销轴与耳板接触区域即C-C截面内侧，该区域面积很小，且塑性应变值由里向外呈层状递减。耳板受载后接触部位产生局部塑性变形，这是由于接触区域应力集中现象存在。接触处局部塑性应变很大，接触面稍远处塑性应变急剧下降。耳板B-B截面内侧受拉部位未发生塑性变形，说明该区域拉应力小于屈服强度。

耳板厚度为10 mm，本文选用耳板底部和耳板中部塑性区面积的均值作为衡量不同销孔间隙下耳板塑性变形能力的标准。销轴直径d=36 mm时，塑性区面积均值为S=(S1+S2)/2，其中，S1为图5中沿厚度方向t=0时耳板塑性区面积，S2为图6中沿厚度方向t=5 mm耳板塑性区面积，计算得S=57.6 mm2。固定销轴直径不变，依次改变销孔直径大小，然后进行大量计算，使得耳板达到同样的塑性区面积，此时的耳板孔壁名义承压容许应力为［σc］=F/dt。销轴直径为36 mm时，耳板孔壁名义承压容许应力结果见表2。

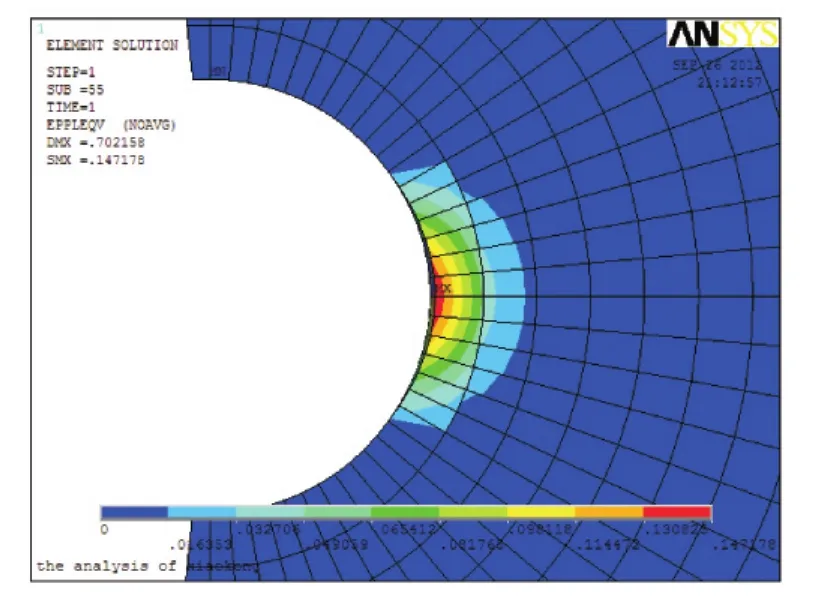
图5 耳板顶部塑性区面积

图6 耳板中部塑性区面积

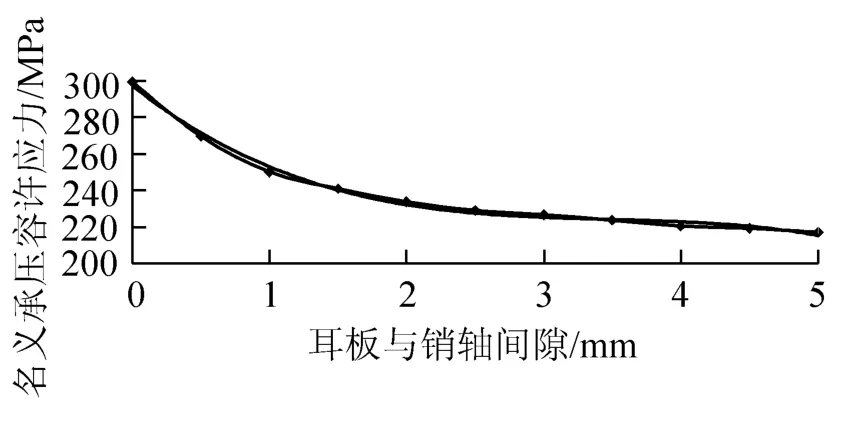
图7 耳板孔壁名义承压容许应力拟合曲线

由表2可以看出:随着耳板销孔直径增大，销孔与销轴之间的间隙随之增大，耳板在相同的塑性区面积时，耳板拉力降低。耳板孔壁名义承压容许应力随着间隙的增大减小。

三次曲线能较好地拟合曲线规律，具体拟合情况见图7。

由图7可以看出:随着耳板与销轴间隙的增大，耳板孔壁名义承压容许应力呈下降趋势，且下降速度随着间隙增大而变缓。当二者之间的间隙为0～1 mm时，耳板孔壁名义承压容许应力下降的较快，二者之间的间隙为3 mm至5 mm时，耳板孔壁名义承压容许应力下降较慢。

由图7可见，拟合曲线具有较好精度，拟合公式为

式中，x为耳板与销轴间隙;y36为耳板孔壁名义承压容许应力。

3 结论

参照有关技术规范的规定，依托有限元软件ANSYS建立了不同销孔间隙的有限元模型，进行了详细的研究，结论如下:

(1)针对材质的弹性阶段，将有限元结果与理论值进行了对比，两者数值吻合良好，说明有限元分析方法的可靠性［5］。

(2)采用扩大耳板直径的办法获得销孔间隙，通过大量计算，研究了不同间隙下耳板孔壁名义承压容许应力的变化情况，得出如下规律:耳板孔壁名义承压容许应力随销孔间隙的增大而减小，当销孔间隙为0～2 mm时，耳板孔壁名义承压容许应力下降较快。

(3)对耳板孔壁名义承压容许应力随销孔间隙的变化规律进行拟合，得到的拟合公式具有较好精度。

本文对直径为36 mm的销轴进行了研究分析，其他直径的销轴结构还有待进一步研究分析;采用计算耳板底部、中部塑性区面积算术平均值的办法求出塑形区面积，以此近似求解不同销孔间隙情况下耳板塑性变形情况。若想精确模拟实际情况，可以用耳板发生塑性变形的体积为“桥梁”做进一步研究。

［1］应天益.国内、外桥梁销接节点设计方法［J］.世界桥梁，2011(2):22-25.

［2］吴雪梅，李瑰贤，郭峰，等.销轴连接的几种有限元模型比较［J］.机械工程师，2004(1):67-68.

［3］交通部公路规划设计院.JTG 025—86公路桥涵钢结构及木结构设计规范［S］.北京:人民交通出版社，1988.

［4］张军，张恒，张洛明，等.基于接触的销钉孔塑性变形分析［J］.郑州大学学报:工学版，2010，31(4):81-84.

［5］颜东煌，刘雪锋，田仲初，等.销轴连接结构的接触应力分析［J］.工程力学，2008，25(1):229-234.