基于点光源的迈克耳孙干涉实验条纹的机理分析

李贤芳 李建青 马争争 余灵凤

（武汉理工大学物理系，湖北 武汉 430070）

在一般大学物理的教材［1，2］中，只介绍了以平行平面薄膜的等倾或等厚的分振幅型干涉，类似地，在大学物理实验教材［3］中，也只是介绍了通过等倾干涉所产生的圆条纹现象的观察及相应的物理量的测量.然而，迈克耳孙干涉仪可以调制出椭圆和双曲线干涉条纹，但其条纹形成的理论推导很少涉及.本文将根据点光源双光束干涉理论对迈克耳孙干涉仪各种不同形状条纹产生的机理进行理论分析和比较.

1 点光源双波场的双叶双曲面的形成［4］

如图1所示，令P（x，y，z）为干涉场中一考察点，S1，S2为两初相位相同，相距为d，强度相等的两相干点光源.则在真空中有光程差：

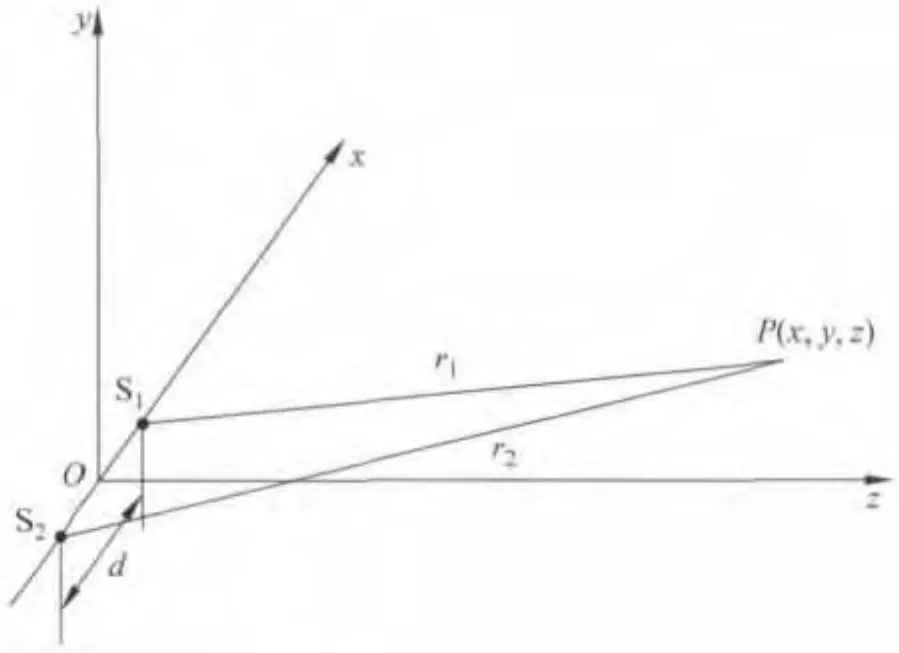
图1 双光束干涉的几何关系示意图

整理后得方程

由于Δ≤d，由解析几何知，这是以S1，S2为焦点，以x轴为旋转轴的旋转双叶双曲面，如图2所示.d为定量，则每一Δ值对应两个对称的相应曲面，双叶双曲面的几何意义是该曲面上任意一点至两焦点的距离差为一常数点的轨迹，而对于P到S1，S2的距离差为常数的物理意义正是“光程差恒定”之意，故该组双叶双曲面正是等光程差曲面，显然，x＝0时，对应光程差Δ＝0.

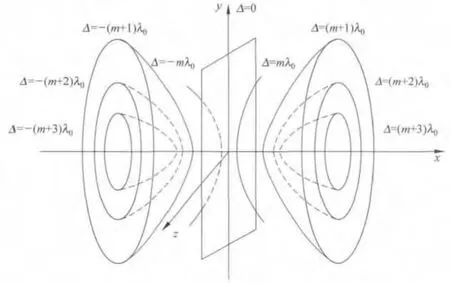
图2 两点光源的等光程差曲面

2 接收屏上干涉条纹的几何形状及形成条件

因为S1，S2两光源的光强相等，则干涉条纹就是一族等光程差线，若用接收屏（如毛玻璃）接收，实质上就是接收屏与等光程差曲面相交的截线，下面讨论几种典型的干涉条纹形状.

2.1 接收屏上双曲线条纹的形成条件

显然，当接收屏为z＝D平面时，干涉条纹为z＝D平面与等光程曲面的交线，故有

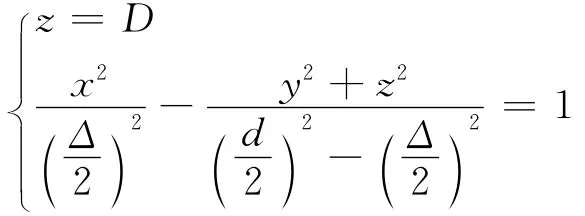
解此方程组，得到

这是一组双曲线方程，所以z＝D平面上的干涉条纹呈双曲线规律分布.由于旋转双曲面是对x轴旋转对称的，因此在任一与x轴（两点光源连线）平行的平面上，其干涉条纹皆为双曲线形状.若接收屏离O点足够远，即且P点在z轴附近（近轴条件），此时可将z＝D代入光程差公式（1）并用二项式定理展开，忽略高次项有

所以有

条纹间距

这是一些平行于y轴的直线，故在z＝D屏面上在满足近轴条件的情形下，得到的干涉条纹是一族平行于y轴的等距分布的直线干涉条纹（此即近轴条件下，双光束干涉得到平行等距干涉条纹的由来）.

2.2 接收屏上圆形条纹的形成条件

同理，在接收屏为x＝D平面上（与S1，S2两光源连线垂直平面）

整理得

显然，这是一组以x＝D平面与x轴交点为圆心的一族同心圆，故此时x＝D平面截得的条纹形状为一族同心圆环形条纹，k为圆环半径.当x＝0时（yOz平面），该平面上任意点的光程差皆为零，此时光强最大，故该接收屏被均匀照明.

2.3 接收屏上椭圆条纹形成的条件

当接收屏不在上述位置时.设接收屏的法线在xOy屏面上，法线与接收屏相交于x0，y0，法线与x轴成θ角，在接收屏上取（m，z′），如图3，x，y，z坐标与接收屏上得m，z′坐标的转换关系为

将式（6）代入式（2）即得此接收屏与等光程差曲面截线在m，z坐标系中的方程.代入得

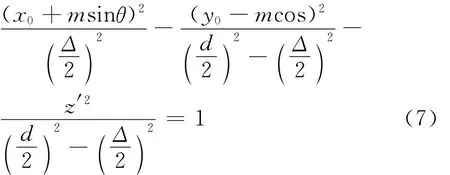
这是一个m，z′坐标上的二次曲线的方程，根据解析几何知识，当z′2与m2的系数同号时，则曲线为一椭圆，将该式展开整理可得m2的系数为，现z′2项的系数为负值（d≥Δ），故椭圆出现的条件为，即

如不满足此条件，则接收屏上得到的是双曲线干涉条纹.综合以上情况，点光源双光束干涉条纹的形状随屏幕位置变化的规律用图像表示为（图4）.

3 迈克耳孙干涉实验条纹的分析［5，6］

3.1 迈克耳孙干涉实验原理

图5是迈克耳孙干涉仪的等效光路图，设M′2与之间的距离为，氦氖激光器中发出的平行光经透镜（扩束镜）L汇聚得点光源S，S经AB膜反射成镜像于S1，S1再经 M1和 M′2成镜像于S′1，S′2；由几何光学知识可知S′2与S′1之间的距离为d.因为S′1，S′2分别来自于同一光源S，故S′1与S′2是相干的.此时，迈克耳孙干涉仪的干涉条纹可以等效看成是由 S′1，S′2产生的干涉，这样，用激光照明的干涉仪，就等效为两个单色点光源S′1与S′2的干涉.

图4 条纹形状随接收屏位置的变化

图5 迈克耳孙干涉仪等效光路图

图6 等倾干涉光程差分析图

3.2 迈克耳孙干涉仪的各种条纹的形成条件

由前面分析可知，对于两点光源产生的双光束干涉，接收屏上干涉条纹的形状将随着接收屏与产生干涉的两相干点光源连线的相对位置的改变而改变.对于迈克耳孙干涉仪，接收屏的位置是固定在一个方位上，且S′1，S′2的连线位置是由 M1与M′2的相对位置决定，此时要获得不同形状干涉条纹，只能改变M1与M′2的相对位置.

1）圆条纹的形成条件

当激光束垂直于M1，且M′2与M1平行，此时接收屏垂直于S′1与S′2的连线，接收屏接收到的为一束同心圆环型条纹，即等倾干涉，其光程差分析如图6.

将此式用二项式定理展开得

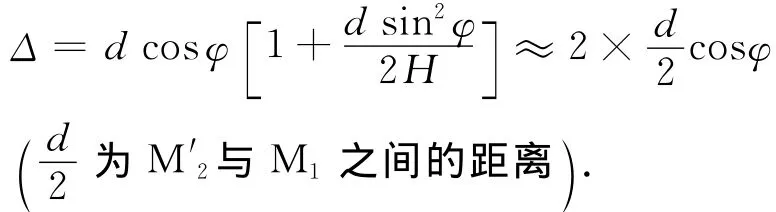
该光程差公式表明，在 M′2与 M1平行的条件下，即d一定，光程差只与φ有关，此为等倾干涉.

2）直条纹的形成条件

当M1与M2到分光板G1的距离近乎相等，即M′2与M1相交（膜厚趋于零），且两者有微小夹角时，M1与 M′2将形成两个对顶的空气劈尖，如图7所示，此时S′1与S′2的连线基本上与接收屏平行，则接收到的条纹中间是直线，两边呈对称分布的双曲线.因为迈克耳孙干涉仪的接收屏很小，基本满足近轴条件，所以实际接收到的是近乎直线的条纹.这种情况通常说成是等厚干涉.

3）椭圆或双曲线条纹的形成条件

当M′2与M1不平行且不相交，（膜厚较大，远大于λ）如图8，因为M′2与M1之间有较厚的空气层，此时S′1与S′2的连线与接收屏既不平行也不垂直，接收屏得到的是如图8所示的椭圆或双曲线条纹.很明显此种干涉情况既非等倾也非等厚.对于实际情况，因为干涉仪中的接收屏视场很小，所以观察到的只是椭圆或双曲线的一部分，有时候难得判断是椭圆还是双曲线，但是根据干涉原理，可以判断曲线条纹的弯曲方向.原因是：如果M1与M′2的距离较大（即d较大），则φ的微小变化将引起Δ的较大变化，故条纹与等厚线的偏离程度增大，这时条纹将发生弯曲，弯曲的方向是凸向楔棱（M1与M′2延伸面的相交线）.如图9所示.

图7 直线与双曲线条纹

图8 迈克耳孙干涉仪既非等倾也非等厚的干涉

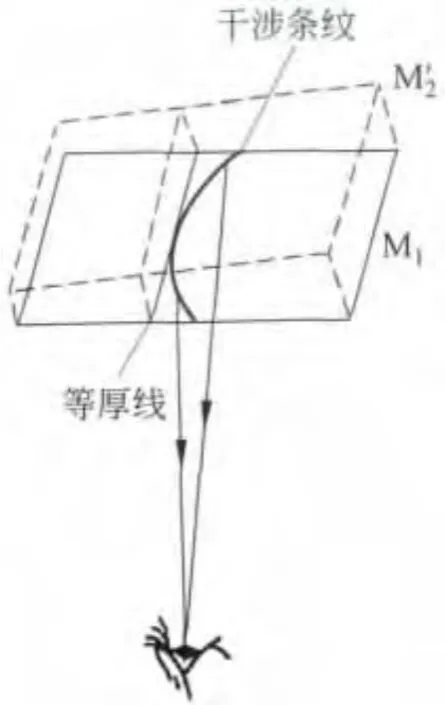
图9 干涉条纹偏离等厚线

曲线干涉条纹凸向楔棱的原因定性分析是：干涉条纹是等光程差线，当入射光并非平行光时，对于倾角较大的入射光束，它所对应的光程差若与倾角较小的入射光束对应的光程差相等，应以平板厚度的增大来补偿，这一点从光程差公式Δ＝2×cosφ可以看出.因靠近楔形板边缘的点对应的入射角较大，因此，干涉条纹越靠近边缘越偏离到厚度更大的地方，所以在厚板的情况下光束入射角的变化将引起光程差较大的变化，这样条纹的弯曲将显露出来.

4 结语

迈克耳孙干涉图样较多，通过以上的分析讨论，理解每一种图样产生的原因，掌握等倾干涉与等厚干涉的条件，对学生掌握迈克耳孙干涉仪的应用及快速准确地调试，减少测量误差将有很大的帮助.

［1］ 赵凯华，钟锡华.光学（上册）［M］.北京：北京大学出版社，1985：56－80.

［2］ 马文蔚.物理学教程（下册）［M］.4版.北京：高等教育出版社，2006：69－86.

［3］ 张士欣.基础物理实验［M］.北京：北京科学出版社，1997：26－50.

［4］ 汪仕元，朱俊，等.迈克耳孙干涉光程差分析模型探讨［J］.物理实验，2013，33（3）：31－34.

［5］ 梁铨廷.物理光学［M］.北京：机械工业出版社，1980：36－87.

［6］ 崔益和.迈克耳孙干涉仪干涉机理的解析法与图解法［J］.长春大学学报，2001，11（4）：26－29.

［7］ 岑敏锐.迈克耳孙干涉仪实验中干涉条纹方程的推导和模拟［J］.物理与工程，2010，20（5）：32－33.

［8］ 张汉伟，董天奇，等.基于两点光源的迈克耳孙实验分析［J］.物理与工程，2009，19（6）：27－30.