匀质三角形板和边框的转动惯量

邱为钢

（湖州师范学院理学院，浙江 湖州 313000）

常见刚体（质量均匀分布），如杆和三角形板，对于质心轴的转动惯量，由杆和三角形的几何量来表示［1，2］.文献［3，4］给出了匀质三角形边框相对质心轴转动惯量的几何量表示，他们的推导过程中，使用了不少平面几何知识.平面几何也可以用代数的方法来研究，这就是解析几何的处理思路.应用这种思路，笔者给出了文献［3，4］结论的代数推导方法，整个推导过程中可以不画图，实用方便.

考虑一个质量均匀分布的杆，线密度λ，长度为L，质量为m＝λL.垂直于杆所在平面的转轴通过原点O，杆两个端点的坐标分别为 （x1，y1）和 （x2，y2），如图1所示.

质心C的坐标为

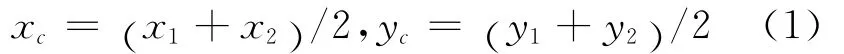
匀质杆相对质心轴的转动惯量是

由平行轴定理，匀质杆相对转轴的转动惯量为

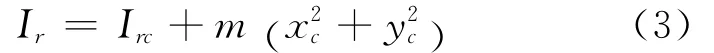
把式（1）和（2）代入式（3），计算得到匀质杆相对任意转轴的转动惯量为

图1 杆的坐标示意图

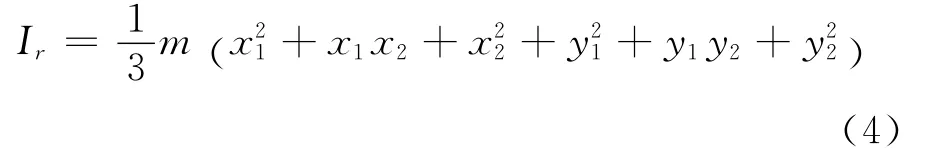
应用匀质杆转动惯量的坐标表示式（4），可以计算出匀质三角形边框相对质心轴的转动惯量.设垂直于三角形边框所在平面的转轴通过原点O，匀质三角形边框三个顶点坐标分别为（x1，y1），（x2，y2），（x3，y3），如图2所示.

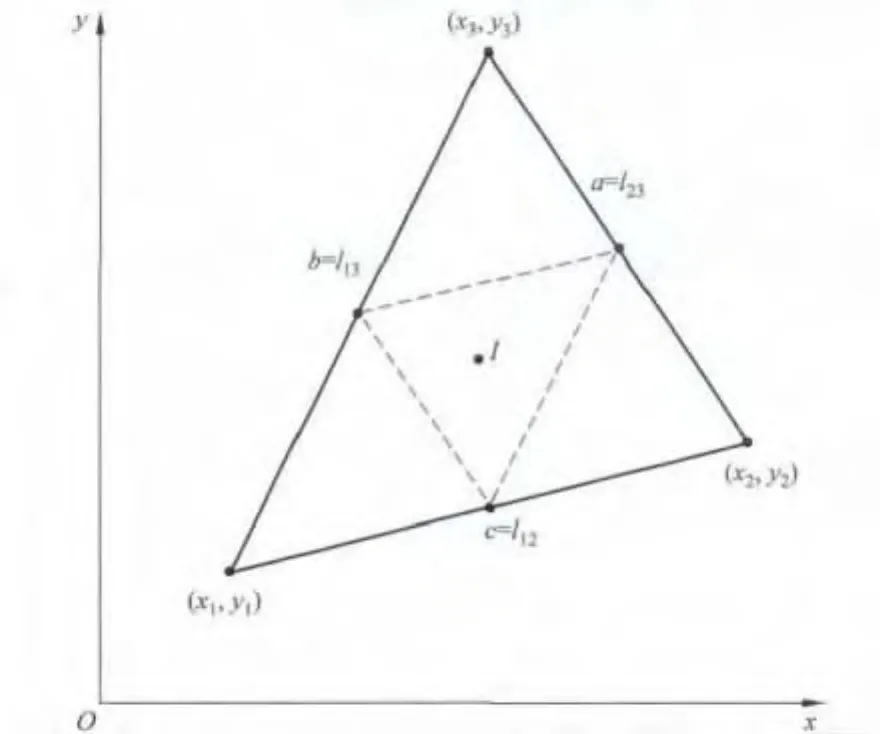
图2 三角形边框坐标与边长示意图

三角形三个边长的平方为

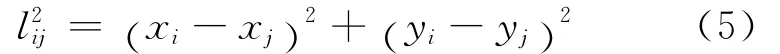
设边框（杆）的质量线密度是λ，由式（4）以及转动惯量的叠加性，得到匀质三角形边框相对转轴的转动惯量为

按定义，匀质三角形边框的质心坐标为

由解析几何知识可知［5］，匀质三角形边框的质心坐标式（7）就是中点三角形的内心坐标I.反用转动惯量的平行轴定理，得到匀质三角形边框相对质心轴的转动惯量为

式（8）的具体运算可以借助数学软件（例如Mathematica）来完成，计算发现式（8）可以写成以下表达式

利用Mathematica多项式展开和取系数功能，得到式（9）中的待定系数为

由式（9）、（10）和（11），得到匀质三角形边框相对质心的转动惯量为

作代换

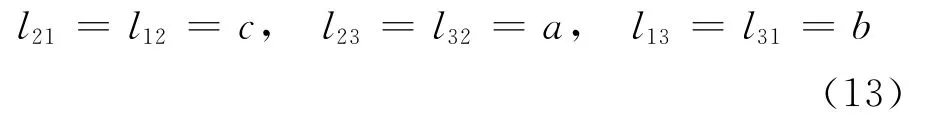
式（12）化简得到与文献［3，4］相同的结论：

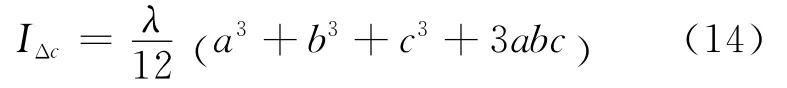
接下来求匀质三角形板相对垂直板所在平面任意转轴的转动惯量，设转轴通过原点O，m为三角形板的质量，三角形三个顶点坐标分别为（x1，y1），（x2，y2），（x3，y3）（可参考图2）.由文献［1，2］可知，匀质三角形板相对质心轴的转动惯量为

其中三角形三个边长 （a，b，c）由式（5）和式（13）确定.三角形板的质心坐标为

由平行轴定理，计算得到匀质三角形板相对转轴的转动惯量的坐标表示为

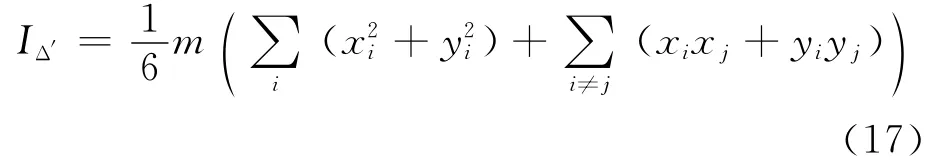
匀质杆和三角形板相对任意转轴转动惯量的坐标表示式（4）和（17），就是本文的主要结论.对于可以三角形剖分的平面物体，一旦知道了所有顶点的坐标，就可以方便利用式（17）来编程计算物体的转动惯量（面积也容易用坐标表示出来）.相比较，如用匀质三角形板转动惯量的几何表示式（15），需要知道每个三角形重心到转轴的距离，知道每个三角形的边长，计算三角形的面积（算三角形的质量），平行轴定理要反复使用，反而不如式（17）的坐标表示直接方便.

［1］ 江少林，华保盈.刚体绕任意轴转动惯量的简便计算［J］.工科物理（现刊名《物理与工程》），1998，8（3）：31－32.

［2］ 刘风智.任意三角形平板刚体的转动惯量与惯量主轴［J］.大学物理，2007，26（3）：16－17.

［3］ 周国全，徐斌富.匀质边框三角形刚体绕质心轴的转动惯量公式［J］.大学物理，2012，31（12）：8－9.

［4］ 李力.简捷推导匀质三角形边框刚体绕质心轴的转动惯量［J］.大学物理，2013，35（05）：10，43.

［5］ Incenter［EB／OL］.［2013－07－01］http：／／mathworld.wolfram.com／Incenter.html