理想气体热力学过程吸放热情况的图像判断法

郑明阳 王天为 张国锋

（1北京航空航天大学电子信息工程学院，北京 100191；2北京航空航天大学物理科学与核能工程学院，北京 100191）

在本科生热学课程中，讲完热力学第一定律后，按教学要求，需要学生掌握热力学过程的吸热或放热情况，只有会判断一个热力学过程的吸放热情况，才能准确地计算循环过程中的效率、制冷系数等等.如何非常简便地判断一个热力学过程的吸放热情况是至关重要的.

压强－体积（p－V）图上的任意一条曲线，都代表一个准静态过程；反之，任意一个准静态过程，也都可以用p－V图上的一条曲线表示.因此，可借助p－V图来研究任何准静态过程的吸放热情况.热力学中的4种最基本过程（等温、等压、等体、绝热）都可以概括为一个多方过程：pVn＝常数，n为多方指数.n＝0时为等压过程，n＝1时为等温过程，n＝γ（γ绝热比）时为绝热过程，n＝∞时为等体过程.对于一般的热力学准静态过程，虽然不能够用一个多方过程来替代，但对于该过程曲线上的任意一个无限小的微元过程，都可以看作一个多方过程的一小部分.因此对准静态过程任一微元过程吸放热的研究，可以通过研究用以拟合该微元过程的多方过程吸放热来判断，即研究该多方过程热容的正负.

热力学过程整体吸放热的情况，可以由该过程的各个微元过程相加得到.但事实上，对于整体过程吸放热的研究，并不需要像研究微观过程那样仔细，而是可以在p－V图上借助等温线和绝热线比较曲线所围面积的大小得到.

本文第一部分将讨论理想气体热力学准静态过程任意微小过程吸放热的判断，第二部分介绍判断理想气体热力学过程整体吸放热的作图方法.

1 理想气体热力学曲线上任意微元过程吸放热的研究

1.1 多方过程的摩尔热容

以下研究理想气体系统.由热力学第一定律可以得到，对于任意一个微小的热力学过程，其热量变化为

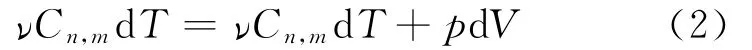
在两边分别除以νdT，并利用V＝νVm关系，则有

对于多方过程，有TVn－1＝常量，两边求全微分得

再在两边除以dT，得

由该式可得Cn，m随n值变化情况如图1所示.

图1 多方热容在p－V图上的曲线

1.2 不同n值时无限小微元过程吸放热的讨论

根据多方过程n的不同取值，对无限小微元过程吸放热情况分以下5种情况讨论：

（1）当n＞γ时，Cn，m＞0，如图2所示，虚线为绝热线，AB在绝热线下方，AC在绝热线上方.当该过程沿着A→B方向时，dT＜0，＝νCn，mdT＜0，为放热过程；当该过程沿着A→C方向时，dT＞0，＝νCn，mdT＞0，为吸热过程.

图2 n＞γ时的判断方法

（2）当n＝γ时，Cn，m＝0，为绝热过程.

（3）当1＜n＜γ时，Cn，m＜0.如图3所示，虚线为绝热线，AB在绝热线上方，AC在绝热线下方，曲线CAB夹在等温线与绝热线之间.该过程沿着A→B 方向时，dT＜0，＝νCn，mdT＞0，为吸热过程；当该过程沿着A→C方向时，dT＞0，＝νCn，mdT＜0，为放热过程.

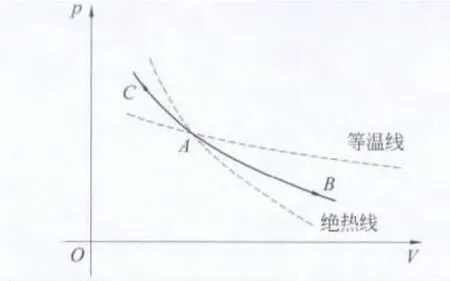
图3 1＜n＜γ时的判断方法

（4）当n＝1时，该过程为等温过程，如图4.内能变化dU＝0，虚线为绝热线，AB在绝热线上方，AC在绝热线下方，＝dU＋＝.A→B过程系统对外做正功，＞0；A→C过程外界对系统做正功＜0.

图4 n＝1时的判断方法

（5）当n＜1时，Cn，m＞0.如图5所示，虚线为绝热线，AB在绝热线、等温线上方.AC在绝热线、等温线下方.当该过程沿着A→B方向时，dT＞0，＝νCn，mdT＞0，为吸热过程；当该过程沿着A→C方向时，dT＜0＝νCn，mdT＜0，为放热过程.

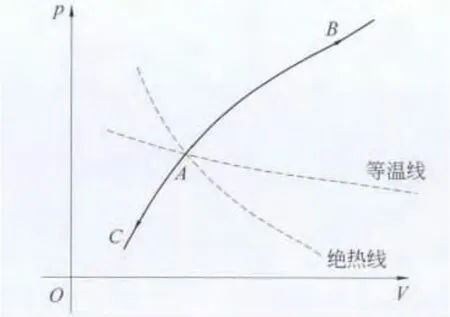
图5 n＜1时的判断方法

1.3 准静态微元过程吸放热的分析归纳

对情况（1）的A→B 过程，情况（3）、（4）、（5）的A→C过程可知，从绝热线上任一点出发的微元过程，如果该过程曲线在绝热线下方，那么该过程对外放热；对情况（1）的A→C过程，情况（3）、（4）、（5）的A→B过程可知，从绝热线上任一点出发的微元过程，如果该过程曲线在绝热线上方，那么该过程从外界吸热.

以上讨论的微元过程，微元曲线或在绝热线上方，或在绝热线下方，即曲线斜率始终小于或大于绝热线斜率.由于绝热线彼此平行，因此沿曲线前进的过程中，曲线依次穿过彼此平行的绝热线，即曲线始终与绝热线相交.

如果曲线某段与某条绝热线相接触后折回，如图6：A→B→C过程，此时热力学曲线与某条绝热线相切与B点，A→B过程在绝热线1下方，对外放热，B→C过程在绝热线2上方，吸收热量，而B点就是吸放热恰好发生转变的位置.

图6 曲线某段与某条绝热线相接触后折回吸、放热判断方法

1.4 小结

经过以上分析归纳可得：从绝热线上任一点出发的微元过程，如果该过程曲线在绝热线下方，那么该过程对外放热；如果该过程曲线在绝热线上方，那么该过程从外界吸热.如果沿曲线前进的过程中曲线不断穿过彼此平行的绝热线，则吸放热情况不变，当且仅当曲线与某条绝热线相切时，吸放热情况恰好在切点处发生变化.

2 理想气体热力学过程整体吸放热的判断

2.1 任意理想气体热力学过程整体吸放热的判断

在分析了微观过程即某点的吸放热情况之后，下面讨论如何根据p－V图像来判断某一个过程的吸放热情况.比如图7中的A－B－C过程.

如图7所示，AE，AD分别为过初始状态点A的等温线和绝热线，由热力学第一定律得

图7 任意的一个热力学过程

其中，WAC在数值上等于曲线AC与横轴所夹面积SAC.下面求ΔUAC.过C点做绝热线交等温线AE于点A′，则A点与A′点在同一条等温线上.因为内能是一个状态函数，所以有

又因为A′C过程沿绝热线，则

想客人之所想，急客人之所急，往往是企业树立良好形象的关键。恰到好处的个性化服务能使顾客真切感受到酒店的关怀，体会到酒店以顾客利益为重，这样友好、周到的酒店形象便可深入人心。

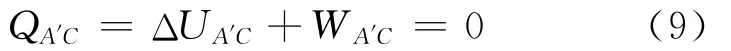
将式（8）和式（9）代入式（7）得

同样，WA′C在数值上等于曲线A′C与横轴所夹面积SA′C.

因此，欲判断AC过程吸放热情况，只需比较AC曲线和A′C曲线与横轴所夹面积SAC和SA′C大小.

如果SAC＜SA′C，该过程放热；如果SAC＞SA′C，该过程吸热；如果SAC＝SA′C，就整体而言，该过程即不吸热也不放热.

这样一来，就把热力学吸放热问题转化为比较区域面积大小，因此只要知道了p－V图上所需区域的面积，吸放热情况就随之确定下来.

值得说明的是，上述提到的判断热力学过程整体吸放热的方法是一个通用方法，可以适用于任何热力学过程.但对于一些比较特殊的热力学曲线，我们还可以通过其他一些比较简便的方法来判断其吸放热情况.

2.2 特殊的热力学过程整体吸放热情况判断

（1）热力学曲线在绝热线一侧体积膨胀时吸放热的讨论（以下推导均假设p（V）是V的单值函数）

我们过初始状态点1做一条绝热线，在绝热线p0（V）上取一点2，使状态2与要研究的末状态3是等体关系，如图8所示.

图8 热力学曲线在绝热线一侧体积膨胀时吸放热的讨论

理想气体的内能U是一个状态量，内能的变化只与初末状态有关，与过程无关，即有下式

又根据公式

得到

对于绝热过程有Q12＝0，又因为V2＝V3，所以式（13）可以写为

Q13的符号取决于这两项：

情况1：当曲线p（V）一直在曲线p0（V）上方，即p（V）－p0（V）恒大于零时，且点3不在点2的下方，可知Q23≥0，进而Q13＞0，该过程吸热；

情况2：当曲线p（V）一直在曲线p0（V）下方，即p（V）－p0（V）恒小于零时，且点3不在点2的上方，可知Q23≤0，进而Q13＜0，该过程放热.

所以，当热力学曲线不穿过初始状态的绝热线时，可以从图像上直接看出该过程吸放热的情况.

（2）热力学曲线末状态在过初始状态的等温线上方的情况

当热力学曲线穿过了过初始状态的绝热线时，根据情况（1）中的推导，该过程的吸放热情况是无法根据上述方法（1）来确定的.但是，当热力学曲线末状态在过初始状态的等温线上方时，如图9所示：

AE为过初始状态点A的等温线，末状态点C在AE上方.由热力学第一定律：

图9 热力学曲线末状态在过初始状态的等温线上方

QAC＝ΔUAC＋WAC以及ΔUAC＞0和WAC＞0得QAC＞0，即该状态吸热.所以，即便所研究过程的热力学曲线穿过了过初状态的绝热线，只要当末状态在过初状态的等温线的上方时，该过程一定是吸热的.

3 结语

经过以上讨论可以得出如下结论：任何一个热力学准静态过程，都可以通过研究其p－V图像来判断其吸放热情况.

对热力学曲线上任意一小段微元过程的研究，可按如下方式进行判断：

从绝热线上一点出发的无穷小微元过程，如果该微元过程曲线在绝热线下方，那么该过程对外放热；如果该过程曲线在绝热线上方，那么该过程从外界吸热.如果沿曲线前进的过程中曲线不断穿过彼此平行的绝热线，则吸放热情况不变，当且仅当曲线与某条绝热线相切时，吸放热情况恰好在在切点处发生变化.

对于热力学过程整体吸放热的研究可通过借助图像面积得到（见图7）：设初始状态A沿着曲线到末状态C，过C点做绝热线交过A点的等温线于点A′，设AC曲线和A′C曲线与横轴所夹面积分别为SAC和SA′C，当SAC＜SA′C，该过程放热；当SAC＞SA′C该过程吸热；当SAC＝SA′C，就整体而言，该过程既不吸热也不放热.

另外对于一些比较简单的热力学过程可直接看出其吸放热情况.

［1］ 刘玉鑫.大学物理通用教程 热学［M］.北京：北京大学出版社，2002：121－157.

［2］ 严子浚.判断热力过程吸热与放热的一种简便方法［J］.物理与工程，2002（3）：16－18.

［3］ 秦允豪.普通物理学教程 热学［M］.3版.北京：高等教育出版社，2011.