一类曲边梯形面积和形心坐标公式的推证与应用
张彦斌, 王慧萍, 杨俊森, 李一帆
(1.河南科技大学 机电工程学院; 2.河南科技大学 土木工程学院, 河南 洛阳 471003)
一类曲边梯形面积和形心坐标公式的推证与应用
张彦斌1, 王慧萍2, 杨俊森2, 李一帆2
(1.河南科技大学 机电工程学院; 2.河南科技大学 土木工程学院, 河南 洛阳 471003)
材料力学课程中,利用图形互乘法计算当弯矩图为曲边梯形情况下梁某截面位置处的变形时,分析计算过程繁琐,学生不易掌握.本文基于积分原理和静矩的性质推导出一种求解曲边梯形面积和形心坐标的公式,并给出两个计算实例.算例表明所提出的计算公式简便、有效,具有一定理论意义和实用价值.
图形互乘法;面积;形心
材料力学是一门理论性较强的技术基础课,是机械、车辆、土木等本科专业必修的学科基础主干课程之一[1-2].由于该课程中公式多,知识点分散,相当一部分学生感觉学起来比较吃力.利用能量法求杆件变形就是材料力学课程的重点和难点之一.而其中图形互乘法是莫尔积分法在诸如梁、刚架等线弹性结构上的应用.图形互乘法之所以比积分法简便省力,其关键在于图形的面积与形心位置已经预先算出,可以直接使用.文献[3]只给出了二次抛物线与直线段围成的曲边三角形的面积与形心位置,而且限定曲线顶点的切线必须平行于基线,而在实际计算中常遇到的是二次抛物线与直线围成的曲边梯形,不能直接使用已有的公式,目前的作法是先将弯矩图分解为若干简单载荷作用下的弯矩图,简单载荷作用下的内力图的面积和形心位置可在文献[3]中查到,然后再使用叠加原理分别进行图乘.缺点在于一是使用者须具备较强的图形分解能力,二是计算过程繁琐,结果易出错.
本文根据积分原理和静矩的性质推导出了二次抛物线与直线段围成的梯形的面积与形心坐标计算公式,且计算公式简单、意义清晰.图形互乘时不需要图形分解,可以直接调用公式计算,过程简便,且结果不易出错.
1 公式推证

图1 曲边梯形图
图 1是由介于二次抛物线 y=ax2+bx+c与基线 Ox所围成的曲边梯形 O1BA2A1,假设二次抛物线左、右端点分别是A1(x1,y1),A2(x2,y2),O1B距离是 h,其中点 C的坐标为(x0,y0),该图的工程背景取自简支梁某一区间典型的弯矩图.O1B边中点的纵坐标,其中当抛物线凸向指向弯矩正坐标方向时,公式第二项前取正号,反之则取负号.现欲推证曲边梯形的面积 ω 和形心 C相对于左端点 O1的坐标 d1(或相对与右端点 B的左边 d2).面积可由积分求出:

欲求 d1,先连接点 A1A2(虚线),则曲边梯形被分成曲边弓形与直线梯形 O1BA2A1两部分,设前者的面积为 ω1,而后者的面积为 ω2,显然

由图 1中的几何关系知,ω、ω1和 ω2间的关系为:而根据文献[4]可知,面积为 ω1的曲边弓形形心的横坐标为,再利用组合图形静矩公式有

将已求得的面积 ω、ω1与 ω2代入式(3)并化简整理得:

式(4)和(5)确定了曲边梯形的形心位置.
2 算例分析
算例 1 已知抗弯刚度 EI为常数的简支梁承受荷载如图 2a所示,试求:截面 B的转角.
解 先求出 A、B两点处的支反力,并画出梁的原有荷载弯矩图 Mp(图 2b),以及在 B点处加单位力偶后的单位载荷弯矩图 M(图 2c).并在 CB、AC两段进行图乘运算.
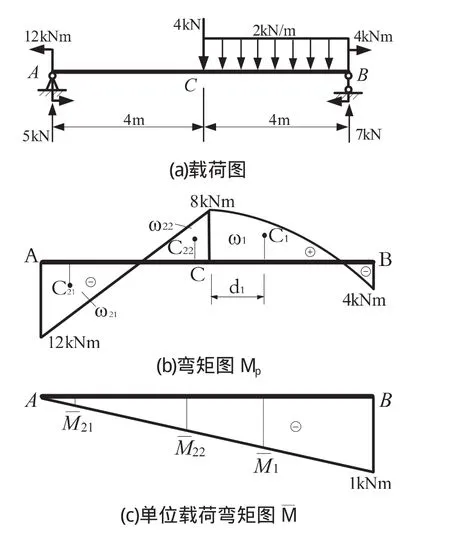
图2 算例1图
由前面导出的公式可方便地求得CB段荷载弯矩图中点纵坐标 y0,面积 ω 和形心 C1相对左端点的坐标 d1,进而得到该部分原载荷图形的形心 C1所对应的单位载荷弯矩值,即

AC段的原载荷弯矩图为一斜直线(见图 2b),可按文献[3]提出的方法再分段,则两部分的面积和形心坐标分别为

将所得到的参数代入得
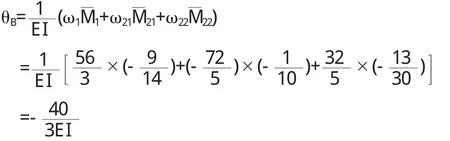
由于计算结果显示 B截面处转角 θB为负值,这说明其逆时针转动.
算例 2 已知抗弯刚度 EI为常数的简支梁承受荷载如图 3a所示.求:截面 B的转角.
解 首先求出点 A、C处的约束反力,然后作出原载荷弯矩图 Mp(图 3b)和在截面 B施加单位力偶的弯矩图 M(图3c).将在 AB、BC两段进行图乘运算.则有
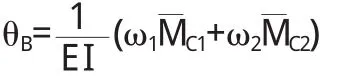
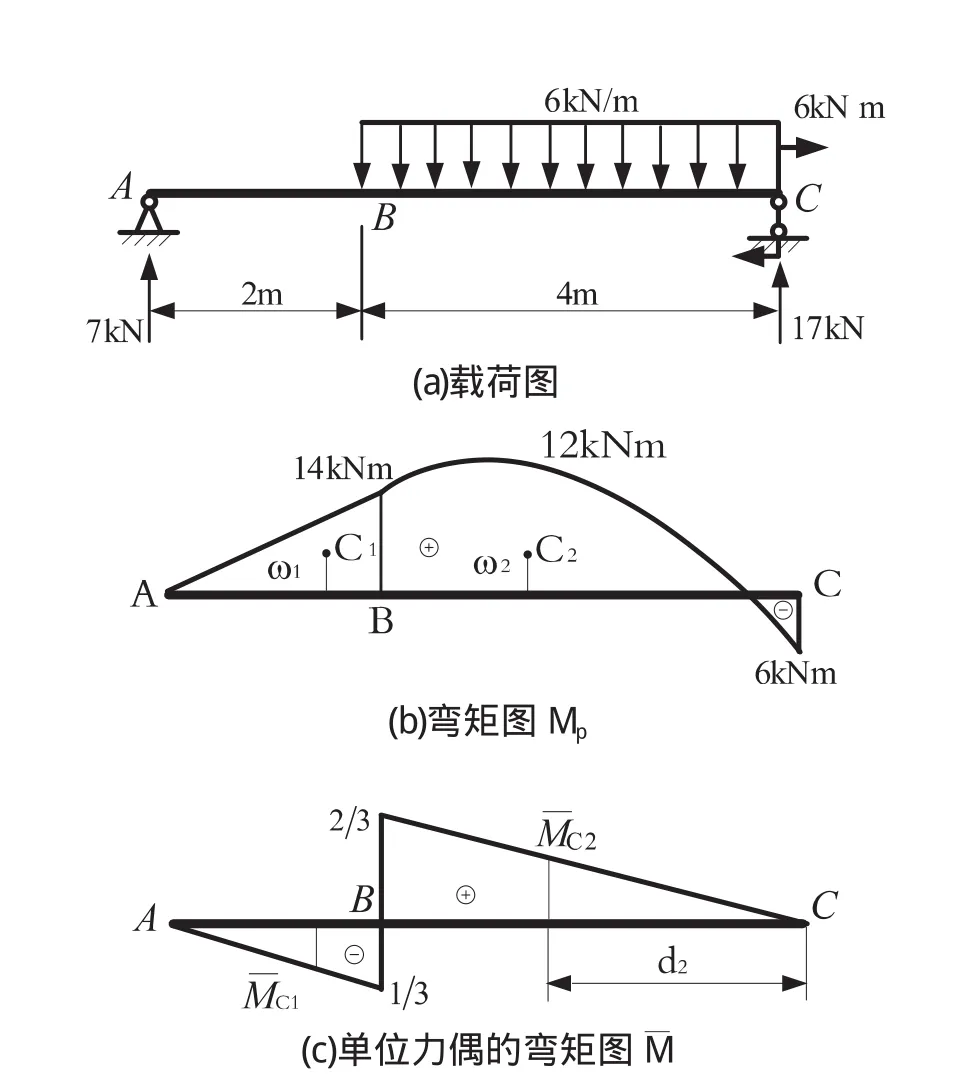
图3 算例2图
式中 ω1、ω2分别为 AB、BC段原载荷弯矩图的面积,而MC1、MC2为其原载荷图形心对应的单位载荷值.容易求得

由本文导出的公式可方便地求得BC段荷载弯矩图中点纵坐标 y0,面积 ω2和形心相对于右端点 C点的坐标 d2,从而可得到该部分原载荷图形的形心所对应的单位载荷弯矩值 MC2,即

将以上所有参数代入转角 θB的计算公式得
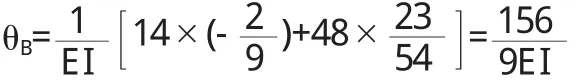
由于计算结果显示 B截面处转角 θB为正值,这说明其顺时针转动.
3 结束语
图乘法是材料力学课程中用于求解受载构件变形的一种重要方法.如何确定复杂问题弯曲图的形心位置是解决此类问题的关键,本文推导出了一种简单实用的公式.算例表明,应用所推导的公式进行构件变形计算,简化了运算程序,降低了分析难度,不失为一种有效的算法.
〔1〕王放,陈志谦.《材料力学》课程教学改革与实践[J].西南师范大学学报,2011,36(2):206-210.
〔2〕刘桂荣,韩立新.“材料力学”教学方法探索[J].中国电力教育,2011(25):114-119.
〔3〕单建,吕令毅.结构力学[M].南京:东南大学出版社,2011.
〔4〕刘鸿文.材料力学[M].北京:高等教育出版社,2011.
O172.2
A
1673-260X(2014)08-0009-02
河南科技大学教学改革计划重点资助项目(2009Z-028)

