电涡流位移传感器测量模型及其在叶尖间隙测量中的空间滤波效应
胡天林,谢海鹤,颜黄苹,黄元庆
(厦门大学物理与机电工程学院,福建 厦门361005)
在压气机、汽轮机和涡轮机等旋转叶片设备中,叶尖与机匣的间隙动态监测及控制非常重要.叶尖间隙的大小是影响设备运行效率、结构安全和使用寿命的重要参数[1].大型涡轮机中,叶尖间隙减少0.025 mm,其效率将提高0.1%[2].叶尖间隙大小既要保证叶片与机匣不发生刮擦,也要防止间隙过大导致效率降低[3].通过传感器对叶尖间隙的实时在线测量,根据叶轮运行状态信息实现对叶尖间隙的闭环控制.叶尖间隙测量获得的叶片振动参数,也可以为故障诊断(外来物、累积损伤、裂缝增长、转子不平衡、叶盘不完整等)提供依据[4-7].目前叶尖间隙传感器测量主要有电容传感器、电涡流位移传感器、光纤传感器、微波传感器、激光多普勒效应传感器[8].根据电磁原理,导体位于交变的磁场时,导体中将产生呈涡流状的感应电流,该效应为涡流效应.电涡流位移传感器具有非接触、操作方便的特点,作为叶尖间隙测量的常用传感器,研究其在叶尖间隙测量中的影响具有重要意义.通过建立电涡流位移传感器有限元测量模型,分析叶片尺寸、传感器敏感区、转速和采样速度等与空间滤波效应的关系及对叶尖间隙测量结果的影响,为后续叶片振动、转子平衡等实验研究提供理论依据.
1 电涡流位移传感器测量模型
1.1 电涡流位移传感器模型的建立
电涡流位移传感器由探头线圈、电缆、前置器及被测体构成[9],如图1所示.其基本测量原理是线圈与被测物体的距离变化,将引起线圈品质因数变化,进而导致振荡信号变化.通过前置器归一到电压或电流信号.常用的电感值测量方法有调幅法和调频法两种.文献[9]对该模型进行详细的分析,等效品质因素如公式(1)所示:

其中,d为检测距离,μ为被测体磁导率,ρ为被测体电阻率,fa为激励频率.由于被测体是固定的,激励频率也是固定的,在理想温度情况下,影响测量结果的主要因素是距离.
实际上被测体的形貌不是理想的平面,或者在测量过程中其面积不符合电涡流测量面积要求,也会引起测量值的变化,即电涡流位移传感器存在空间滤波效应影响.因此实际的电感品质因数影响函数表示为:

其中,S是电涡流测量绝对面积,d是线圈与被测体的距离.面积越大,涡流线圈的互感影响越大,因此测量体的面积对电涡流线圈互感系数的影响成正比(在互感线圈敏感区范围内);距离越大,涡流线圈的互感越小,因此距离对电涡流线圈互感系数的影响成反比,采用以下公式描述:

图1 电涡流位移传感器测量原理及等效电路图Fig.1 Eddy current sensor operating principle and the equivalent circuit

其中S是有效互感面积;d是被测体与线圈互感距离;εr是相对影响系数,可由实验确定.叶尖间隙涡流传感模型,就是叶片上每个面积元与传感器敏感区构成的一个等效互感线圈,如图2所示.由于传感器敏感区是固定的,而叶片的面积是动态变化的,因此将叶片的面积分解为微小的多个面积元形式.将叶片面积元在传感器敏感区上的投影作为单个有效面积,所有投影面积的叠加视为涡流效应的作用面积,其表达式可以表示为

Si表示叶片面积元的矢量值、s0表示传感器面积方向单位矢量,di表示面积元与传感器的距离.采用矢量形式可以更好的描述叶片面积元在传感器敏感区的投影.Si×s0结果为负,表示该叶片面积元正对传感器;否则是背对传感器,如图3所示.若传感器有效面积太小,根据输出解调电路特性,传感器处于饱和状态.传感器达到有效面积后,传感器信号与面积成线性递减关系,直致有效面积达到饱和.因此有效的面积元条件
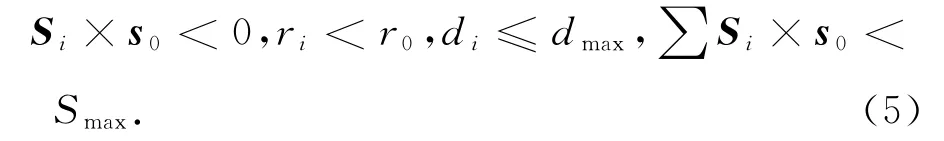
它需满足公式(5)条件:Si×s0结果为负;面积元处于传感器敏感区域内,即面积元与敏感区轴心的距离ri小于敏感作用范围r0;面积元与传感器敏感区的距离di在传感器的测量范围dmax内;面积和不能大于总的敏感面积.根据公式(4)、(5)可以计算出叶片引起的总涡流值变化.
1.2 叶片三维矢量模型的建立
为了精确分析涡流位移传感器在叶片旋转情况下的信号变化,需要充分考虑叶片的形状及其与传感器的相互作用.根据有限元原理,叶片可看成由面积元构成,将所有面积元引起的传感器电感Q值变化累加作为整体涡流效应,建立简易的叶片模型,如图4所示.在笛卡尔坐标系下,叶片模型单面面积元的坐标关系如下:


图2 互感面积等效电路Fig.2 Equivalent circuit of mutual inductance area
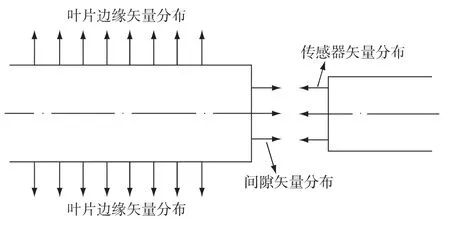
图3 叶片和传感器矢量分布示意图Fig.3 Vector of blade and senor
其中α0为叶片初始倾角,α为叶片最终倾角,r0为叶盘半径,l为叶片长度.同理建立另一面积元坐标和叶片端面面积元坐标,获得单个叶片的总坐标fb(x,y,z),并将其转换成柱坐标后旋转,这样可以确定整个叶片总轮廓矩阵ft(th,r,z).

图4 叶片模型示意图Fig.4 Blade model
鉴于轮廓矩阵不能反映叶片面积元与传感器的矢量作用效果,在此基础上建立了具有矢量方向的轮廓矩阵fb(x,y,z,kx,ky,kz),如图5所示,通过矢量乘积可获得每个面积元与传感器的作用效果.
2 电涡流位移传感器空间滤波特性
2.1 电涡流位移传感器的模型验证
以PD6-S2.5GIU2涡流传感器为例,验证有限元模型的正确性.该传感器外径是6.5mm,为电流调理输出.该传感器的调理电路特性是:在线性范围内,其输出电流大小与距离成正比,与面积成反比.首先测量传感器的线性,采用厚度为8mm的铝合金矩形叶片,实验获得如图6所示的数据,对其拟合,电流与位移关系如公式(6)所示.

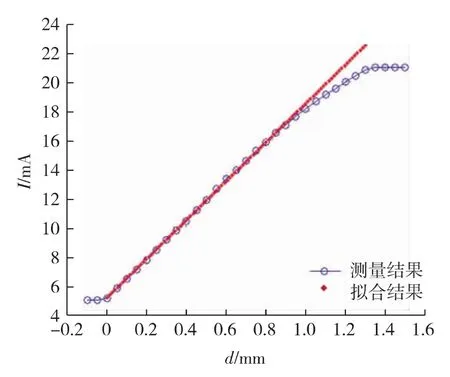
图6 涡流传感器线性测量Fig.6 Linear measurement of eddy senor
其中,d是位移,单位是 mm.结合公式(4),(7),本实验采用的传感器可用公式(8)的数学模型表示.
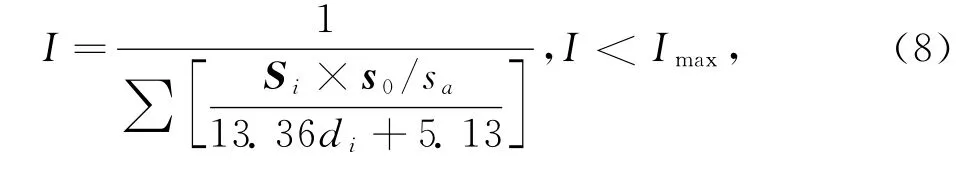
其中I是涡流传感器输出电流,单位是mA,d是间隙,单位是mm.
传感器沿着平行于叶片平面方向移动,即可测定不同面积下的涡流传感器信号变化.采用厚度为8 mm的叶片进行旋转扫描,最小距离是0.17,0.48和0.82mm,获得电流变化值,测试如图7所示点画线,根据公式(8)的数学模型获得理想曲线如图7所示的实线.从图7可以看出,理论分析与实验曲线基本一致,其差别主要是由于对有效面积的计算采用的是理想测试距离和面积,实际上在测试距离外或理想测试面积外,也有一定的涡流效应,因此存在一定误差.

图5 叶片矢量模型Fig.5 Vector model of blade

图7 涡流传感器公式仿真与测试曲线Fig.7 Simulation of eddy senor and measurement curve
2.2 敏感区引起的空间滤波效应
采用长度为141mm、厚度为8mm的铝板作为叶片,基座半径15mm,进行旋转空间滤波效应研究.采用上述模型分析,测试数据和理想曲线如图8所示,通过面积、距离参数建立的的电涡流位移传感器有限元模型测试的数据与实际比较符合,因此该模型是合理的.从图8上还可以看出,原来尖锐的叶尖变化.由于电涡流传感器的敏感区较大而变得光滑,这是敏感区较大的传感器的空间滤波效应,因此这种传感器不适用于具有突变特性的叶尖测量.
2.3 采样速率及转速引起的空间滤波效应
由于传感器的采样速率有限,加上叶片高速旋转,必然造成叶尖间隙采样率的降低,相当于一个低通滤波器.设传感器的采样速率是fs,叶片转速是n(r/min),单位采样时间内叶片转过的弧度是

弧度分辨率是由转速和采样速率决定的.如图9所示,若采样速率过低或转速太快,则空间分辨率就会降低.设叶片厚度为w,则对应的弧度大小hrad≈只有满足条件Δrad<hrad,才能保证叶片单次循环一圈传感器能测量到至少一次叶尖间隙.弧度分辨率过低相当于空间滤波效应,造成所测的叶尖间隙与实际不符.弧度分辨率越高,叶尖间隙变化测量值越准确.

图9 不同转速下叶尖间隙采样对比Fig.9 Values of tip clearance in different speed
3 结 论
本文建立了叶片矢量模型,基于模型分析了电涡流位移传感器在叶尖间隙测量中的滤波效应.分析结果表明,传感器的感应区域直径至少要小于叶尖最小宽度的0.7倍,才能保证叶尖间隙能比较准确的测量出来;同时空间角分辨率满足Δrad<hrad,是保证叶尖间隙在单次旋转过程中能被传感器测量到的必要条件,Δrad值越小,测量的叶尖间隙数据越准确.上述分析结果为后续测量叶片到达时间、转子平衡等实验研究搭建提供了理论依据.

图8 电涡流位移传感器测量实验装置(a)、理想曲线与测试曲线(b)Fig.8 Experiment of eddy sensor measurement(a),ideal curve and real curve(b)
[1]Jang C M,Gukano T,Furukawa M.Effects of the tip clearanceon vertical flow and its relation to noise in an axial flow fan[J].JSME International Journal,2003,46:356-365.
[2]Wiseman,M W,Guo T.An investigation of life extending control techniques for gas turbine engines[C]∥Proceedings of the American Control Conference.Arlington,VA:IEEE,2001,5:3706-3707.
[3]El-Batsh H M,Hanna M B.An investigation on the effect of endwall movement on the tip clearance loss using annular turbine cascade[J].International Journal of Rotating Machinery,2011(2011):489150.
[4]Tappert P,von Flotow A,Mercadal M.Autonomous PHM with blade-tip-sensors:algorithms and seeded fault experience[C]∥Aerospace Conference Proceedings.Big Sky,MT:IEEE,2001,7:3287-3295.
[5]Woike M R,Abdul-Aziz A,Bencic T J.A microwave blade tip clearance sensor for propulsion health monitoring[R].Washington D C:NASA,2010.
[6]Beauseroy P,Lengelle R.Nonintrusive turbomachine blade vibration measurement system[J].Mechanical Systems and Signal Processing,2007,21(4):1717-1738.
[7]Lawson C P,Ivey P C.Tubomachinery blade vibration amplitude measurement through tip timing with capacitance tip clearance probes[J].Sensors and Actuators A,2005,118:14-24.
[8]Holst T A.Analysis of spatial filtering in phase-based microwave measurements of turbine blade tips [D].Atlanta:Georgia Institute of Technology,2005.
[9]于亚婷.与被测材料无关的电涡流位移传感器基础理论与实现方法研究[D].成都:电子科技大学,2007.
——以赣州市龙南县为例

