基于l1正则化的匀速运动模糊图像复原

洪景新，陈 栩

（厦门大学信息科学与技术学院，福建 厦门361005）

由于受到成像系统本身的缺陷、成像过程中传播介质的杂质，以及相对运动的变化等因素的影响，图像信息的采集过程难免会对图像信息造成某些失真和不同程度的降质，这一现象称为图像退化.利用数字图像处理技术，对退化图像加以改善并复原原图像信息，这个过程就称为图像复原.如今众多的应用领域对图像质量的要求都相当高，尤其对精度和清晰度的要求，因此图像的复原问题愈加具有意义.

复原技术是基于将退化过程模型化并采用逆过程处理模糊图像，实现图像的复原.逆滤波算法［1］是最早用于图象复原的一种标准技术，该算法容易受到噪声的干扰，噪声较大时，图像恢复的效果很差.随后，Helstrom［2］采用最小均方误差估计方法，提出了基于维纳滤波器的滤波算法，该方法只能针对某个具体图像设计最优滤波器，对于其他图像则不一定能达到较好效果.Hunt和Andrews［3］对逆滤波、维纳滤波进行了对比研究，并提出了约束最小二乘滤波方法，这是一种基于线性表达的恢复方法，对各种退化图像的恢复具有较好的适应性.近几年，也出现了将稀疏表示［4］运用到图像复原中的研究，使模糊图像的恢复效果不断改善.

本文首先阐述图像复原的一般退化模型与匀速运动的特性，从中推导出匀速运动模糊的退化矩阵.然后，从求解大型线性方程组的角度，分析常见的约束最小二乘滤波算法存在的问题，说明l1正则化在图像复原上的优势，提出一种基于l1正则化的复原算法，并利用基追踪算法对正则化问题进行求解.最后对不同模糊尺度的图像进行仿真实验，大量的实测数据和图像表明，本文算法对较宽范围的模糊尺度都有着很好的复原效果，同时能有效抑制振铃效应.

1 模糊图像退化模型

1.1 一般退化模型

一般退化过程可以建模为一个退化函数和一个加性噪声项的级联［1］，其退化模型可以表示为：

其中，y，x∈Rm分别为模糊图像和原图像，H∈Rm×m是退化过程的表示矩阵，n∈Rm为退化过程中的加性噪声.不考虑加性噪声时，退化模型可简化为：

此时，模糊图像y∈Rm可看作是原图像x∈Rm在H下的线性投影，而图像去模糊的过程就是在退化函数H∈Rm×m已知或可测量的前提下，从模糊图像y∈Rm中求解未知的原图像x∈Rm.因此，去模糊的过程等价于求解线性逆问题，也可理解为从模糊图像重构出原图像的过程.

1.2 匀速运动模糊图像退化模型

运动模糊，是图像退化的一个主要形式，是由于在图像信息采集时，目标物体与成像装置的相对位移而产生的一种退化问题，例如在运动物体上（飞机、宇宙飞行器等）拍摄外界的照片或拍摄高速运动物体的照片均存在运动模糊问题.

匀速运动模糊是最基本的运动退化，各类复杂的运动退化模型可分解为多个匀速运动退化模型.假设成像时间T内，目标物体与成像装置以匀速v做相对运动，选取图像中一行像素点g（i），i＝0，1，…，n，将成像时间T划为L个等长的单位时间t，且在0时刻，令物体上点f（0）投影在像素点g（0）上，若目标物体每单位时间移动一个像素，则kt时，物体上点f（0）的投影位置为像素点g（kt）.由此不难看出，每个像素点接受的信息为成像时间内物体移动范围的各点的加权平均，即：

其中，L即模糊尺度.令模糊路径上的点扩散函数为：

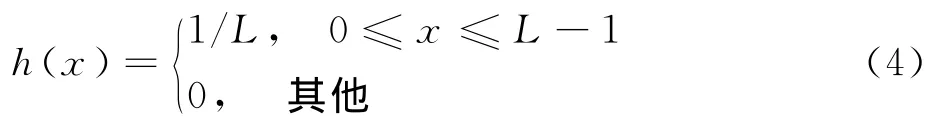
则式（3）可写成离散卷积的形式：

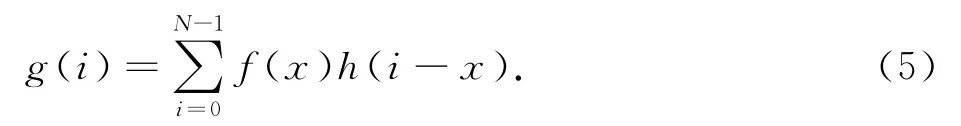
若用矩阵形式表达，即可得到退化矩阵：

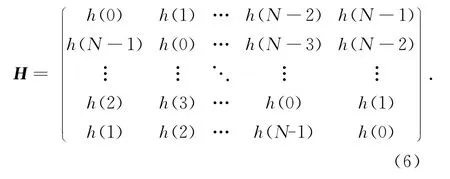
2 l1－min图像复原算法

2.1 约束最小二乘算法

求解线性方程的过程就是求解最小二乘问题.常见的最小二乘算法［5］是求解线性逆问题的经典算法，其中心思想是通过最小化估算数据与实际数据之间的误差的平方来寻找问题的最优解，其函数表达式为：

在图像复原中，矩阵H∈Rm×m一般是病态的，最小二乘的解对误差（舍入误差或其他误差）很敏感，导致求得的解往往不是理想的，进而使得复原效果很差，最小二乘也因此变得没有意义.为了解决这个问题，可通过正则化来约束最终的解.

正则化的基本思想是用一族与不适定问题有着近似解的适定问题来逼近原问题.选择合适的正则化方法，可确保我们得到理想的解.约束最小二乘算法中通常采用Tikhonov正则化，对式（7）进行Tikhonov正则化可得：

式（8）即为常见的约束最小二乘算法.式中第一项为残差约束项，用以控制解的逼近程度，第二项为正则约束项，用以约束信号的能量.正则参数λ＞0用于平衡精确度与噪声敏感度.L是微分算子，一般选用拉普拉斯算子.约束最小二乘算法属于基于l1范数的正则化，实践表明，当方程y＝Hx中的矩阵H与向量y有扰动时，约束最小二乘法的解往往不稳健.

2.2 l1 正则化

l1正则化是采用l1范数作为了约束条件，来求解最小二乘问题的正则化方法.因此用l1范数作为能量约束取代式（8）中的正则约束项，则可以得到：

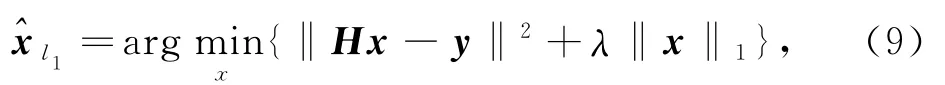
其中，l1正则约束项是稀疏约束条件.l1范数指是向量中各元素的绝对值之和，若个别元素出现扰动，对整体影响相比l2范数较小.因此，不同于基于l2的正则化形式，基于l1的正则化对异常值较不敏感［6］.在图像处理中，色块之间往往有尖锐的边缘，会出现突变的异常值，因此基于l1的正则化更适用于图像处理.但同时，由于l1范数的稀疏约束条件，使得求解出来的x∈Rm变稀疏.而对于图像这类自然信号来说，几乎所有的像素灰度值都是非零的，所以要对图像进行稀疏变换.

图像的稀疏表示是基于 Mallat等［7］提出的信号在过完备库上的分解.根据稀疏表示理论，若存在一个过完备字典W，使图像或信号可以表示为：

若向量α∈Rm中只有很少的大系数，则称图像或信号x∈Rm是可稀疏的.若α∈Rm只有K个非零元素，则称α∈Rm为图像或信号的K稀疏表示.因此，式（9）可转化为：

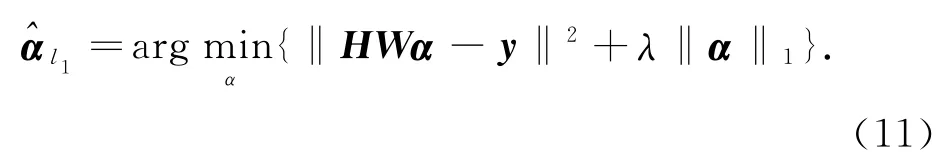
常见的稀疏变换有傅里叶变换、离散余弦变换（DCT）、小波变换等.本文采用DCT变换对图像进行稀疏表示.

3 基追踪算法

基于l1正则化的线性规划问题的常见求解方法有基追踪（BP）算法和迭代阈值算法（IST）等，本文选用BP算法进行求解.

BP方法［8］是Chen等提出的一种信号稀疏表示法.它寻求从过完备的函数（基）集合中得到信号的最稀疏的表示，即用尽可能少的基尽可能精确地表示原信号，从而获得信号的内在本质特性.

BP算法的思想是通过极小化l1范数来获得最稀疏的解.即求解下式：

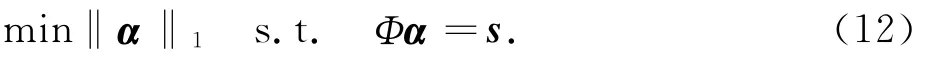
由文献［9］可知，极小l1范数最优问题与线性规划问题等价.可通过等价变换m⇔2n；x⇔（u，v）；c⇔（1，1）；A⇔（Φ，－Φ）；b⇔s，使其重构成如式（13）所示的标准线性规划问题：

其中，x∈Rm是一个重新定义的向量.因此，BP问题的解可以通过求解线性规划问题来获得.线性规划问题的通常解法有单纯形法、内点法.本文采用基于内点法的原－对偶障碍算法（primal－dual log－barrier algorithm）求解线性规划问题：

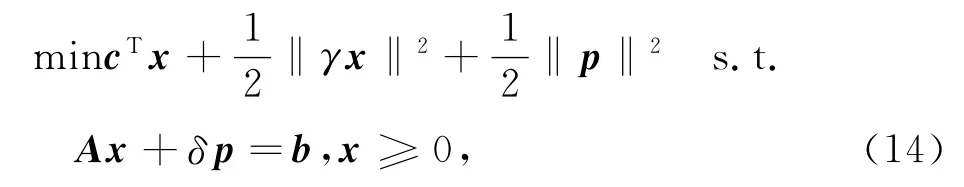
其中，γ和δ为正则化系数，在不同的实际问题，对其进行相应的初始化.对于正则化形式如式（14）的线性规划问题，原－对偶障碍算法的求解流程图如下：

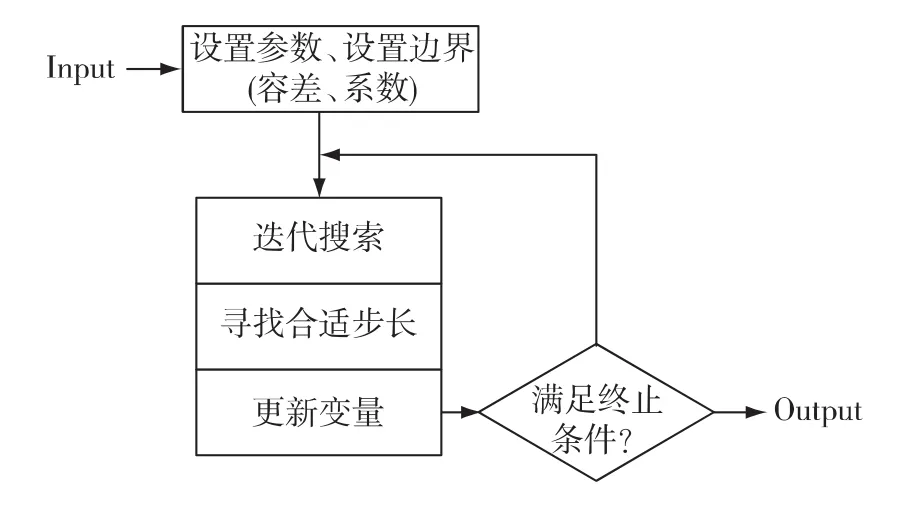
图1 原－对偶障碍算法流程Fig.1 The flow chart of primal－dual log－barrier algorithm

原－对偶障碍算法的具体算法步骤如下：

Step 1：设置参数：可行性容差FeaTol、对偶间隙容差PDGapTol和正则化系数γ，δ.

Step 2：设置边界：x＞0，y，z＞0，μ＞0，初始化k＝0.

Step 3：循环：

（i）t＝c＋γ2x－z－ATy，r＝b－Ax－δ2y，v＝μe－Zx，D＝（X－1Z＋γ2I）－1，其中，X，Z是分别由x，z构成的对角矩阵，e是单位向量.

（ii）从（ADAT＋δ2I）Δy＝r－AD（X－1v－t）中求解Δy，并计算

Δx＝DATΔy＋D（X－1v－t），

Δz＝X－1v－X－1ZΔx.

（iii）计算原步长和对偶步长ρp，ρd并更新变量

ρp＝0.99×max｛ρ：x＋ρΔx≥0｝，

ρd＝0.99×max｛ρ：z＋ρΔz≥0｝，

x＝x＋ρpΔx，y＝y＋ρdΔy，z＝z＋ρdΔz，

μ＝（1－min（ρp，ρd，0.99））μ.

（iv）k＋＋.

Step 4：终止条件：

4 实验设计与结果分析

为了验证l1－min图像复原算法对匀速运动模糊图像的去模糊效果，本文从视觉效果和客观指标评价两方面设计实验，并选用经典维纳滤波算法和约束最小二乘算法进行比较.实验中，图像选择分辨率为256×256的标准灰度图片，根据匀速运动图像退化模型，生成退化矩阵分别对图像进行退化处理.模糊尺度L＝50的退化效果如图2所示：

图2 实验图像和水平运动模糊退化图像Fig.2 Original image and horizontal motion－blurred image

4.1 视觉效果

图3为标准Lena和Peppers图像在模糊尺度L＝50下3种算法的复原图像.图4为标准Cameraman图像在不同模糊尺度下本文算法的复原图像.从图3实验结果可以清楚看到，3种复原算法都使图片质量相比退化图像得到一定的改善.显然，维纳滤波图像效果最差，图像模糊严重，可以看到很多重影.最小二乘算法与l1－min算法的恢复图像较为清晰.不过，从放大图像可看出，最小二乘算法的恢复结果带有振铃现象，而本文算法恢复的图像在完整地保存了边界信息的同时几乎看不出振铃现象.从图4实验结果可以看出，本文算法在不同模糊尺度下，都有良好的复原效果且随模糊尺度的增长，复原效果只有少量下降.

图3 不同算法的复原效果对比，模糊尺度L＝50Fig.3 Restoration comparison of different algorithms with blur length of 50

图4 不同模糊尺度下本文算法复原效果对比Fig.4 Restoration comparison of the proposed algorithm with different blur length

4.2 客观指标评价

客观指标评价选取灰度平均梯度值（gray mean grads，GMG）［10］和结构相似指数（structural similarity index measurement，SSIM）［11］作为衡量复原图像的标准.GMG属于无参评价，它能较好反映复原图像的对比度和纹理变化特征，其值越大表示图像越清晰，图像质量越好.SSIM是有参评价，它可以衡量复原图像与原图像的相似度，其值越高表示2幅图像越相似.

图5为标准的Peppers图片，在不同退化程度下，3种算法的复原图像的评价指标对比.其中，本文算法与最小二乘算法默认迭代20次.图中的实测数据可以看出，3种算法下复原图像相比退化图像的客观指标都有所提高，l1－min图像复原算法在各退化程度下的两种指标都优于其他算法.在不同模糊尺度下结构相似指数SSIM表明l1－min图像复原算法的复原图像在结构上比其他算法更相似性于原图.而在GMG上，本文算法复原图像的清晰度的优势更大.其中维纳滤波算法随模糊尺度的增长GMG值逐渐降低，而本文算法与最小二乘算法随模糊尺度的增长相对比较稳健，但l1－min算法明显维持在更好的水平上.

图5 实验中不同算法的评价指标Fig.5 Evaluation criteria of different algorithms in experiment

5 结 论

本文在最小二乘算法的基础上，用l1范数代替l2范数，再引入BP算法精确求解l1正则化的线性规划问题，提出一种基于l1－min的匀速运动模糊图像复原算法.算法对较宽的模糊范围下的退化图像都可以获得一个较清晰的图像复原效果，且能有效抑制约束最小二乘算法中的振铃现象.但在个别特殊模糊尺度下，算法恢复出来的图像的质量突降，如图4中模糊尺度80下的复原图像中出现的波纹现象.因此认为下一步工作应探讨和研究这些特殊模糊尺度导致图像质量下降的原因，争取改善图像质量.

［1］Gonzalez R C，Woods R E.冈萨雷斯数字图像处理［M］.北京：电子工业出版社，2003.

［2］Helstrom C W.Image restoration by the method of least squares［J］.JOSA，1967，57（3）：297－303.

［3］Andrews H C，Hunt B R.Digital image restoration［M］.New York：Englewood Cliffs，1977.

［4］Zhang H C，Yang J C，Zhang Y N，et al.Sparse representation based blind image deblurring［C］∥IEEE International Conference on Multimedia and Expo（ICME）.Barcelona，Spain：IEEE，2011：1－6.

［5］Bjorck A.Numerical methods for least squares problems［M］.Philadelphia：Society for Industrial and Applied Mathematics（SIAM），1996.

［6］Beck A，Teboulle M.A fast iterative shrinkage－thresholding algorithm for linear inverse problems［J］.SIAM Journal on Imaging Sciences，2009，2（1）：183－202.

［7］Mallat S G，Zhang Z.Matching pursuits with time－frequency dictionaries［J］.IEEE Transactions on Signal Processing，1993，41（12）：3397－3415.

［8］Chen S S，Donoho D L，Saunders M A.Atomic decomposition by basis pursuit［J］.SIAM Journal on Scientific Computing，1998，20（1）：33－61.

［9］Bloomfield P，Steiger W L.Least absolute deviations：theory，applications，and algorithms［M］.Boston：Birkhäuser，1983.

［10］袁万立.模糊图像复原及评价方法的研究［D］.无锡：江南大学，2012.

［11］Wang Z，Bovic A C，Sheikh H R，et al.Image quality assessment：from error visibility to structural similarity［J］.IEEE Transactions on Image Processing，2004，13（4）：600－612.