基于分形维数的光学表面质量评价及响应曲面模型
董之然,杨 炜
(厦门大学物理与机电工程学院,福建 厦门361005)
在航天、军事、日常生活领域中,光学元件在各种精密光学系统中的应用日益广泛,对光学元件的表面精度要求也越来越高.在现有方法中,多采用统计学标准参数,如用峰谷(PV)值、均方根误差来反映光学元件的表面形貌[1],但是光学元件表面的微观形貌结构呈现出随机性、无序性和多尺度性特征,反映出的是一种非平稳的随机过程,对于同一光学表面,不同的采样长度、仪器分辨率和测量方法所测出的统计参数值是不同的[2].大量研究表明:光学元件表面具有统计学上的自相似性结构[3],在一定尺度范围内具有分形特征,而分形几何理论对描述具有标度律特征的自然现象具有很好的适用性.因此,本文采用结构函数法计算化学机械抛光(chemical mechanical polishing,CMP)加工后光学元件表面的分形维数,同时分析了分形维数与表面传统评价参数PV值近似线性的关系,验证了可以用分形维数来评价光学元件表面形貌.
其次,对于如何提高CMP光学元件的表面精度,国内外学者观点较为统一,都是采用控制抛光压力、抛光盘和工件相对转速2种参数来实现,但是对于这2个因素何者更显著影响精度鲜有报道.因此,本文提出了建立分形维数与抛光参数的响应曲面回归模型,评价各抛光参数对分形维数的影响权重,旨在通过控制显著性较强的抛光参数来获取更好的光学元件表面质量.
1 分形维数计算方法
分形几何理论是研究和处理具有标度率特征不规则图形的强有力工具[4],其重要参数“分形维数D”能完全地表达出光学元件表面所有的微观结构信息,是一种描述微观轮廓的有效手段.分形维度常用计算方法有尺码法、盒计数法、方差法、功率谱法和结构函数法等[5].尺码法和盒维数的计算结构与理论维数相差太大,方差法抗干扰性差,功率谱法的本质是傅里叶变换,计算过程存在许多近似,精度不高,因此在工程运用中,多采用结构函数法来计算分形维数.结构函数法直接使用表面高度数据,能比较真实地反映光学元件的微观结构.
结构函数法是将表面轮廓曲线视为一个空间序列Z(x),则它具有分形特征的光学元件表面轮廓曲线采样数据,其结构函数满足[6]
其离散表达式为
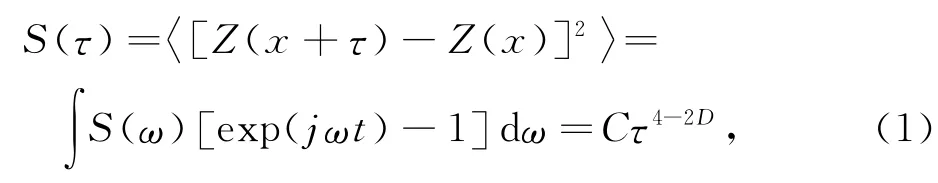

式中,τ为尺度;X[i]为测量轮廓高度;N为采样点数;n为i的任意增量;G为形貌特征参数.
根据已知轮廓高度数据,求出结构函数S(τ),在双对数logS(τ)-logτ坐标中用最小二乘法进行拟合,得到直线斜率α,则分形维数可表示为:

2 光学表面分形维数计算
为了研究光学元件表面分形特点,寻找分形维数与PV值的关系,本文设计了光学元件CMP实验来验证分形维数评价光学元件表面形貌的可行性,实验条件如下:POLI-400CMP抛光机,主要包括夹持工件的抛光头、抛光盘、抛光液喷射装置等部件,如图1所示,抛光加工材料为JGS1、K9光学玻璃,采用120nm SiO2CMP抛光液,抛光机可控参数为抛光压力P和转速V(文中的转速均为抛光盘和工件相对转速).基于2个可控参数,设计一个二因素三水平的完全因子实验,参数具体设置如表1所示.抛光完成后,利用Taylor Hobson 1240轮廓仪(测针长度为60mm,分辨率为0.8nm)对光学元件表面轮廓进行测量(采样长度为10mm,采样间隔为0.125μm,共采集80 000个数据点),从而得到PV值,最后采用结构函数法计算出分形维数,实验结果如表2所示.

图1 POLI-400CMP抛光机Fig.1 POLI-400CMP polishing machine
图2为JGS1、K9光学玻璃CMP加工后的轮廓曲线,根据轮廓曲线上的采样数据,利用式(2)计算出结构函数S(τ)与尺度τ的双对数曲线,分别如图3所示.可以看出,抛光表面存在一个有限界定尺度nc,在一定的尺度范围内,结构函数主要由工艺参数决定[7],结构函数与尺度具有良好的线性关系,存在明显的分形特征.但超出这个范围后,微观轮廓相互作用减弱,工艺参数的作用减弱,其他外界干扰因素对表面轮廓的影响逐步明显,使得结构函数与尺度呈现出非线性的关系.

表1 CMP抛光实验参数设置Tab.1 CMP polishing experiment parameter settings

表2 光学玻璃不同轮廓线的分形维数Tab.2 The fractal dimension of the profile of optical glass is different

图2 JGS1,K9光学玻璃的表面轮廓曲线Fig.2 GS1,K9optical glass surface profile curve
通过实验,可以看出JGS1、K9光学玻璃表面的分形维数具有以下特征:
1)分形维数不受采样长度的影响,分形维数包含光学元件表面的所有结构信息,是光学表面信息的一个固有特性,具有尺度不变性的特征,适合所有测量尺度下运用.
2)采样点数数量对分形维数有一定的影响,如图3所示,分形维数是通过结构函数法计算求得的,大量的测量数据点会降低计算误差,会使结构函数与尺度的关系趋于稳定,提高分形维数计算值的稳定性;相反过于少量的数据使得结构函数与尺度的线性关系不明显,分形维数容易受到测量仪器、外界环境的干扰因素的影响,分形维数计算值产生较大误差,根据文献[8-10],每毫米采样长度的采样点数一般都要在1 000个以上为宜.

图3 JGS1,K9的双对数曲线Fig.3 The double logarithmic curve of JGS1,K9
3)分析表2中PV值和分形维数的关系可以看出,PV值与分形维数存在一定的近似线性关系,PV值反映的是光学元件表面微观轮廓的幅值参数,而分形维数反映的是表面间距和幅值的综合参数,使得这种线性关系并不确定.PV值越小,所对应的分形维数的值就越大,分形维数值越大,表面轮廓越复杂,微观结构越精细,表面越光滑,质量越好,所以当PV值小且分形维数大时,可认为表面质量较高.
3 抛光参数与分形维数的关系
为了更好地指导加工,在分析了分形维数与PV值的基础上,需研究抛光参数对分形维数的影响权重,为此,利用上述实验数据建立抛光参数与分形维数的响应曲面回归模型.
响应曲面法,也称为回归设计,这类实验设计主要是寻找实验指标与各因子间的定量规律,并建立响应曲面回归模型[11].与多元线性正交设计、正交多项式设计等相比较,响应曲面法考虑的因素很多,运算非常繁杂,建立的是复杂的多维空间曲面较接近实际情况.响应曲面法首先要寻找一个合适的近似方程来表征响应‘y’与一系列可控参数{x1,x2,…,xn}之间的真正的函数关系,通常一些未知或者非线性的函数关系可以利用二次响应模型[12]来表示:


式中,y为响应;b为回归系数;x为可控参数;ε为噪声误差.
根据以上分析,本实验有2个可控参数,故响应曲面方程形式可改为:

利用表2实验数据,进行回归分析,得到抛光压力、转速、分形维数的响应曲面方程如下:
JGS1的响应曲面方程:
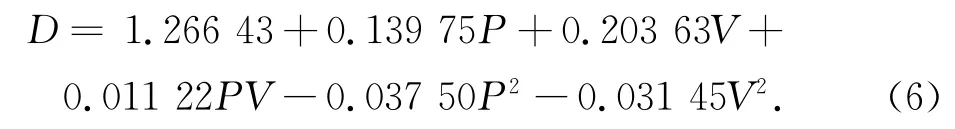
K9的响应曲面方程:
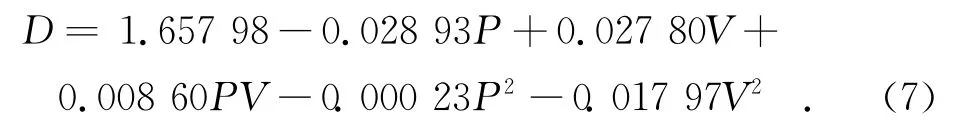
对上述响应曲面方程进行方差分析,结果如表3所示.由表3方差分析可以看出:JGS1响应曲面方程的F值大于F分布下95%置信水平下单侧临界值F0.05(5,3)=9.01且p=0.018<0.05,说明该回归方程拟合程度好,实验误差小,模型显著,能用来表征CMP抛光工艺中抛光压力、转速和分形维数之间的关系;而K9响应曲面方程的F值大于F0.05(5,3)=9.01且p=0.035<0.05,该回归方程能表征抛光参数与分形维数三者之间关系,但方程拟合程度较小,实验误差较大,显著性也不如JGS1回归方程.

表3 JGS1和K9响应曲面方程的方差分析Tab.3 Analysis of variance of JGS1and K9response surface equation
图4为抛光压力和转速对JGS1光学表面分形维数的影响.当抛光压力处于固定水平值时,分形维数随着转速的提高而逐渐增大,且增长幅度较大.当转速处于固定水平值时,分形维数随着抛光压力的提高而逐渐减小,但减小幅度较小.对抛光压力、转速进行双因子方差分析,得到分析结果,如表4所示.由表4抛光参数显著性检测结果可知,抛光压力的F=12.49>F0.05(2,4)=6.94且p=0.019<0.05,抛光压力对分形维数有显著影响;转速的F=27.59>F0.05(2,4)=6.94,p=0.005<0.01;说明转速对分形维数有极显著影响.

图4 JGS1光学玻璃CMP抛光参数对分形维数影响的响应面(a)和等高线图(b)Fig.4 Response surface(a)and contour plot indicating the effect of the CMP polishing parameters on the fractal dimension of JGS1optical glass

图5 K9光学玻璃CMP抛光参数对分形维数影响的响应面(a)和等高线图(b)Fig.5 Response surface(a)and contour plot(b)indicating the effect of the CMP polishing parameters on the fractal dimension of K9optical glass
结合图5抛光压力和转速对K9光学表面分形维数的影响与表4抛光参数显著性检测结果可得出,转速对分形维数有极显著影响,当抛光压力一定时,分形维数随着转速增加而逐渐减小,减小幅度较大;抛光压力对分形维数有显著影响,且当转速一定时,分形维数随着抛光压力的增加而逐渐减小,但减小幅度较小.
根据上述分析,在CMP加工中,抛光压力与转速对JGS1、K9光学表面分形维数有显著影响,但转速的显著性要远大于抛光压力.抛光压力的提高使JGS1、K9光学表面分形维数逐渐减小,减少幅度较小;转速的提高使JGS1光学表面分形维数逐渐增大,K9光学表面分形维数逐渐减小,且幅度较大.抛光参数对JGS1光学表面分形维数的显著性影响都要略大于K9光学表面的分形维数.
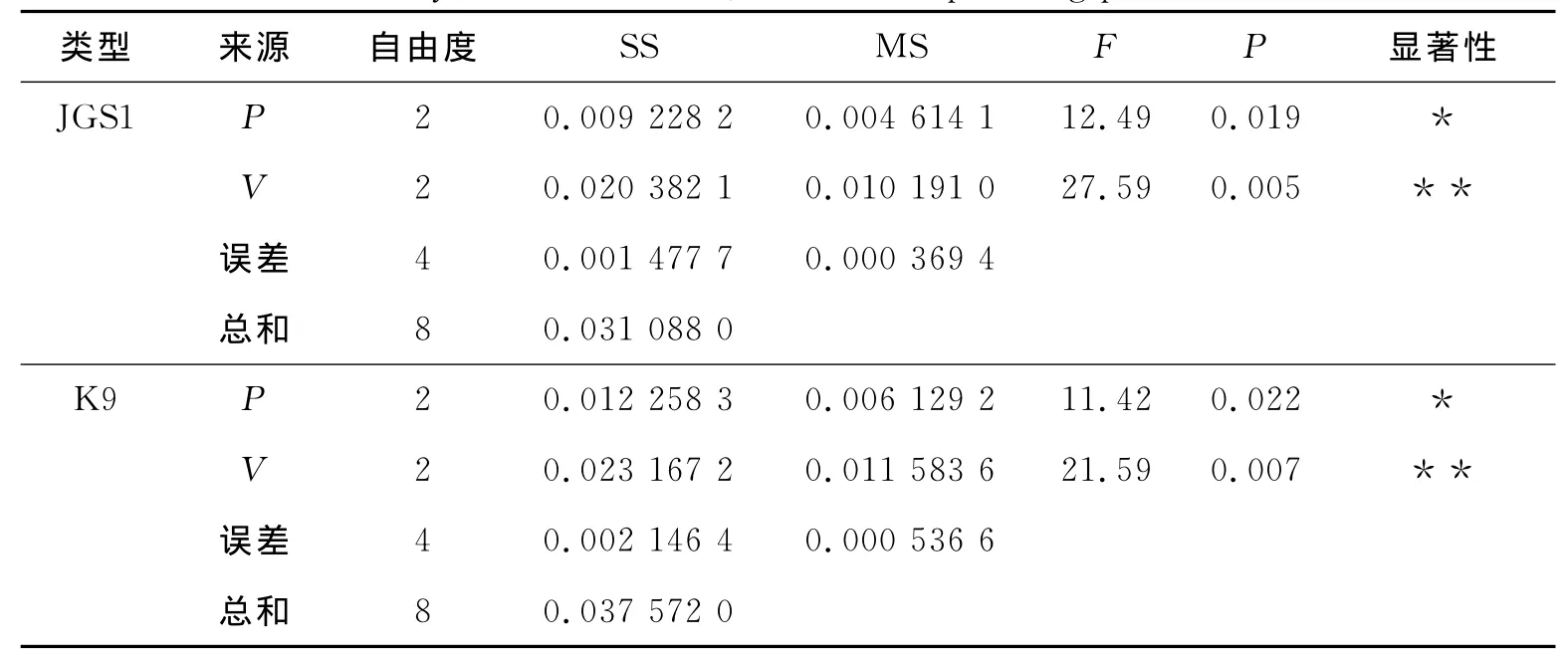
表4 JGS1和K9抛光参数P、V的方差分析Tab.4 Analysis of variance of JGS1and K9polishing parameters P,V
4 结 论
本文采用分形几何理论对JGS1、K9光学玻璃表面质量的评价方法进行研究和探讨,并通过CMP实验分析了JGS1、K9光学玻璃表面的分形特征以及CMP抛光参数、分形维数、PV值之间关系,得到以下结论:
1)光学元件表面具有分形特性,分形维数具有尺度不变性的特征,但一定程度上受采样点数的影响.
2)PV值与分形维数存在一定的近似线性关系,可认为当PV值小且分形维数大的,光学元件表面质量较高.
3)CMP实验中,拟合出的JGS1、K9光学玻璃表面响应曲面回归模型方程适合用于表征分形维数与抛光压力、转速之间的关系,比较接近实际情况;抛光压力、转速对分形维数的值都有显著影响,但转速的影响要大得多.
4)基于抛光参数、分形维数、PV值之间关系,在今后实际加工中,应优先控制转速,以取得较高的光学元件表面分形维数和较低的PV值,获得较好的光学元件表面质量.
[1]戴斌飞.面型精度评价方法研究[D].苏州:苏州大学,2005.
[2]Sayles R S,Thomas T R.Surface topography as a nonstationary random process[J].Nature,1978,271:431-434.
[3]王贵林,李圣怡,戴一帆.光学表面的分形特点与模拟表征算法[J].国防科技大学学报,2003,25(4):72-75.
[4]朱华,姬翠翠.分形理论及其应用[M].北京:科学出版社,2011.
[5]李小兵,刘莹.表面形貌分形表征方法的比较[J].南昌大学学报:理科版,2006,30(1):84-86.
[6]葛世荣,朱华.摩擦学的分形[M].北京:机械工业出版社,2005.
[7]王贵林,戴一帆,郑子文.光学表面的分形结构和表征算法[J].计量学报,2004,25(2):97-99.
[8]耿雷,刘春生,钟华燕,等.电火花线切割加工表面形貌分形特征[J].黑龙江科技学院学报,2008,18(2):114-117.
[9]高佳宏,王琳.电解机械复合抛光表面的分形特性研究[J].煤矿机械,2007,28(4):128-129.
[10]杨大勇,刘莹.两种磨削表面形貌的分形表征[J].南昌大学学报:工科版,2007,29(3):243-245.
[11]张烘州,明伟伟,安庆龙,等.响应曲面法在表面粗糙度预测模型及参数优化中的应用[J].上海交通大学学报,2010,44(4):447-451.
[12]Montgomery D C.Design and analysis of experiments[M].New York:Wiley,2001.

