北斗系统简约历书的初步设计分析

崔先强，刘 青，贾小林

（1.中南大学 地球科学与信息物理学院，长沙 410083；2.地理信息工程国家重点实验室，西安 710054；3.西安测绘研究所，西安 710054）

1 引言

在全球卫星导航系统（global navigation satellite system，GNSS）中，怎样快速地捕获卫星信号、选择几何精度因子最佳的卫星组合进行导航定位，并缩短启动导航定位的时间，一直是GNSS用户所关注的热点问题。卫星导航电文提供的历书参数信息在接收机快速地捕获卫星信号和最佳选星的过程中起着十分重要的作用。在实际的导航定位启动过程中，如果没有历书以及相关的辅助设施来提供卫星的概略位置，那么接收机只能进行 “满天搜索”，这将会大大增加接收机搜索导航卫星的时间和增大误搜率（可能搜索到其它卫星导航系统的信号），这也将会对接收机的信号通道数提出更高的要求。GNSS系统历书的主要作用是为用户提供概略的卫星位置，其主要用途表现在4个方面［1］：（1）有目的地搜索导航卫星信号；（2）找到任意卫星的概略多普勒频移，辅助频域搜索；（3）精密测量用户对某地某时的卫星可见性进行预报；（4）用于计算卫星的近似位置。

导航卫星的历书是精度较低的卫星星历，是导航电文所提供的基本数据，其对用户的重要性却不容忽视［2］。在2004年发布的全球定位系统（global positioning system，GPS）信号接口控制（interface control document，ICD）文档中，介绍了两种历书参数，即中等精度的历书（midi almanac）和简约历书（reduced almanac）［3］。其中前者与2000年发布GPS ICD文档［4］中介绍的历书参数内容相同，只是表示的位数减少了；而简约历书不仅参数位数减少，而且参数构成更加简单。在我国北斗卫星导航系统（BeiDou navigation satellite system，BDS）建设过程中，国内不少学者都对GPS的星历与中等历书参数及其用户算法进行了研究分析，据此设计出BDS的星历与中等历书参数及其用户算法，并以投入使用。对星历的研究主要表现在三个方面：首先，依据GPS星历用户算法导出了BDS中中圆地球轨道（medium earth orbits；MEO）和倾斜地球同步轨道（inclined geosynchronous orbits，IGSO）星历参数的生成算法［5-6］；其次，针对 BDS中地球静止轨道（geostationary earth orbits，GEO）卫星轨道倾角接近于零的情况提出了相应的解决措施［7-8］；最后，分析了一些影响星历参数拟合精度和效率的因素［9-10］。而历书的研究成果主要是建立BDS历书参数的生成算法［1，11］和针对参数拟合过程中存在的一些问题提出了相应的解决措施［12-13］。目前，所建立的星历与历书参数及其拟合算法已成功的用于我国BDS的运行。

简约历书是在2004年公布的GPS ICD文档中给出的，目前除了文献 ［2］及文献 ［14］对其参数及其用户算法进行分析之外，还未见相关的文献报导。为此，本文将对GPS简约历书与中等历书进行简要地比较分析，并尝试将其应用于我国的BDS并设置相应的常量参数，为我国BDS的简约历书参数及其算法设计提供参考。

2 GPS简约历书及其与中等历书的比较

GPS的简约历书参数包括4个，即历书参考时刻toa、长半轴与参考值之差δA、升交点赤经Ω0和参考时刻的纬度幅角Φ0（Φ0＝M0＋ω），其中需要估计参数为后三个，相应的长半轴参考值为Aref＝26 559 710。相对于中等历书而言，缺省参数的值分别为：e＝0、i＝55°和＝－2.6×10－9半周/秒，相应的用户算法计算步骤（与文献 ［2］类似）为：（1）改正长半轴A＝Aref＋δA；（2）计算卫星运行的平均角速度（3）计算时刻与参考时刻之差tk＝t－toa；（4）获取计算时刻的纬度幅角Φk＝Φ0＋ntk；（5）获取计算时刻的升交点经度（6）计算卫星在地固系中的坐标为

显然，简约历书的用户算法中并没有涉及到常量参数e，也就是说e的取值变化并不会影响简约历书的精度。相对于中等历书用户算法而言，简约历书的用户算法明显更加简洁，用户接收机在使用简约历书参数计算卫星位置所占用的内存和时间都将会减少。

与中等历书参数相比较，可以发现（见表1）：（1）相同的参数，简约历书所占的位数要少，且其精度也更低，如Ω0；（2）简约历书在卫星轨道长半轴的表示形式上有所变化，即选用了长半轴与参考值之差，这与GPS 18参数［15］的表示形式时一致的；（3）简约历书将近地点幅角ω和参考时刻的平近点角M0归化为了一个参数Φ0；（4）将参数e、i和直接以常量的形式给出，不需要在导航电文中进行发播，可以减小卫星的内存负荷。

表1 GPS 简约历书与中等历书对照比较表

3 BDS简约历书参数的初步设计与生成算法

相对于美国的GPS而言，我国BDS的显著特点是星座由GEO、IGSO和MEO三类卫星共同组成，由于GEO和IGSO卫星轨道特性与MEO卫星并不相同，尤其是GEO卫星轨道面倾角接近于零，导致了GEO卫星的广播星历用户算法与IGSO和MEO不同。对于BDS历书参数的生成算法，在不旋转轨道面的条件下通过实际计算可以发现，GEO的轨道面倾角接近于零并不会导致历书参数拟合发散，而且其拟合精度损失能够满足用户的实际需求，具体的计算结果见下一节算例。

为了使我国BDS能够更好地与美国的GPS兼容，初步设计与GPS简约历书相类似的参数，即包括历书参考时刻toa、长半轴与参考值之差δA、升交点赤经Ω0和参考时刻的纬度幅角Φ0（Φ0＝M0＋ω），只是根据我国BDS的特殊性，需同时设置GEO、IGSO和MEO卫星的轨道长半轴参考值，且MEO卫星轨道长半轴不一定与GPS相同。与BDS的星历参数生成算法相同的是，简约历书也同样涉及到作为常量的轨道面倾角不能直接赋值为零，否则将会导致GEO卫星简约历书生成算法发散，从而无法获得相应的简约历书参数。因此，为了保证简约历书参数拟合算法的收敛性，将GEO卫星轨道面倾角直接赋值为1°，而MEO和IGSO卫星轨道面倾角与 《北斗卫星导航系统空间信号接口控制文件》［16］里的说明相同，即取为55°。3类卫星的偏心率相同，都设为0。对于Aref和，则根据BDS的精密轨道来拟合中等历书参数，并取平均值来获得。以GEO卫星的长半轴参考值为例进行说明：首先使用一周的精密卫星轨道分别拟合出每个卫星的中等历书参数，然后取五个卫星的长半轴平均值作为GEO卫星的参考值。IGSO、MEO卫星的长半轴参考值以及三类卫星的升交点赤经的变化率采用同样的方法即可获得，所选用的轨道与算例相同。下面将直接给出相应的设定值，如表2所示。

表2 BDS简约历书常量参数取值

对于简约历书参数的生成算法，与广播星历和历书的生成算法是相同的，不同的则是卫星位置对相应参数的偏导数，这里将只给出依据前面简约历书的用户算法推导出的偏导数表达式，即

4 计算与比较

本算例所用数据为BDS卫星的精密轨道，采样间隔为5min，所取时间段为2013－10－01—07，其中03号星在2013－10－07—09时有3d机动，缺少7d的轨道，则选择了2013－09－30—10－06的轨道。我国BDS在轨卫星为14颗，由于提供的精密轨道中MEO 13－14号星没有连续的7d轨道，因此这里只选用了12颗卫星进行试算，它们分别为：1～5号是GEO星，6～10号是IGSO星，11～12号是MEO星。由于同类卫星的计算结果类似，这里将只给出1、6和11号星的拟合残差曲线图。曲线图的横坐标以历元来表示，即第一历元对应于拟合弧段的初始时刻，最后一个历元对应于拟合弧段的最后时刻。实际计算时，为了便于分析给定的参考值与常量参数发生变化对简约历书的影响，算例中除了使用表2中提供的数据外，将对其进行相应调整，并将调整前后的简约历书拟合误差作差进行分析，调整后的参数取值如表3。

表3 参考值与常量参数调整后的值

为了便于分析参考值和参数常量的变化对简约历书参数拟合精度损失的影响，接下来将分别进行讨论，具体方案及其计算如果如下。

方案一，中等历书的计算结果，如图1～图3。

方案二，表2设定值的简约历书计算结果，如图4～图6。

方案三，Aref采用表3数据时与设定值的计算结果之差，如图7。

方案四，i采用表3数据与设定值的计算结果之差，如图8～图10。

图1 01号GEO卫星中等历书拟合误差

图2 061号IGSO卫星中等历书拟合误差

图3 11号MEO卫星中等历书拟合误差

图4 01号GEO卫星简约历书拟合误差

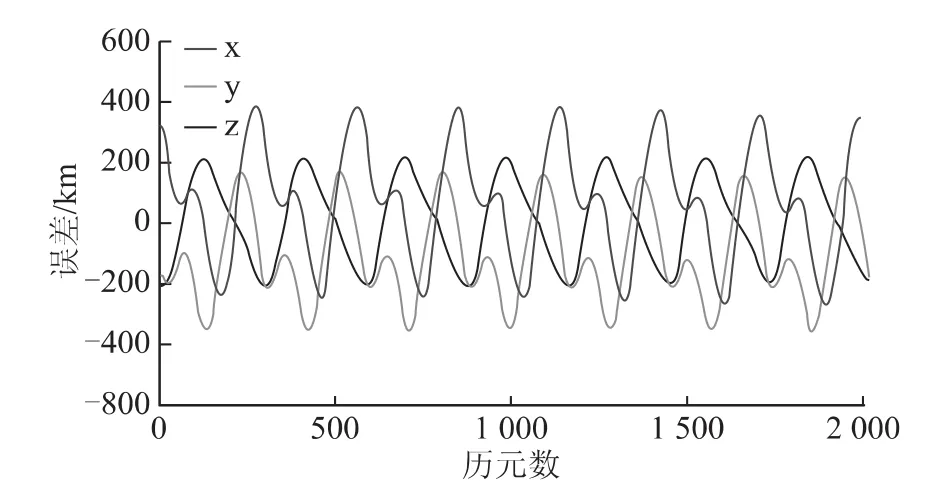
图5 06号IGSO卫星简约历书拟合误差

图6 11号MEO卫星简约历书拟合误差

图7 Aref变化前后拟合误差之差（所有卫星结果相同）

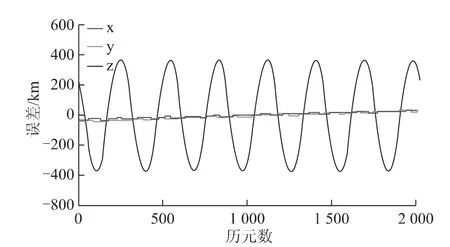
图8 01号GEO卫星i变化前后拟合误差之差

图9 06号IGSO卫星i变化前后拟合误差之差

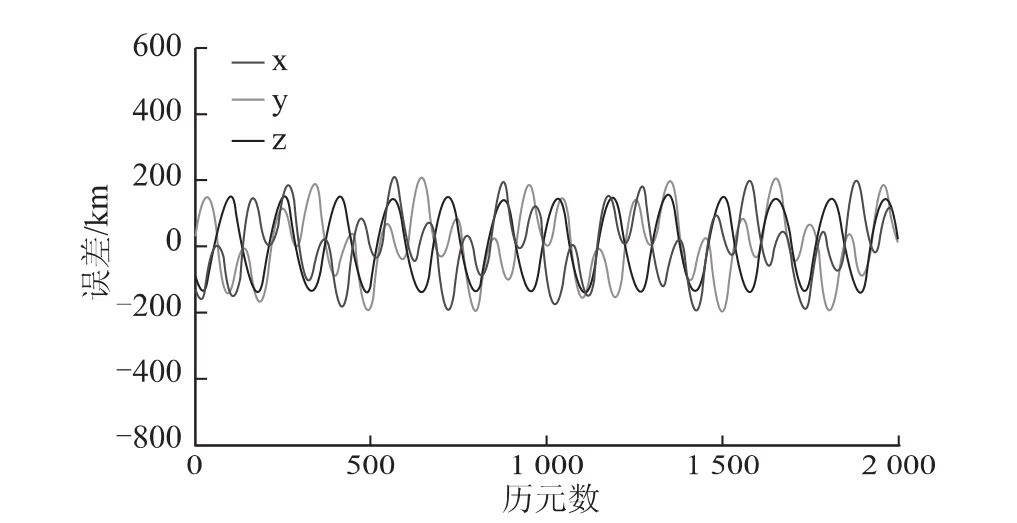
图10 11号MEO卫星i变化前后拟合误差之差

图11 01号GEO卫星变化前后拟合误差之差

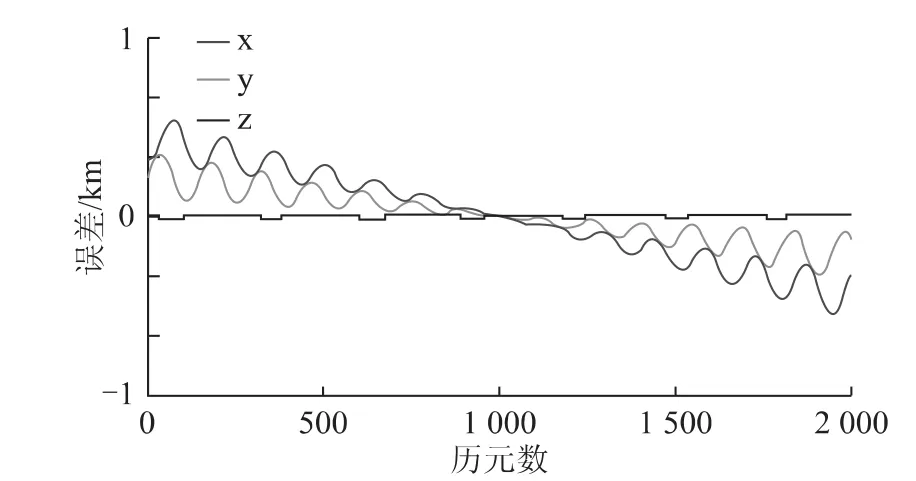
图12 06号IGSO卫星变化前后拟合误差之差

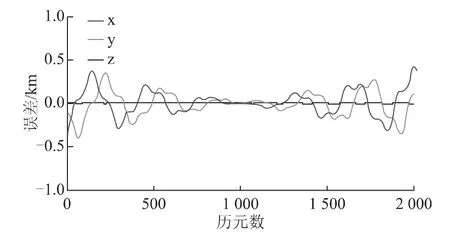
图13 11号MEO卫星变化前后拟合误差之差

由计算结果可以看出：

（1）将方案一（图1～图3）与方案二（图4～图6）结果进行对比可以发现，中等历书参数的精度要明显地优于简约历书参数，原因在于简约历书参数直接给出的3个参数i、e和的值与真实值之间存在较大的偏差。

（2）根据表2所设定的A参考值和常量参数所计算出的简约历书参数的拟合残差都在600km以内，而且MEO卫星的结果（图6）要明显地优于文献 ［2］的计算结果，原因在于文献 ［2］中的简约历书参数直接来自于广播星历，而本文则是采用最小二乘算法拟合得到，使得部分误差得到了较好的控制。

（3）从方案三的误差曲线图（图7）可以看出，选择不同的长半轴参考值所获得的简约历书参数拟合结果是相同的，即对长半轴进行调整前后的拟合残差之差为0，这说明长半轴参考值设置的精确与否并不会影响整个简约历书参数的精度。

（4）方案四的计算结果（图8～图10）显示出，较小的倾角变化将会引起简约历书的较大误差，尤其是针对GEO卫星倾角本就接近于0的情况，因此在设置简约历书的常量参数i时，必须尽可能的逼近于真实轨道。

（5）从方案五的计算结果（图11～图13）可以看出，相对于简约的拟合残差来说，的较小波动引起的简约历书拟合残差的变化并不是很大，尤其是在z方向的影响几乎接近于0，而且GEO和IGSO卫星水平方向的变化具有明显的系统性倾向。

5 结束语

本文对GPS中等历书和简约历书进行了比较分析，并基于此初步设计了我国BDS的简约历书参数及其相应参考值和常量参数，导出了卫星位置对简约历书参数的偏导数，分析了影响BDS简约历书拟合精度的一些影响因素，可得出如下结论：

（1）在简约历书的用户算法中，并没有涉及到轨道偏心率e，因此直接赋值为0即可。

（2）长半轴参考值Aref存在一定的误差并不会影响简约历书参数的精度；

（3）轨道面倾角i的微小波动可能会导致简约历书拟合残差的较大变化，尤其是实际倾角接近于零的GEO卫星，因此在设计常量参数轨道面倾角i时必须与轨道真实值一致；

［1］陈留成，胡小工，韩春好，等.导航卫星历书参数拟合算法［J］.天文学报，2008，49（3）：288－296.

［2］陈南，陈大恒，贾小林.GPS新民用导航电文简约历书的算法和性能分析［J］.测绘工程，2006，15（6）：63－66.

［3］IS－GPS－200，Revision D.Navstar GPS Space Segment/Navigation User Interface［S］.

［4］ICD－GPS－200，Revision C－004.Navstar GPS Space Segment/Navigation User Interface［S］.

［5］崔先强，焦文海，贾晓林，等.GPS广播星历参数拟合算法［J］.测绘学院学报，2004，21（4）：244－246.

［6］陈留成，韩春好，陈金平.广播星历参数拟合算法研究［J］.测绘科学，2007，32（3）：12－14、192.

［7］黄勇，胡小工，王小亚，等.中高轨卫星广播星历精度分析［J］.天文学进展，2006，24（1）：81－88.

［8］崔先强，杨元喜，吴显兵.轨道面旋转角对 GEO卫星广播星历参数拟合的影响［J］.宇航学报，2012，33（5）：590－596.

［9］崔先强，焦文海，秦显平.GPS广播星历参数拟合算法的探讨［J］.测绘科学，2006，31（1）：25－26，48.

［10］陈留成，唐波.参考系选择对 Kepler广播星历参数拟合精度的影响［J］.飞行器测控学报，2006，25（4）：19－25.

［11］崔先强，焦文海，秦显平.导航卫星的历书参数及其拟合算法［J］.测绘科学技术学报，2006，23（1）：23－25.

［12］陈留成，唐波，梁红梅.导航卫星历书参数拟合改进算法［J］.天文学进展，2008，26（1）：80－86.

［13］莫中秋，陈留成，董恩强，等.导航卫星历书拟合初值的选取与误差分析［J］.测绘科学技术学报，2008，25（2）：104－107.

［14］陈南，贾小林，崔先强.GPS民用导航电文CNAV的特点［J］.全球定位系统，2006（1）：1－6，34.

［15］崔先强，焦文海，贾晓林，等.两种 GPS广播星历参数算法的比较［J］.空间科学学报，2006，26（5）：382－387.

［16］中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件［EB/OL］.［2013－12－08］.http：//wenku.baidu.com/link？url＝PzhulclXTbE61jIdz6YkAa1B6－IlQE17LTZbngeJRMGQXiaGXhPeFcWmDNbrWd6GaI2oxmYLQx 6TZCxEWKO07Srj62N2i5EYbA2kVJmAFYm.