双卫星导航系统短基线动态定位实验与对比分析

张小红，丁乐乐，2，何 俊

（1.武汉大学 测绘学院，武汉 430079；2.天津勘察院，天津 300191）

1 引言

随着美国全球定位系统（global positioning system，GPS）现代化的实施、俄罗斯格洛纳斯卫星导航系统（global navigation satellite system，GLONASS）的完善、欧洲伽利略卫星导航系统（Galileo navigation satellite system，Galileo）及我国北斗卫星导航系统（BeiDou navigation satellite system，BDS）的建成，多系统组合导航定位将成为必然趋势。与单系统定位相比，多系统组合定位具有以下优势：1）组合系统观测到的卫星数目显著增多，卫星空间分布几何构型更好，能选择几何结构更好的卫星组进行定位，可提高定位精度和可靠性；2）能提高遮挡环境下的可视卫星数，增加了卫星导航定位的可用性；3）观测更多的卫星能增强定位的可靠性。观测到的卫星数越多，系统的抗粗差能力越强，定位的可靠性也就越高；4）多系统组合定位，也将减小对单系统的依赖。国内外已有很多学者和机构已经对多卫星导航系统组合定位进行了仿真研究或利用实测数据进行了实验，并取得了不少成果［1-3］。目前，对 GPS/GLONASS组合的研究较多，对GPS/BDS组合定位方面的研究刚起步。

BDS已于2012年底初步建成了由14颗卫星组成的区域导航系统，可实现中国及周边地区的精确导航定位。北斗系统正处于组网建设阶段，BDS卫星颗数相对较少，定位的可靠性和精度还不如GPS系统，但是GPS系统在卫星数不足的情况下（如高楼密集的城区）也不能提供连续无缝的导航定位，GPS/BDS组合定位就有可能解决这一问题。本文以GPS和BDS组合定位为研究对象，讨论组合定位的观测模型及组合定位的时空基准统一，重点比较研究单系统定位和组合定位的性能，讨论GPS组合BDS观测能给高精度用户带来的好处。

2 GPS/BDS双差观测模型

采用传统的双差模型进行相对定位。对于短基线，GPS/BDS组合相对定位的观测方程可简化为［6］

式（1）中，G和B分别代表GPS卫星和BDS卫星，ΔΔ代表双差算子，P为伪距观测值，ρ为卫星j至观测站k的几何距离，c为光速，φ是载波相位观测值，N为载波相位整周模糊度，εP、εφ分别为伪距观测噪声和载波测量噪声。对于短基线，可认为接收机钟差、卫星钟钟差、电离层延迟，对流层延迟在双差的过程中基本消除。

由于GPS和BDS信号频率不同，在组合定位中，笔者采用的双差策略是在各自卫星系统中选取参考星形成双差观测值，以保证所有的双差模糊度为整数。

3 组合定位的时空基准转换

GPS和BDS分别采用各种的时空基准，在定位解算时，需要考虑时空基准的统一。

北斗时（BeiDou navigation satellite system time，BDT）是 国 际 原 子 时 （international atomic time，TAI）从2006－01－01T00：00：00开始起算的原子时，与国际原子时保持有33s的常数差。GPS时（GPS time，GPST）与TAI保持有19s的常数差，并在 GPS标准历元1980－01－06T00：00：00与协调世界时（coordinated universal time，UTC）保持一致。因此，GPS时换算为北斗时需要减去14s。

BDS卫星星历拟合参数是以CGCS 2000中国大地坐标系为参考的，因此，BDS定位的坐标及相对定位中解算的基线向量属于CGCS2000大地坐标系。GPS定位的坐标及相对定位中解算的基线向量属于WGS－84大地坐标系。由于上述两个坐标系定义上一致，即坐标系原点、尺度、定向及定向演变的定义都是相同的，因参考框架不同而引起的相对定位结果的差异很小，可忽略不计［7］。 因 此， 在 短 基 线 解 算 时， 笔 者 忽 略CGCS2000和WGS－84坐标系统间的差异，近似认为是同一个参考框架。

4 参数估计

在动态基线解算时，参数估计采用的是扩展卡尔曼滤波模型［8-9］。通过使用扩展卡尔曼滤波，状态向量x和它的方差协方差阵P可以通过下式递推估计

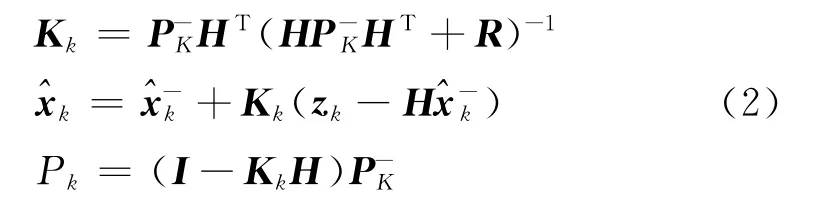
式中，zk、H、R分别表示量测向量、设计矩阵和观测误差的方差协方差阵。在扩展卡尔曼滤波中，假定系统模型为线性的，状态方程时间更新和它的方差协方差阵表示为

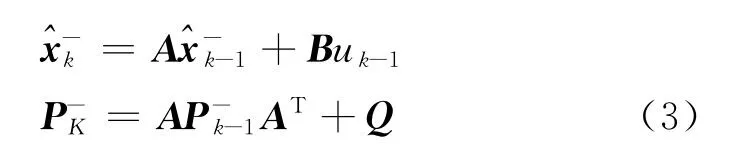
式中，A是状态转移矩阵，Q是系统噪声的方差协方差。当采用卡尔曼滤波获得载波相位模糊度的实数值及其方差协方差矩阵后，即可以采用整数最小二乘降相关分解法（least－square ambiguity decorrelation adjustment，LAMBDA）解算其整周模糊度值［10］。其中，LAMBDA方法采用整数最小二乘估计，目标函数如下

式（4）中，为模糊度实数值，为模糊度整数值，为模糊度的方差协方差矩阵。候选的整数模糊度又很多个组合，通常采用搜索的方法获得最优整数模糊度组合。模糊度固定后，就可以利用下式计算基线向量的固定解。

5 数据处理及结果分析

本文主要利用短基线实验进行结果的对比分析，其中包括静态模拟动态基线解算和实际动态基线解算。

实验一为静态模拟动态实验，是2013－04－17 UTC 06：30：06－UTC 08：02：48用和芯星通公司生产的双频双系统接收机采集的静态观测数据，采样率为1s，实验地点为武汉大学测绘学院楼顶。静态试验两测站分别命名为JT01、JT02。

实验二为动态实验，是2013－03－20进行的车载试验，接收机为Trimble NetR9。车顶前后固定两个接收机天线，数据采集时间段为UTC 06：04：56－UTC 07：36：45，车载实验时沿着一段开阔的路段行驶。动态试验两测站分别命名为DT01、DT02。

5.1 卫星星座及可见性分析

首先对比分析了卫星分布、可见卫星数以及位置精度衰减因子（position dilution of precision，PDOP）的情况。图1中给出了GPS和BDS实验一UTC 06：32：50的卫星天空视图。

图1 GPS与BDS卫星天空视图

从图1中可以看到，当时的GPS可视卫星数为8颗；BDS可视卫星数为9颗，且集中分布在的一侧，这与当前BDS工作的星座有关，因为编号为1、3、4、5的BDS卫星为地球静止轨道（geostationary earth orbits，GEO）；而编号为6、7、8、10的BDS卫星为倾斜地球同步轨道（inclined geo－synchronous orbits，IGSO）。两者组合则显著改善了单系统的几何图形结构。

图2中给出了实验一当天GPS/BDS的卫星数和PDOP值变化。从图2中可以看出，当天该站的GPS可视卫星数为6～8颗；BDS可视卫星数为9颗；GPS/BDS双系统组合可视卫星数达到15～17颗。从PDOP角度分析，BDS的位置精度因子较GPS的位置精度因子大；相比于单系统，GPS/BDS组合显著改善了卫星的空间几何分布，组合后的PDOP值明显优于单系统的PDOP。对于高楼林立的城区，在单系统可视卫星数不足时，组合能够增加可视卫星数，进而改善定位的几何精度因子。

5.2 静态模拟动态基线解算及结果分析

图3为实验一中JT01－JT02基线分别采用单系统和GPS/BDS双系统组合动态基线解算在E、N、U三个分量的定位结果。

从图3中可以看出，GPS/BDS组合动态基线解算精度在N、E、U方向上均优于单系统基线解算的精度；各方向上解算的最大误差E方向在2cm之内；N方向在3cm之内；U方向在6cm之内。对各个方向基线向量在不同区间的值的个数进行统计，得到统计直方图，如图4所示。

图2 单天卫星数与PDOP时序图

图3 短基线N、E、U方向分量

从图4可以看出，基线分量的值分布在均值的两侧并且基本符合正态分布。从统计直方图可以看出，GPS/BDS的误差分布最为集中，GPS、BDS单系统的分布相差不大。采用数理统计的方法可以得到各种单系统与双系统组合情形下，不同方向上的均方根误差（root mean square，RMS）如表1所示。

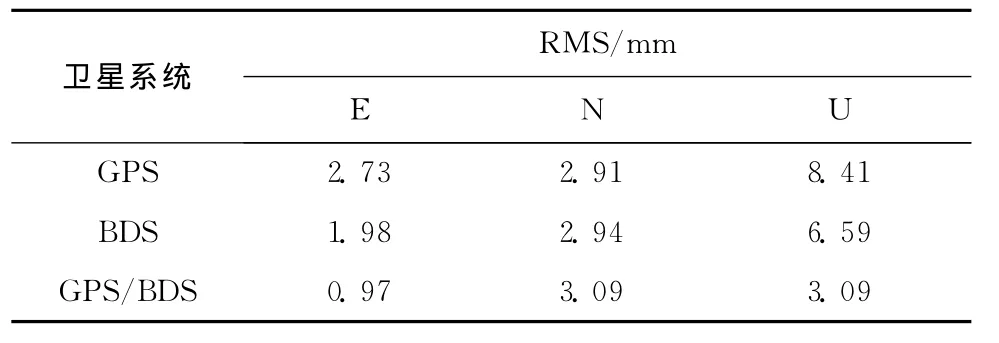
表1 GPS/BDS组合基线解算精度统计表

从表1中可以看出，在E、U两个方向上，GPS/BDS组合静态模拟动态基线解算的RMS均小于单系统对应的RMS小，N方向三者精度相当。

图4 N、E、U分量的统计直方图

5.3 单差残差分析

为了进一步分析不同系统的差异及组合定位的优势，下面将对单差观测值的残差进行分析。双差观测值的残差随着高度角变化而变化，但双差形成过程中，需要选择参考星，这使得双差残差无法真实反映参考星随高度角变化时的统计性质。站间单差残差可以反应观测值的精度，同时站间单差残差可作为验后加权的依据。下面对GPS和BDS的单差残差进行分析。

GPS以PRN14号卫星为例，图5给出了该卫星的单差残差序列，其中解算过程的截止高度角为5°。从图5中可见，卫星高度角越小其观测值的单差残差越大。相比于L1载波，L2载波的单差残差在低高度角时噪声更大，L1载波的单差残差则变化较为平稳。卫星高度角低于10°时。载波和伪距残差都会较大。

图6给出了BDS10号卫星观测值B1、B2、P1、P2单差残差序列变化图。从图6中可见，当卫星高度角大于20°时，卫星单差残差变化不大，当卫星高度角小于10°时，卫星的单差残差迅速增大。

对比图5和图6中卫星高度角变化序列可知，每颗GPS卫星一天内的可观测时间段要比BDS卫星短；同步卫星GEO为全天候可见；IGSO为倾斜地球同步轨道卫星，连续可见时间较GPS长很多。从GPS和BDS单差残差统计分析可知，单差残差随着高度角变化很明显，尤其是卫星高度角较低时，单差残差会比较大。此外，BDS的载波和伪距观测噪声要比GPS的观测噪声大。建立适合GPS/BDS组合基线解算的随机模型可进一步提高组合基线解算的精度［11-12］。同时，组合后的卫星数较多，可适当提高截止卫星高度角来提高基线解算的精度。

图5 GPS14号卫星单差残差

图6 BDS10号卫星单差残差

5.4 GPS/BDS组合动态相对定位结果及统计分析

下面给出实验二中车载动态相对定位的实验结果，由于当时BDS不够稳定，单BDS动态数据解算结果中存在少数较大的粗差，为了方便与GPS的定位结果和组合结果进行比较，结果中剔除了单BDS不能固定模糊的部分历元的定位结果。在车载实验中，动态基线解算的真值无法确定，车上两天线间的距离保持不变，可以作为处理结果的外部检核。图7给出了逐历元动态基线长度的结果。

图7中的基线解算给出了将近1h的动态基线测量结果。由定位结果可知，GPS/BDS组合短基线解算较单系统基线解算精度有所提高。从图7可以看出，基线解算长度集中在0.66～0.68m之间，GPS/BDS组合解算的基线长度统计最为集中。经计算，解算的基线长度精度BDS为6.8mm、GPS为5.3mm、GPS/BDS组合解算为4.5mm。

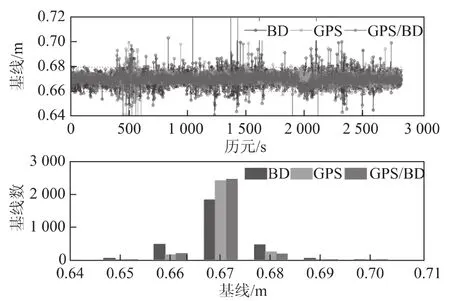
图7 动态基线解算结果

6 结论与展望

上述两个实际的观测实验结果表明：GPS/BDS组合动态基线解算精度和可靠性较单系统有明显改善。从误差源考虑，BDS与GPS观测值精度相当，但BDS的GEO卫星在武汉地区的卫星高度角基本上都在30°以上，从而不会出现低高度角卫星的观测值由于电离层和对流层延迟误差较大的现象，这对中纬度地区的定位用户来说具有显著优势。但是由于北斗系统GEO卫星基本不动，IGSO卫星运动范围也较小，一些测站可能受到某个方向上信号的遮挡，可能会出现接收不到卫星信号而长时间无法定位的问题，但随着BDS中圆地球轨道（medium earth orbits；MEO）卫星的增加，这一局面将得到改善。

随着BDS性能的逐步提升，BDS导航定位完全可以做好甚至优于GPS系统，今后的研究重点将聚焦于中长距离的BDS高精度定位实验和BDS三频模糊度快速解算等方面。

［1］高星伟，李毓麟，葛茂荣.GPS/GLONASS相位差分的数据处理方法［J］.测绘科学，2004，29（2）：22－24.

［2］郝明，王庆良.基于 GPS单频接收机的精密单点定位研究［J］.测绘科学，2010，35（2）：123－124.

［3］张小红，郭斐，李星星，等.GPS/GLONASS组合精密单点定位研究［J］.武汉大学学报：信息科学版，2010，35（1）：9－12.

［4］谭述森.卫星导航定位工程［M］.北京：国防工业出版社，2010.

［5］万祥，张孟阳.北斗高动态双频相对定位技术［J］.飞行测控学报，2010，29（3）：68－73.

［6］李征航，黄劲松.GPS测量与数据处理［M］.武汉：武汉大学出版社，2005.

［7］魏子卿.2000中国大地坐标系及其与 WGS84的比较［J］.大地测量与地球动力学，2008，28（5）：1－5.

［8］KIM D，LANGLEY R B.Kalman－filter Based GPS Ambiguity Resolution for Real－time Long－baseline Kinematic Applications［EB/OL］.（2000－07－05）［2013－12－26］.http：//gauss.gge.unb.ca/papers.pdf/cei.poland.00.pdf.

［9］YANG Yuan－xi，HE Hai－bo，XU Guo－chang.Adaptively Robust Filtering for Kinematic Geodetic Positioning［J］.Journal of Geodesy，2001，75（2－3）：109－116.

［10］TEUNISSEN P J G.Least－squares Estimation of the Integer GPS Ambiguitiess［EB/OL］.［2013－12－26］.http：//pages.citg.tudelft.nl/fileadmin/Faculteit/CiTG/Over＿de＿faculteit/Afdelingen/Afdeling＿Geoscience＿and＿Remote＿Sensing/pubs/PT＿BEIJING93.PDF.

［11］WANG Jin－ling.Stochastic Modeling for RTK GPS/GLONASS Positioning［J］.Navigation，1999，46（4）：297－305.

［12］张小红，丁乐乐.北斗二代观测值质量分析及随机模型精化［J］.武汉大学学报：信息科学版，2013，38（7）：832－836.