基于北斗系统测速方法的对比分析

李志斌，蔡成林，王利杰，邓克群，韦照川

（桂林电子科技大学，桂林 541004）

1 引言

全球卫星导航系统（global navigation satellite system，GNSS）用户测速方法可归结为如下三种：位置差分测速法、载波相位差分测速法以及原始多普勒观测值测速法［1］，分析结果指出：位置差分测速法精度可达到分米级，而多普勒测速精度可达到毫米级［2-3］。文献 ［4－5］指出这三种测速方法均具有各自的优势，不能一味地认为某一种测速方法最好，位置差分测速法和载波相位差分测速法的测速精度受载体运动状态的影响较大，相对而言，原始多普勒测速法主要取决于多普勒观测值的精度，基本不受载体运动状态的影响，所以该方法备受业界推荐。

尽管全球定位系统（global positioning system，GPS）测速方法取得了许多可喜的研究结果和工程应用，但是我国的北斗卫星导航系统（BeiDou navigation satellite system，BDS）采用地球静止轨道（geostationary earth orbits，GEO）卫星、倾斜地球 同 步 轨 道 （inclined geo－synchronous orbits，IGSO）卫星及中圆地球轨道（medium earth orbits；MEO）卫星的多类导航卫星的星座结构，其中GEO与MEO/IGSO卫星位置和速度解算存在显著差异，致使BDS整体测速算法与GPS测速算法具有一定的差别。当前，BDS已正式运行服务，深入研究BDS测速精度对提供BDS用户测速服务性能具有现实意义。本文通过对多普勒测速法和位置差分测速法的研究，从原理上分析了BDS系统中三种卫星位置求解的异同点，采用实测数据分析了两种测速方法的优劣性。

2 BDS测速原理

2.1 位置差分测速法

利用起始历元t－Δt和停止历元t＋Δt的位置向量S1和S2，求出历元t的载体速度3

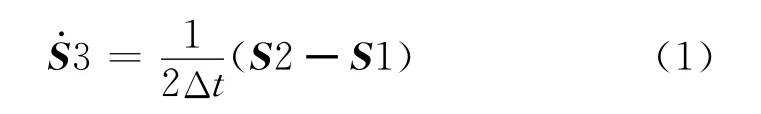
式（1）中，Δt为采样间隔，但是需要注意的是这里计算出来的3为2Δt时段内的平均速度，当Δt趋近于0时，3即是t时刻的瞬时速度［6］。

2.2 多普勒测速法

当卫星和用户之间存在相对运动时会引起多普勒频移。假设卫星和用户之间的相对速度为，用户至卫星视线方向的单位矢量为a，用户位置u＝（xu，yu，zu）已经解算出来，并且其离开线性化点的偏移值 （Δxu，Δyu，Δzu）是在用户所要求的范围内的。其相对运动引起的多普勒频移可表示为

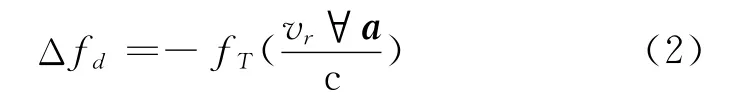
该方法不仅可以计算出接收机的速度＝，），还可以确定接收机的时钟漂移。

下面具体阐述多普勒测速原理。对于第j颗卫星来说，接收机收到的频率用多普勒方程近似表示为

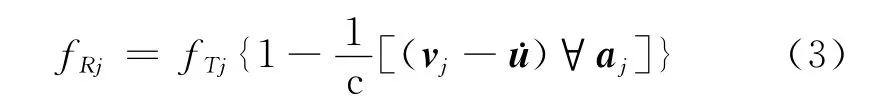
式中，fRj为接收机接收到的第j颗卫星的频率，fTj为第j颗卫星实际的发射频率，vj＝ （vxj，vyj，vzj）为第j颗卫星的速度矢量，为接收机的速度矢量，aj＝ （axj，ayj，azj）为沿从接收机指向第j颗卫星的直线方向的单位矢量。

对于第j颗卫星来说，接收机接收信号频率的测量估计值记为fj，但是这些测量值是有误差的，其与fRj的值相差一个频偏偏移。然而这个偏移与用户时钟相对于BDS时的漂移存在如下关系式

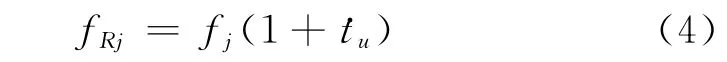
式（3）中的fTj由导航电文所导出的频率校正值获得，然而一般将这个校正值忽略不计，即fTj由卫星标称发射频率f0代替，因此fj－fTj可直接用多普勒频移Δfd近似表示。将式（3）点积用矢量分量展开，令

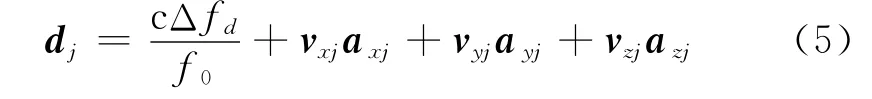
将式（5）和式（4）代入式（3）整理化简得

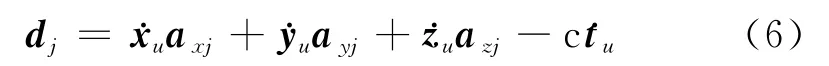
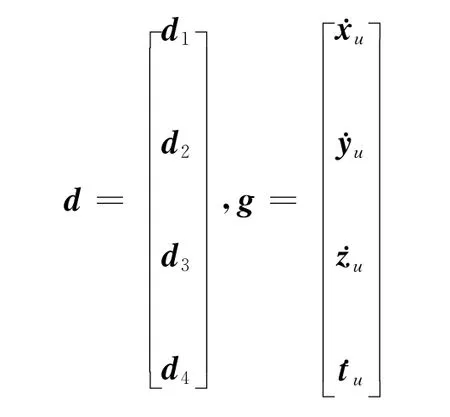
则用矩阵求解方程为

如果多于4颗卫星，可用最小二乘法来计算［7］，矩阵解算方程表示为

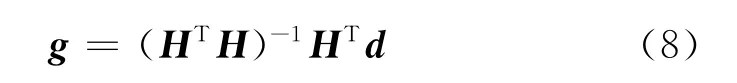
2.3 BDS卫星速度求解

BDS采用三种导航卫星（MEO、IGSO及GEO）的星座结构［8］及2000中国大地坐标系（CGCS2000），用户可以根据接收到的星历参数来计算卫星在CGCS2000坐标系下的坐标。

CGCS2000坐标系的基本常数为

长半轴：a＝6 378 137.0m

地球引力常数

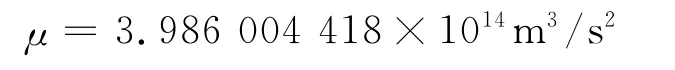
地球自转角速度

其中MEO/IGSO与GEO的卫星位置计算稍有不同，下面将主要区别加以阐述。

参数介绍如下：toe为参考历元时刻；为观测历元时刻；Ω0为按参考时间计算的升交点赤经；为升交点赤经变化率；ik为改正后的轨道倾角；（xk，yk）为卫星在轨道平面内坐标。

（1）求解MEO/IGSO卫星位置

计算历元升交点的赤经（地固系）

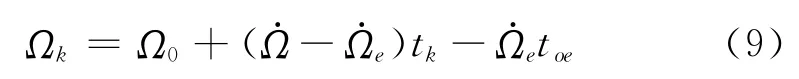
记 （Xk，Yk，Zk）为卫星在CGCS2000坐标系下的坐标，则

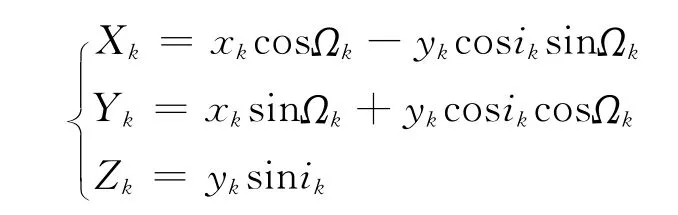
（2）求解GEO卫星位置

计算历元升交点的赤经（惯性系）：

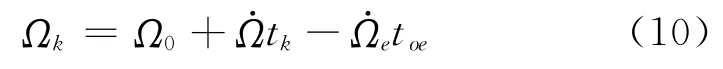
记 （XGK，YGK，ZGK）为其在自定义坐标系中的坐标，（Xk，Yk，Zk）为CGCS2000 坐 标 系 中 的 坐标，则

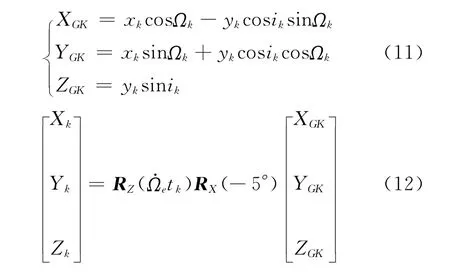
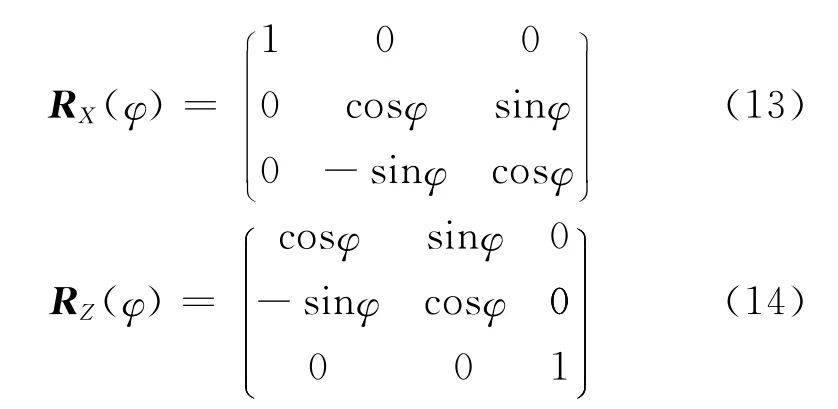
其中，RZ（tk），RX（－5°）是 坐 标 转 换 矩 阵RX（φ）和RZ（φ）在φ取相应值时候的矩阵，旋转矩阵公式为

求卫星速度即是对卫星位置求导，这里对卫星在CGCS2000坐标系中的位置坐标 （Xk，Yk，Zk）求导即可。

这里只将GEO与MEO/IGSO卫星位置计算过程中主要区别加以阐述，具体计算过程请查阅相关文献。

3 实例分析

此次测速实验所用接收机为和芯星通生产的UR240－CORS－IIBDS/GPS双系统4频OEM接收机。该接收机采用了抗多路径算法及高性能射频前端设计，能提供高质量的原始观测量输出。该接收机同时可以输出其速度参量，为测速实验提供依据。

实例分析分别从静态和动态做了三组不同的实验，其中实例1为静态测量，实例2及3为动态测量，实验日期为2013－05—06。每组实验得到三种不同的速度，其中一种为接收机自身输出，另外两种为测速算法所得，分别采用位置差分测速法和多普勒测速法。综合对比分析这三组实验以及每组实验的三种速度得到相关结论。

3.1 测速实例1

静止状态下，接收机的速度为零，可以把静止状态看作接收机做速度为零的匀速运动。选择天气晴朗的时候，于2013－05－06，接收数据大约10min，采样频率为2Hz（周期为0.5s），经过误差剔除以及时间同步筛选后历元数为500。整理接收机输出数据，分别用多普勒测速法和位置差分测速法计算接收机的速度，因为此时知道接收机的速度真值，所以很容易的对两种方法做出对比分析，下表1为该采样频率下速度误差标准差的统计情况。

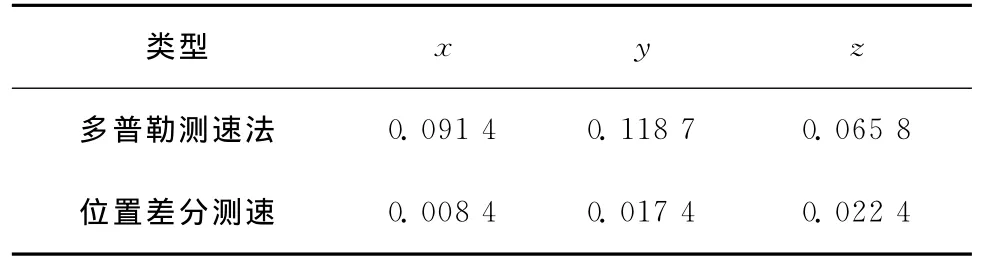
表1 速度误差标准差数据统计表/（m·s－1）

由于接收机的速度为零，从表1的统计结果可以看出，位置差分测速法的精度明显要优于多普勒测速法精度。因为位置差分测速法反映的为载体的平均速度，只有当Δt趋近于零时，才是载体的瞬时速度。所以通过该实验可以大胆推测，载体做理想匀速运动时，只要采样率满足要求（21Hz甚至以下），那么位置差分测速法精度要优于多普勒测速法精度。

3.2 测速实例2

动态测量实验选择地点为桂林绕城高速，时间为2013－05－04，在天气晴朗的时候将接收机放在汽车上面，然后以大约60km/h（约为16.67m/s）的速度行驶约0.5h，采样频率为2Hz，经过误差剔除以及时间同步筛选后历元数为450。提取该接收机输出的数据，分别用多普勒测速法和位置差分测速法算得载体的速度，再经过去噪、平滑得出最终结果。由于汽车的运行速度没有真值，因此无法确定解算的速度的准确性，而多普勒测速是经过很多专家学者验证过的比较精确的测速方法，所以这里暂时先采用多普勒测速作为测速基准［8］，来对比分析这三种速度。图1、图2分别为多普勒测速速度、接收机输出速度以及位置差分测速速度的比对以及其互差结果。

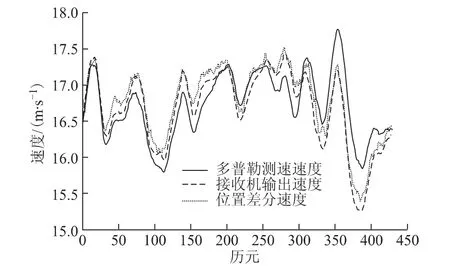
图1 三种速度图形

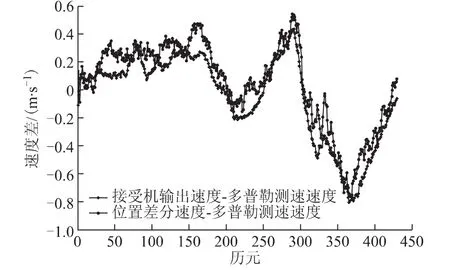
图2 两种速度差图形

由图1可以看出，位置差分测速法虽然和接收机输出速度大致相近，但是其只能比较好的显示汽车速度匀速的情况。而多普勒速度在汽车速度跳变的时候是比较稳定的。但是由图2可以看出，多普勒测速结果与接收机输出速度的差值还是要明显大于其与位置差分法测速结果的差值。而且速度差值方面，后者明显要比前者稳定。

根据这次实验的结果分析，位置差分测速法要稍微优于多普勒测速法。但是经过很多GPS以及BDS导航方面专家和学者的测试验证，对于实际生活中的载体运动，多普勒测速是明显优于位置差分测速的。针对这种情况，经过仔细的思考，一方面发现由于广西大部分地区为典型的喀斯特地貌，而桂林更是很难找到一段两边没有山的宽敞大路，另一方面就是在桂林绕城高速上行驶接收数据的时候，还穿过了很多桥洞，这些因素都会对BDS数据的接收造成一定方面的影响和干扰，从而影响实验结果。而这一次的数据采集，只考虑到天气对接收数据的影响，并没有考虑到这些小山峰和高速建筑物对接收数据的干扰，所以得出的实验结果与理想结果有偏差。

3.3 测速实例3

基于上述情况，为了减弱甚至消除山峰和高速建筑物这方面的干扰，于2013－06－21进行了第二次动态测量。这次选择桂林机场高速，汽车以70km/h（约为19.44m/s）的速度行驶约0.5h，采样频率依然为2Hz，速度基准仍然选择多普勒测速法，经过误差剔除以及时间同步筛选后历元数为1 500。经过整理、去噪、平滑后，得出三种速度。其结果如图3、图4所示：

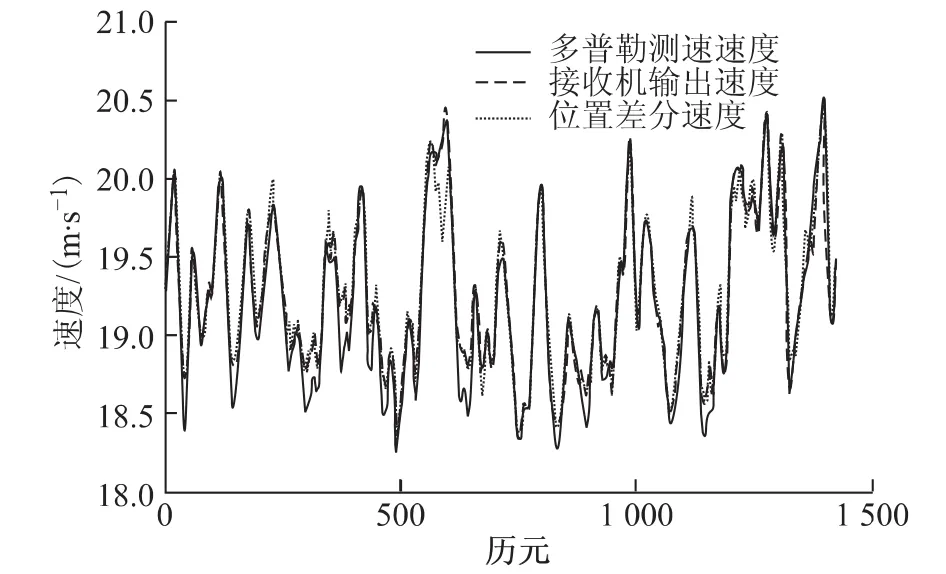
图3 三种速度图形

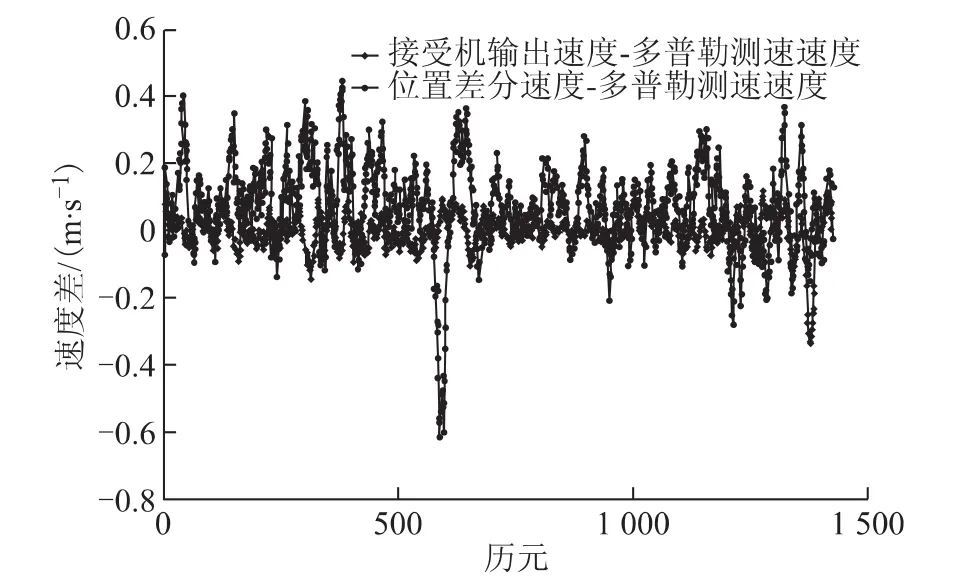
图4 两种速度差图形

由图3、图4可以明显的看出来，这次由于对接收数据干扰工作考虑的比较充分，数据的连续性以及图形的稳定性要明显优于第一次，可用历元数也大大多于第一次测速（第一次可用历元为450，这次为1 500）。由图3可知，多普勒测速和接收机输出速度图形基本吻合一致，能实时、稳定的反映汽车速度的变化，尤其体现在变速过程中。而从位置差分测速法的图形来看，其在加速或者减速的过程中对速度的计算还差不多，但是在速度变化相对比较快的区域，比如速度突然由增加趋势变化为下降趋势或者由下降趋势转化为上升趋势时，位置差分测速法对速度的估计都呈现不稳定的状态，也就是不能实时反映汽车速度的变化。由图4可以看出，位置差分测速法与多普勒测速法的差值变化波动较大，范围在0.6m/s以内，尤其是在速度出现拐点的时候（比如第600历元左右），其差值更大。而多普勒测速与接收机输出速度的差值还是比较稳定的，基本维持在0.2 m/s以内，（但是在第1 300历元到第1 400历元之间还是出现一个较大的波动，原因有可能为该时刻汽车由于颠簸而导致接收机接收数据出现跳动造成）。总体来说这两种速度都可以实时反映汽车速度的变化，并且它们的精度差不多。

表2给出了三种速度和两种速度差的统计情况。

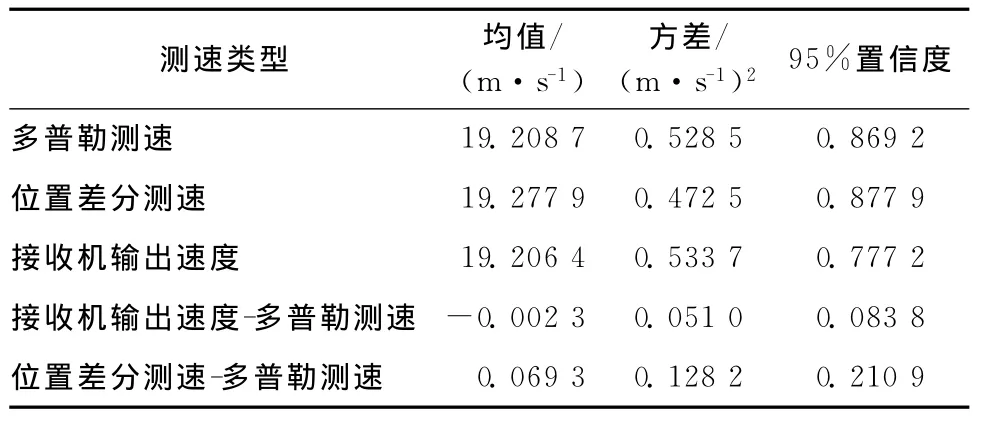
表2 各速度与速度差数据统计表

由表2可以看出来，三种测速方法得到的速度的均值相差在厘米级，而由于测速过程中，汽车速度被人为大致控制在70km/h（即19.44m/s）。因此，可以从下面两个方面来分析该统计表。

（1）从整个过程来考虑，汽车可以近似看作是匀速运动的，而位置差分测速在计算理想匀速运动载体速度的时候是优于多普勒测速法的。从这个角度来看，位置差分测速法得到的速度的方差要优于多普勒测速和接收机输出速度，即整体速度的稳定性要优于多普勒测速和接收机输出。

（2）从中间细节方面来考虑，虽然汽车速度是人为大致控制在70km/h，但是由于现实情况的种种原因，汽车不可能长时间的做匀速运动，它的速度一定是变化的，但是肯定是在70km/h附近波动，即汽车实际上是做变速运动，可以看出多普勒测速和接收机输出速度能够实时反映汽车的速度，而它们的差值均值控制在毫米级，而和位置差分的差值均值为厘米级。

4 结束语

（1）位置差分测速法是假设物体做匀速运动的前提下的速度测量方法，所以该方法可以更好的反映匀速运动载体的速度情况，但是其受采样率的影响较大，而多普勒测速法基本不受采样率的影响。在2Hz以下甚至更高采样率的情况下，对于理想的匀速运动载体，位置差分测速法的精度要稍优于多普勒测速法。

（2）BDS数据的采集要充分考虑到高山、建筑物、树木以及高架桥的影响和干扰，以避免由于多路径效应等粗大误差的影响。

（3）由第一次测速和第二次测速尤其是第二次的结果可以推断出该导航型接收机输出的速度亦为经过多普勒方法计算得出，并且其精度和多普勒测速精度相差在毫米级。

（4）多普勒测速可实时反映载体速度的变化，测速精度主要取决于多普勒观测值的精度，不受载体运动状态和采样率高低的影响，实际生活中各种载体运动难以保证匀速性，因此，多普勒测速不失为一种高精度测速方法。

［1］何海波.高精度GPS动态测量及质量控制［D］.郑州：解放军信息工程大学，2002.

［2］肖云，孙中苗，程广义.利用GPS多普勒观测值精确确定运动载体的速度［J］.武汉测绘科技大学学报，2000，25（2）：113－117.

［3］张明，王宏涛，王强.利用 GPS多普勒观测值精确确定运动载体的速度［J］.电光与控制，2006，13（3）：98－101.

［4］何海波，杨元喜，孙中苗.几种 GPS测速方法的比较分析［J］.测绘学报，2002，31（3）：217－221.

［5］何海波，杨元喜，孙中苗，等.GPS多普勒频移测量速度模型与误差分析［J］.测绘学院学报，2003，20（2）：79－82.

［6］党超.基于北斗的航天器测姿、测速技术研究［D］.哈尔滨：哈尔滨工程大学，2012.

［7］ELLIOTT D K，CHRISTOPHER J H.GPS原理与应用［M］.寇艳红，译.2版.北京：电子工业出版社，2010：39－246.

［8］杨鑫春，徐必礼，胡杨.北斗卫星导航系统的星座性能分析［J］.测绘科学，2013，38（2）：8－11.