顾及接收机钟跳的北斗系统周跳探测方法

王俊杰，何秀凤

（1.河海大学 地球科学与工程学院，南京 210098；2.河海大学 卫星及空间信息应用研究所，南京 210098）

1 引言

严密的质量控制是确保卫星导航定位解连续、准确、可靠的重要保障。在高精度的全球卫星导航系统（global navigation satellite system，GNSS）数据处理中，周跳的探测与修复一直是个重要问题［1］，周跳探测与修复的正确性对于后续模糊度的确定以及最终定位结果的精度至关重要［2］。国内外学者提出了许多周跳探测与修复的方法，常用的有高次差法、多项式拟合法、相位减伪距法、电离层残差法、M－W（Melbourne－Wübbena）组合法以及各种星间或站间差分方法等［3-4］。然而接收机钟跳作为影响周跳探测的重要因素却很少引起关注，甚至有学者将其作为周跳处理［5-6］，严重影响数据处理的精度和效率。

接收机钟跳是为了保持接收机内部时钟与系统时间同步、控制接收机钟差漂移而人为引入的［7］。钟跳将导致所有观测到的卫星，所有频率上的伪距或相位观测值产生数值相同（距离单位）的阶跃，这与周跳有本质的区别［8］。钟跳对观测值的影响表现为三类：伪距阶跃、相位连续；伪距连续、相位阶跃；伪距和相位同时阶跃［7］。钟跳对周跳探测、精密定位极为不利，尤其是第一、二类钟跳，M－W组合法易将其探测为周跳，导致所有卫星的模糊度参数反复重新初始化；电离层残差法虽不会将其判断为周跳，但错误的模糊度先验信息将影响位置等参数的估计［8-9］。因此，进行周跳探测与修复时，需顾及接收机钟跳的影响，并对钟跳进行探测和修复。

北斗卫星导航系统（BeiDou navigation satellite system，BDS）是中国正在实施的自主发展、独立运行的全球卫星导航系统，研究BDS数据预处理技术对于完善BDS数据质量控制体系具有重要意义。本文从钟跳的特性出发，结合M－W组合法与电离层残差法，提出一种顾及接收机钟跳的组合周跳探测方法，并采用实测北斗系统数据验证该方法的有效性。

2 钟跳探测与修复

伪距和载波相位观测方程分别为

式中，P为伪距观测值，ρ为站星几何距离，c为光速，δtr为接收机钟差，δts为卫星钟差，I为电离层延迟量，T为对流层延迟量，εP为包含多路径效应影响与伪距观测噪声等综合误差，λ为载波波长，N为整周模糊度，εφ为包含多路径效应影响与载波相位噪声等综合误差。

对式（1）与式（2）分别在历元间求差，有

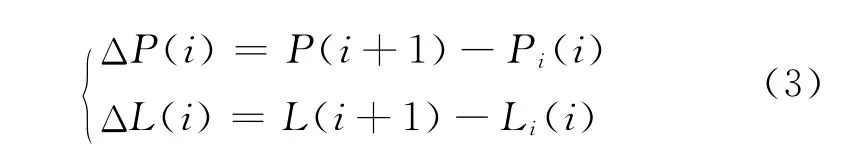
构造钟跳探测量S及其条件式

式中，i为历元，k1为阀值。对于某一历元，当且仅当所有可用卫星满足式（4）时，认为该历元时刻可能存在钟跳或所有卫星同时发生大周跳。此时利用式（5）计算钟跳候选值m，并依据毫秒级钟跳的整数特性，由式（6）进一步确定实际钟跳值Js，单位为ms。

式中，j为卫星；n为有效卫星数；k2为阀值，k2＝10－5～10－7。

由探测量S的表达式可知，该探测量不能区分第一、二类钟跳。为了进一步区分钟跳类型，应联合ΔP、ΔL按式（7）进行判断。

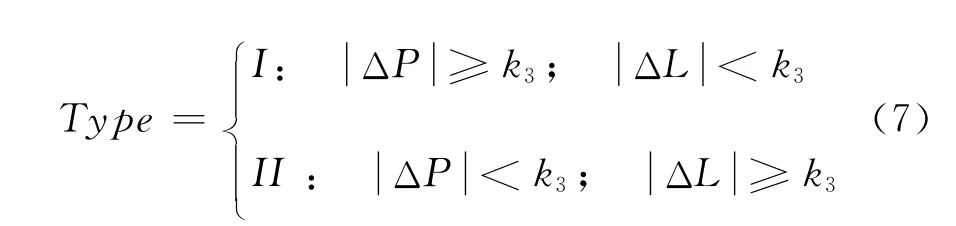
式中，k3为阀值，且k3＝k1－Δ，其中，Δt为采样率，为卫地距变化率。

采用反向修复法进行钟跳修复，即当发生第一类钟跳时，将连续的相位观测值调整成与伪距一样阶跃；当发生第二类钟跳时，将连续的伪距观测值修复成与相位一样阶跃。该方法有利于保持伪距和相位基准的一致性，而且不会破坏模糊度参数的连续性。其修复公式为

3 周跳探测的数学模型

3.1 M－W组合法

M－W组合法广泛应用于周跳探测［10］，其表达式为

式中，λMW＝c/（f1－f2）≈86cm，NMW＝N1－N2。λMW和NMW分别被称为宽巷波长和宽巷模糊度。因此，宽巷模糊度可表示为

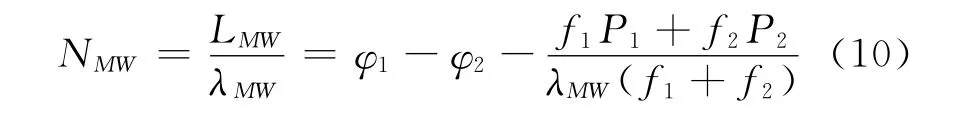
在式（10）中，通过宽带组合消除了几何距离部分、电离层影响和系统误差，只剩下模糊度项。假设L1和L2的周跳分别为ΔN1和ΔN2，对M－W组合观测值在历元间求差有

采用递推法求NMW的均值和标准差

式中，＜NMW＞i为前i个历元的平均值，σi为前i个历元的标准差。

若 ｜NMW（i）－ ＜NMW＞i-1｜ ≥4σi且｜NMW（i＋1）－NMW（i）｜≤1成立，则认为历元i－1和i之间有周跳；｜NMW（i）－＜NMW＞i-1｜≥4σi且｜NMW（i＋1）－NMW（i）｜≥1成立，则认为i为野值。

3.2 电离层残差法

电离层残差法利用双频载波相位测量的电离层残差进行周跳的探测，它主要考察不同历元间电离层残差的变化［11］。在双频相位观测方程之间求差，得

等式两边同时处除λ1，有

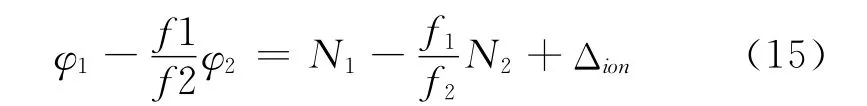
由式（15）可知，站星几何距离、接收机和卫星钟差都已消除，电离层延迟影响被大大减弱。假设L1和L2的周跳分别为ΔN1和ΔN2，对式（7）在历元间求差，则周跳部分的估计量为

根据式（16），按照方差协方差传播定律有

假设L1和L2的测量误差均为m＝±0.01周，代入北斗系统的频率值计算得mD＝±0.023周。取3倍标准差±0.07周作为限差，即当式（16）中周跳部分估计量超过0.07周时，判断为发生周跳。

4 周跳探测与实验分析

4.1 周跳探测组合方法

M－W组合不受电离层影响，能有效探测1周以上的周跳［10］，但当两个载波频率上发生的周跳满足ΔN1＝ΔN2时，该方法失效。电离层残差法仅采用载波相位观测值，精度高，可探测出小周跳，但当两个载波频率上发生的周跳满足ΔN1f2＝ΔN2f1时，该方法同样失效。此外，当探测到周跳时，单独利用M－W组合法或电离层残差法均不能判断周跳发生在哪个频率上。因此，应充分利用上述两种方法的特点，优势互补，将二者组合进行周跳探测。

前以述及，M－W组合法易将第一、二类钟跳探测为周跳，严重影响数据处理精度。故在采用M－W组合法进行周跳探测时，应先进行钟跳的探测与修复。但周跳的存在，尤其是大周跳会对钟跳探测造成不利影响。综合考虑以上因素，提出一种顾及接收钟跳的周跳探测方法，具体步骤如下：

①采用对钟跳不敏感的电离层残差法逐卫星进行周跳探测，一旦发现周跳，剔除该卫星发生周跳的历元；

②进行钟跳探测，若存在钟跳则计算出钟跳值，并采用反向修复法进行修复；

③对钟跳修复完的观测值运用M－W组合法并结合电离层残差法的探测结果进行周跳修复。

4.2 实验分析

采用2012－10－01印尼巴东地区实测北斗系统C03号星进行实验。图1和图2分别为该测站钟跳修复前与修复后的BDS原始观测值及其周跳探测时序。由于C1与C2观测值很接近，故图中只表示C1观测值。关于周跳标记，其中 “0”表示无周跳，“1”表示有周跳。

图1 钟跳修复前C03卫星周跳探测结果

图2 钟跳修复后C03卫星周跳探测结果

由图1和图2可以看出，钟跳修复前伪距阶跃而相位连续，接收机钟跳为第一类钟跳，经钟跳探测得其钟跳为1ms。采用M－W组合法与电离层残差法的组合方法对钟跳修复前的数据进行周跳探测，所有钟跳历元均被误探为周跳，验证了M－W组合法易将钟跳探测为周跳的结论。钟跳修复后，伪距和相位同时阶跃，正是第三类钟跳的情形，这也说明第三类钟跳无需修复。

周跳的发生具有随机性，发生钟跳的历元可能同时兼有周跳。针对M－W组合法及电离层残差法各自的局限，分别在不同的钟跳历元及普通历元上模拟了（1，1），（1，0），（0，－1），（－77，－60），（763，590）等特殊的周跳组合，其中，（763，590）是由北斗系统载波频率根据关系式ΔN1f2＝ΔN2f1导出的。各周跳组合的探测及修复结果如表1所示。由表1可知，无论周跳发生在普通历元还是钟跳历元，所提出的组合周跳探测方法均能探测出周跳。普通历元的周跳浮点解与真实周跳值接近，通过四舍五入取整可得到正确的周跳值；钟跳历元的周跳浮点解与真实周跳值存在较大差异，四舍五入取整可能得到错误的周跳值，可通过构造整数搜索空间的方法获取正确的周跳值。

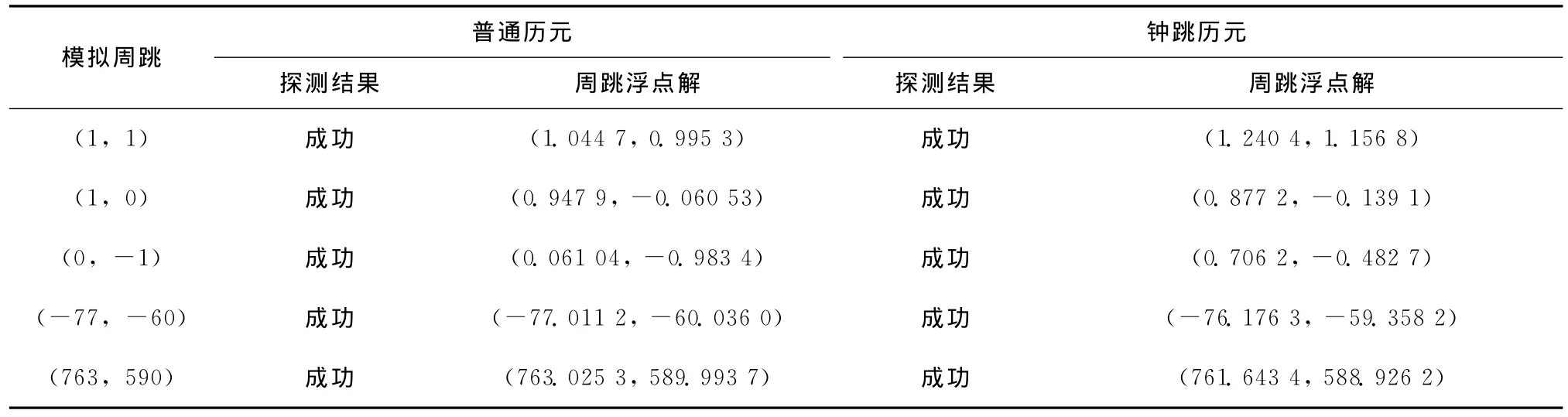
表1 C03号星周跳探测与修复结果

5 结论

为了克服接收机钟跳对周跳探测的影响，提高数据处理的精度和效率，本文提出一种顾及接收机钟跳的周跳探测方法，通过M－W组合法、电离层残差法及钟跳探测与修复方法的有机组合，实现了含有钟跳的观测数据的周跳探测与修复，并采用印尼巴东地区实测北斗系统数据验证了该方法的有效性。无论周跳发生在普通历元还是钟跳历元，该方法均能成功探测周跳，周跳的修复时采用整数搜索空间的方法可提高修复的正确率。该组合周跳探测方法虽是基于BDS提出，但也可应用于其他卫星导航系统的数据预处理，为导航定位等方面的应用提供良好的质量控制。

［1］蔡昌盛，高井祥.GPS周跳探测及修复的小波变换法［J］.武汉大学学报：信息科学版，2007，32（1）：39－42.

［2］王成，王解先.单频非差相位观测值的周跳探测与修复方法［J］.同济大学学报：自然科学版，2012，40（9）：1393－1398.

［3］XU Guo－chang.GPS Theory，Algorithms and Applications［M］.2nd ed.Berlin：Springer－Verlag，2007.

［4］李征航，张小红.卫星导航定位新技术及高精度数据处理方法［M］.武汉：武汉大学出版社，2009.

［5］喻国荣.基于移动参考站的GPS动态相对定位算法研究［D］.武汉：武汉大学，2003.

［6］杨剑，王泽民，王贵文，等.GPS接收机钟跳的研究［J］.大地测量与地球动力学，2007，27（3）：123－127.

［7］郭斐，张小红.在线服务系统对钟跳的处理能力分析［J］.武汉大学学报：信息科学版，2012，37（11）：1333－1336.

［8］张小红，郭斐，李盼，等.GNSS精密单点定位中的实时质量控制［J］.武汉大学学报：信息科学版，2012，37（8）：940－944.

［9］于合理，郝金明，刘伟平，等.接收机钟跳对周跳探测的影响及探测方法［C］//第四届中国卫星导航学术年会论文集，武汉：中国卫星导航学术年会组委会，2013.

［10］LIU Zhi－zhao.A New Automated Cycle Slip Detection and Repair Method for a Single Dual－frequency GPS Receiver［J］.Journal of Geodesy，2011，85（3）：171－183.

［11］刘基余.GPS卫星导航定位原理与方法［M］.北京：科学出版社，2008.