广义高阶Bernoulli多项式的一些恒等式及其应用
王念良
(商洛学院 数学与计算机应用学院/应用数学研究所,陕西商洛726000)
广义高阶Bernoulli多项式的一些恒等式及其应用
王念良
(商洛学院 数学与计算机应用学院/应用数学研究所,陕西商洛726000)
Bernoulli多项式及其多种推广形式在组合数学、解析数论等领域中起着十分重要的作用。广义Bernoulli多项式Bn,χ(x)与Euler多项式、Dirichlet级数有密切的联系。应用绝对收敛Laurent级数的卷积公式,给出了广义高阶Bernoulli多项式的一些表达式和一个推论。
Bernoulli数;广义高阶Bernoulli多项式;Laurent级数
1 引言与结论
设q是大于1的正整数,χ是模q的Dirichlet特征。广义高阶Bernoulli数、广义高阶Bernoulli多项式分别定义[1]为:


广义Bernoulli数能给出Dirichlet L函数在0和负整数处的值[2]Bernoulli数、Bernoulli多项式及其推广形式,在解析数论、组合数学中有着十分重要的地位,吸引了许多国际、国内学者、专家的研究兴趣,得到了很多有趣的结论,部分内容读者可参阅文献[1-17]。本文应用第一类stirling数s(m,k),Dirichlet级数在s=-n,(n∈Z,n≥0)处的值,给出了广义高阶Bernoulli多项式的一些卷积和公式,并由此得到了广义高阶Bernoulli数的一个恒等式,即


2 定理的证明


这就证明了定理1。
推论1的证明由定理1和(1)式、(2)式,显然结论成立。
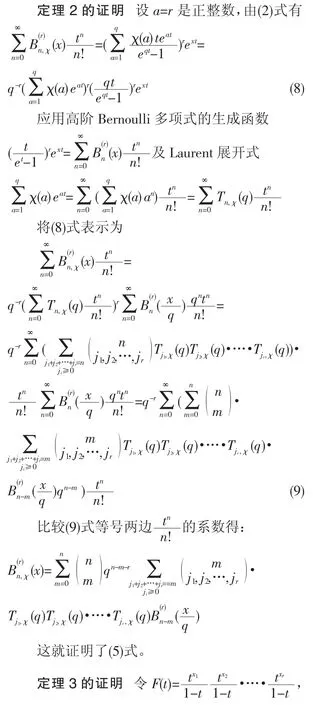

[1]Wang N,Li C,Li H.Some identities on the Generalized Higher-order Euler and Bernoulli numbers[J].Ars Combinatoria,2011,2:517-528.
[2]Chen K W.Sums of products of Generalized Bernoulli polynomials[J].Pacific Journal of Mathematics,2003, 208(1):39-52.
[3]Ireland K,Rosen M.A classical introduction to modern number theory,graduate texts in mathematics[J].Springer,New York,1990,84(2):394.
[4]Tom M.Apostol,introduction to analytic number Theory[M].Springer-Verlag,New York,1976:265.
[5]王念良.关于广义Bernoulli数的一些恒等式[J].内蒙古师范大学学报:自然科学汉文版,2014,43(4):403-407.
[6]Liu G,Luo H.Some identities involving Bernoulli numbers[J].The Fibonacci Quarterly,2005,43(3):208-212.
[7]Liu G.On congruences of Euler numbers modulo an square[J].The Fibonacci Quarterly,2005,43(2):132-136.
[8]王念良,李复活.高阶Apostol-Bernoulli函数的—些恒等式[J].商洛学院学报,2011,25(6):3-6.
[9]Kanebo M.A recurrence formula for the Bernoulli numbers[J].Proc Japan Acad Ser A Math Sci,1995,71:192-193.
[10]Lehmer E.On congruences involving bernoulli numbers and the quotients of fermat and Wilson[J].Annals of Math,1938,39:350-360.
[11]Eie M,Lai K F.On Bernoulli identities and appilications[J].Rev Mat Iberoamericana,1998,14(1):167-213.
[12]Kanemitsu S,Ubanowicz J,Wang N.On some new congruences for generalized Bernoulli numbers[J].Acta Arith,2012,155(3):247-258.
[13]Yuan Y.Some identities involving Bernoulli numbers and Euler numbers[J].Scientia Magna,2006,2(1):102-107.
[14]何 园,张文鹏.关于一个多项式序列的对称关系[J].西南师范大学学报:自然科学版,2013,38(4):28-30.
[15]巫朝霞,何 园.关于Bernoulli和Euler多项式的一个注记[J].内蒙古师范大学学报:自然科学汉文版, 2012,41(6):604-606.
[16]Szmidt J,Urbanowicz J,Zagier D.Congruences among generalized Bernoulli numbers[J].Acta Arithmetica,LXXI, 1995,3:273-278.
[17]雒秋明.广义Bernoulli数和广义高阶Bernoulli数[J].纯粹数学与应用数学,2002,18(4):305-308.
(责任编辑:李堆淑)
Some Identities Involving Generalized Higher-order Bernoulli Polynom ials and Its Applications
WANG Nian-liang
(College of Mathematics and Computer Application,Shangluo University/Institute of Applied Mathematics,Shangluo 726000,Shaanxi)
Bernoulli polynomials and its variety generalizations play a central role in the theory of Combination and Analytic Number Theory.It is well-known that the generalized Bernoulli polynomial Bn,χ(x)closely related to Euler polynomials and Dirichlet series.By the product formulas of the absolute convergence Laurent expansion,a representation of generalized Higher-order Bernoulli polynomial and a corollary are obtained.
Bernoulli number;generalized higher-order Bernoulli polynomial;Laurent series
O156.4
:A
:1674-0033(2014)06-0003-03
10.13440/j.slxy.1674-0033.2014.06.001
2014-09-28
陕西省教育厅专项科研计划项目(2013JK0570)
王念良,男,陕西商州人,博士,教授

