BP神经网络在多维非线性函数拟合中的应用

刘俊

（商洛学院 电子信息与电气工程学院，陕西商洛726000）

BP神经网络在多维非线性函数拟合中的应用

刘俊

（商洛学院 电子信息与电气工程学院，陕西商洛726000）

为了解决常规方法拟合多维非线性函数的预测结果精度较低问题，采用非线性映射能力较强的BP神经网络进行多维非线性函数拟合。通过对BP神经网络结构及训练过程的分析，依据给定的两维非线性函数构建BP神经网络模型，并利用MATLAB软件对BP神经网络进行预测。仿真结果表明，BP神经网络对于两维非线性函数有良好的拟合能力，拟合误差小、收敛速度快，也使该方法具有较好的推广性。

函数拟合；BP神经网络；多维非线性函数

BP（Back Propagation）神经网络是一种误差反向传播的多层前馈神经网络，由Rumelhart和McCelland等学者在1986年提出的。经过近30年的研究和改进，BP神经网络已经形成了一套完善的理论体系，同时在模式识别、数据压缩等领域有良好的应用[1-5]，也是目前应用最广的人工神经网络模型之一。

在科学实验和工程应用中，常会遇到一些复杂的非线性系统，难以用准确的数学模型表示这些系统测试数据中自变量与应变量之间的函数关系。邓晓敏等[6]把origin应用到处理非线性函数实验中，该方法适用于数据量较小、非线性程度较低的实验中。唐佳德[7]介绍了MATLAB软件自带非线性拟合函数lsqcurvefit、lsqnonlin和非线性曲线图形窗口，该方法对于复杂映射和多维映射拟合精度较低。李初晔等[8]采用多参数有限元技术拟合函数，该方法最终要找到具体的函数表达式，而对于非线性程度高的函数就无法精确表示。董锐[9]把BP神经网络、RBF神经网络和样条神经网络应用到非线性函数逼近领域，取得了良好效果。本文为了解决常规方法拟合多维非线性函数的预测结果精度较低问题，提出基于BP神经网络的多维非线性函数拟合，该方法能够快速学习和记忆大量的输入——输出之间的映射关系，不需要具体的映射关系数学方程，能够很好地表达这些复杂的非线性函数。通过BP神经网络的建模、训练、预测仿真实验，结果能够满足预期效果。

1 BP神经网络

1.1 BP神经网络结构

BP网络是一种多层前馈神经网络，由输入层、隐含层和输出层组成，隐含层可以有一层或多层。该网路具有较强的非线性映射能力，图1为一个典型的单隐含层的BP网络结构图。图1中x1，x2，…，xm为输入层各神经元的实际输入；ωij为隐含层第i个神经元与输入层第j个神经元间的权值；g(·)为隐含层的激励函数；α1，α2，…，αq为隐含层各神经元阈值；ωki为输出层第k个神经元与隐含层第i个神经元间的权值；β1，β2，…，βn为输出层各神经元阈值；f(·)为输出层的激励函数；y1，y2，…，yn为输出层各神经元的实际输出；ek为网络的输出误差[10]。

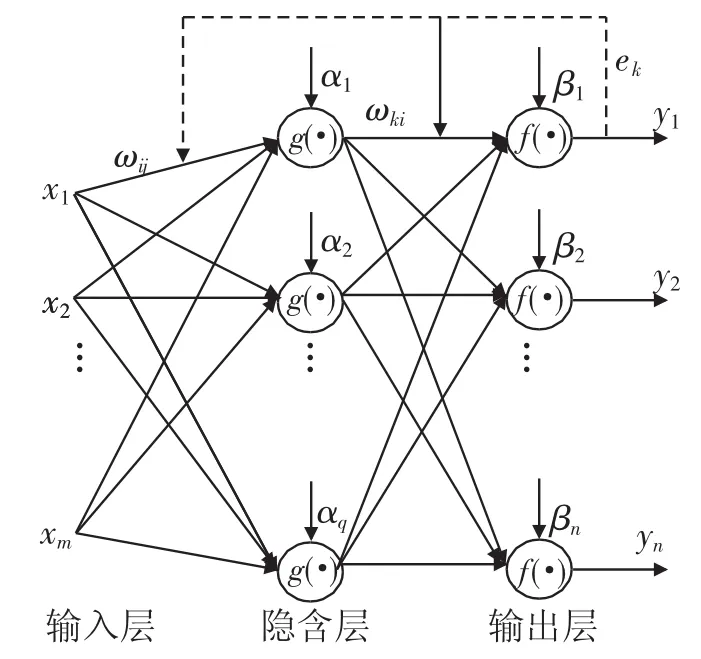
图1 典型单隐含层BP神经网络结构图

1.2 网络训练过程

网络训练分为以下两个过程[11]：

第一个过程是工作信号前向传播。样本数据作为输入信号经各隐含层逐层传输，并根据随机初始化设定的一组网络权值和阈值来计算，最后把隐含层计算结果传向输出层，并利用激励函数和输出阈值计算得到相应的输出值。

第二个过程是误差信号反向传播。输出层计算结果与期望值比较，若误差不满足要求，误差信号返回到输入层和隐含层，利用梯度最速下降法，调整各层的阈值和权值。这两个过程反复进行，直到网络误差达到最小或人们所期望的值，网络训练结束。图2为BP网络训练流程图。

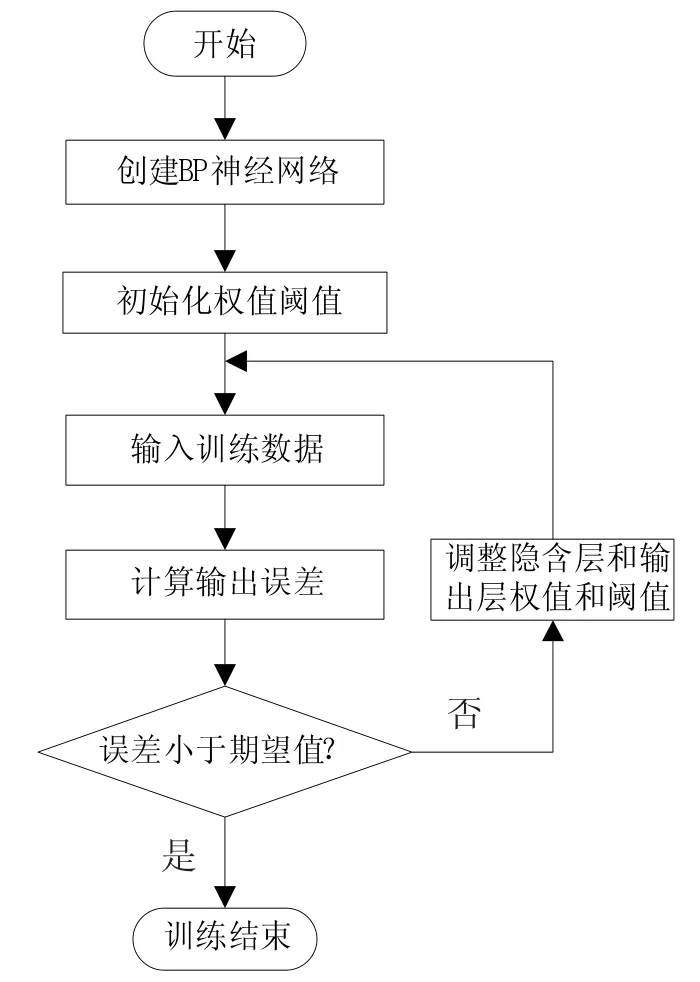
图2 BP神经网络训练过程

2 BP神经网络设计

本文利用BP神经网络拟合的两维非线性函数为：

2.1 输入层和输出层神经元数目的选择

BP神经网络的输入层和输出层神经元数目通常根据求解方程和系统数据来源而定。选择原则是在满足网络精度的前提下，尽可能减小系统规模，减小系统学习时间和复杂性。本文拟合非线性函数有两个输入参数（x和y），两个输出参数（z1和z2），所以输入选择2个神经元，输出选择2个神经元。

2.2 隐含层层数的选择

理论上已经证明具有单S型隐含层和单线性输出层的BP神经网络可以逼近任意非线性系统[12]。多隐含层可以增强泛化能力，提高预测精度，但是训练时间较长。隐含层层数的选择要综合考虑训练时间和网络精度，对于复杂的非线性系统，则可以考虑多隐含层，牺牲训练时间，以满足精度要求；但对于简单的非线性系统，在满足网络精度的前提下，可以采用单隐含层，以加快速度。本文拟合的非线性函数较为简单，选择单隐含层。

2.3 隐含层神经元数目的选择

隐含层神经元数目的选择对网络性能影响较大。隐含层神经元数目太少，不能实现很好的数据映射关系，无法满足网络精度要求；隐含层神经元数目太多，常出现过拟合现象。通常情况，网络预测精度随着隐含层神经元数目的增加呈现先提高后降低的趋势。在具体应用时，一般采用尝试法选择最合适的神经元数目。本网络经过多次测试，选择10个隐含层神经元，可以达到较高精度要求。

3 MATLAB仿真实现

3.1 BP神经网络构建

利用MATLAB神经网络工具箱中的newff函数构建一个BP神经网络，隐含层和输出层的传输函数选择‘tansig’，该函数为S型函数，理论上，只要选择合适的权值和阈值，可以逼近任意非线性函数。网络训练函数选择‘trainlm’，该算法采用数值优化技术，具有收敛速度快、稳定性高等优点。权值学习函数选择‘learngdm’，该算法梯度下降动量动态寻优算法，可以减小学习过程的振荡趋势，改善收敛性。

3.2 BP神经网络训练

本文根据式(1)随机生成150组输入/输出数据，从数据中随机选择100组数据用作BP神经网络的训练数据，其余50组数据作为网络测试数据使用。网络训练目标最小误差为5-10，最大训练次数500次，学习速率设置为0.1。BP神经网络训练函数采用MATLAB神经网络工具箱中的train函数。

3.3 BP神经网络测试

把50组训练数据中的输入样本输入到训练好的BP神经网络，得到网络预测输出值，通过与期望输出值比较，分析BP神经网络的拟合能力。

3.4 结果与分析

训练后的BP神经网络经网络测试得到误差变化过程曲线如图3所示。运行时间迭代157次后，网络预测精度达到设定要求。

图3 网络训练误差随迭代次数变化

网络预测输出值与期望输出值比较如图4所示，为了更清晰显示BP神经网络在非线性系统中的拟合能力，图5和图6给出了预测输出与期望输出误差和预测误差百分比，从图5和图6中可以看到误差百分比的绝对值在1%以内，表明BP神经网络对两维非线性函数具有较高的拟合能力。

图4 BP神经网络预测输出与期望输出的比较

图5 BP神经网络预测误差

图6 BP神经网络预测误差百分比

4 结语

本文将BP神经网络应用到多维非线性函数拟合问题中，同时利用MATLAB软件自带的神经网络工具箱函数，免除编写复杂庞大程序的困扰，同时具有调试方便、运行效率高等优点。

通过对给定的两维非线性函数进行MATLAB仿真实验，验证了BP神经网络具有较高的非线性函数拟合能力，为多维非线性函数拟合提供了一种可靠、高效的拟合方法，具有一定的推广和应用价值。

[1]张雨浓,蔡炳煌.人工神经网络研究进展及论文发表过程[M].北京：电子工业出版社,2010：96-99.

[2]蒋正金,汪晓东,端木春江.采用BP神经网络拟合光纤位移传感器特性曲线[J].微型机与应用,2012,31(4)：67-69.

[3]郑建华.图像数据压缩的BP神经网络方法研究[J].计算机仿真,2001,18(2)：33-35.

[4]王泰刚.基于神经网络的手写字符识别系统[D].大连：大连海事大学,2013：28-35.

[5]方一新.改进BP神经网络的EMG手指运动识别[J].激光杂志,2014,35(9)：92-95.

[6]邓晓敏,张军朋,吴先秋.利用origin确定实验中非线性函数的曲线关系[J].大学物理实验,2011,24(1)：73-76.

[7]唐家德.基于MATLAB的非线性曲线拟合[J].计算机与现化,2008(6)：15-19.

[8]李初晔,邓 凌,马 岩.多参数有限节点函数拟合技术[J].青岛理工大学学报,2013,34(1)：107-112.

[9]董 锐.基于神经网络的函数逼近方法研究[D].吉林：东北师范大学,2011：21-29.

[10]刘 冰,郭海霞.MATLAB神经网络超级学习手册[M].北京：人民邮电出版社,2014：159-160.

[11]吴正茂,罗 健.利用BP神经网络实现函数逼近[J].长江工程职业技术学院学报,2005(2)：50-52.

[12]Kreino V Y.Arbitrary nonlineartity of sufficient to represent all functions by neural[J].Networks：A Theorem N N,1991(4)：381.

（责任编辑：李堆淑）

The Application of BP Neural Network in Multidimensional Nonlinear Function

LIU Jun
(College of Electronic Information and Electrical Engineering,Shangluo University,Shangluo 726000, Shaanxi)

In order to solve the low precision prediction problem in conventional method of multidimensional nonlinear function fitting,the strong non-linear mapping of BP neural network in multidimensional nonlinear function fitting is applied.By analyzing the BP neural network structure and training process,BP neural network model is established by the given two dimensional nonlinear,and prediction about BP neural network is made with MATLAB software.The simulations reveal that the application of BP neural network in two dimensional nonlinear function enjoys higher accuracy of fitting and fast convergence speed,which make it possible to generalize it.

function fitting;BP neural networks;multidimensional nonlinear function

TP183

：A

：1674-0033（2014）06-0019-04

10.13440/j.slxy.1674-0033.2014.06.007

2014-10-09

刘 俊，男，山西大同人，硕士，助教