基于改进2D-DLPP算法的人脸识别
马家军
(商洛学院 数学与计算机应用学院,陕西商洛726000)
基于改进2D-DLPP算法的人脸识别
马家军
(商洛学院 数学与计算机应用学院,陕西商洛726000)
在二维局部保持投影中引入类间结构信息和类标签,得到有监督的二维判别局部保持投影算法,从而提高了特征集的鉴别性。针对算法中参数的选取问题,建立无参数权重矩阵,提出无参数的二维判别局部保持投影(无参数2D-DLPP)算法。在Yale和ORL人脸库上的仿真实验结果表明,该算法与二维判别局部保持投影(2D-DLPP)、二维局部保持投影法(2D-LPP)和二维线性判别分析法(2D-LDA)相比能够取得更高的识别率。
人脸识别;特征提取;二维判别局部保持投影;无参数
特征提取是模式识别领域关键技术之一,其通过一定的数学变换将高维数据转化为低维数据,在保持高维数据流形结构前提下对数据进行压缩。Turk[1]和Kirby等[2]首次提出了主成分分析人脸识别方法,并取得了成功。
有研究表明[3-4]图像位于高维图像空间的低维流形之上,二维局部保持投影(2D-LPP)算法[5]考虑了邻域内局部信息,而没有考虑邻域间局部信息。这只能使同一类内的样本在降维后尽可能地接近,而不能使不同类的样本在降维后尽可能地隔远。因此,为了具有更好的判别性,在2D-LPP中引入类间约束信息,提出二维判别局部保持投影(two-dimensional discriminant locality preserving projections and face recognition, 2D-DLPP)算法[6-7]降维后的样本类内局部散度最小,同时类间局部散度最大。但构造2D-DLPP的相似矩阵时涉及到参数的选择,较为复杂。为此,提出一种新的算法:无参数二维判别局部保持投影(parameter-less two-dimensional discriminant locality preserving projections 2D-DLPP)算法。
1 二维判别局部保持投影算法
假设x1,x2,…,xN是m×n维欧氏空间Rm×n中的N个训练样本,共有C个类别,每个类对应的样本数量为n1,n2,…,nc一般的二维线性特征提取方法是把图像矩阵向A上投影:

其中A∈Rn×d是按照某种优化准则得到的投影矩阵,y∈Rm×d(d<n)代表x的特征矩阵。
二维判别局部保持投影(2D-DLPP)算法的目标函数为:
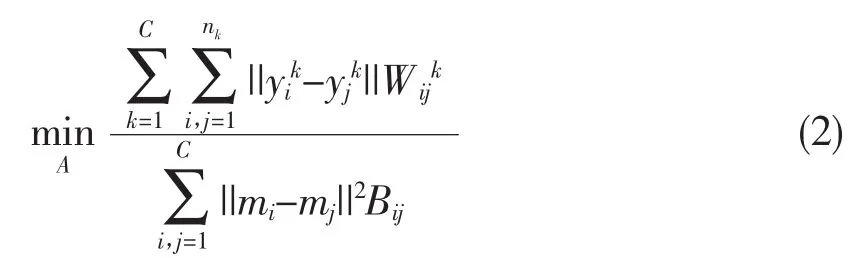
由式(1)和式(2),2D-DLPP的目标函数可以表示为:
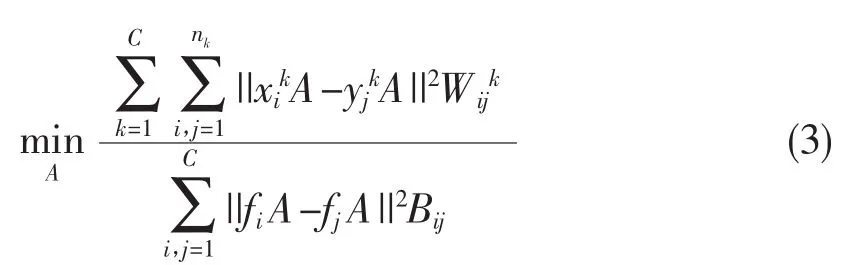

t>0是由经验确定的参数,B为类间相似矩阵, Bij表示第i类与第j类的平均样本fi和fj的相似度,它定义为:,类似于类内相似度,t>0同样是需要确定的参数。
通过代数运算,目标函数式(3)化简为:

X=[(x11),…,(x1n1),…,(xk1),…,(xc1),…,(xcnc)]∈Rm×nN为训练样本空间;F=[f1,f2,…,fc]∈Rm×nC为平均样本空间;L=D-W,D=diag(D1,D2,…,Dk,…,DC), W=diag(W1,W2,…,Wk,…,WC),Dk为对角矩阵,其第i个对角元素为的第i行元素求和,即;H= E-B,E为对角矩阵,;Im是m阶的单位矩阵;运算符⊗为矩阵的克罗内克积。
要求满足目标函数的投影矩阵A,只需求解特征方程:SHA=λSLA,得到特征值λ对应的特征向量构成的矩阵A。
观察目标函数的表达式可知,其分子表示投影后的类内离散度,分母则表示投影后的类间离散度。目标函数的最小化就是在投影后使得在同一类的样本最接近,同时使不同类的样本尽可能隔得最远。
2D-DLPP是在2D-LPP中引入判别信息得到的,因而为监督算法。它保留了局部保持的特征,同时反映了人脸图像的流形结构。因此,2D-DLPP优于其它的统计类方法。但2D-DLPP面临复杂的参数选择。在计算类内相似矩阵、类间相似矩阵时需要确定各自的参数,通常分别取类内或类间样本平均距离。但参数的选择会影响2D-DLPP刻画样本的流形结构的精度,并且耗费较多的时间。因此,本文提出了无参数二维判别局部保持投影算法。
2 无参数2D-DLPP
2.1 无参数2D-DLPP数学定义
2D-DLPP使用欧氏距离刻画样本点的相似程度,两点间的欧氏距离越小,相似度越大,欧式距离越大,则相似度越小。在无参数2D-DLPP的相似矩阵中引入皮尔逊相关系数(又称简单相关系数)。皮尔逊相关系数描述了两个数据间联系的紧密程度,它可以看作是两个随机变量中的样本集向量之间夹角的余弦函数。文献[8]表明欧氏距离对离散数据点的选取依赖性较强,而余弦距离在离散数据中的鲁棒性更强。
令pij表示任意两个样本xi和xj之间的皮尔逊相关系数,pij的取值在-1与+1之间,pij的绝对值越大表明两个样本间的相关性越强;若pij=0则表明两个样本不是线性相关。将皮尔逊系数转化为属于区间[0,1]的样本间相似度:

则第k类内相似矩阵可定义为:

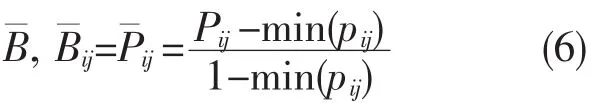
2D-DLPP的目标函数为:
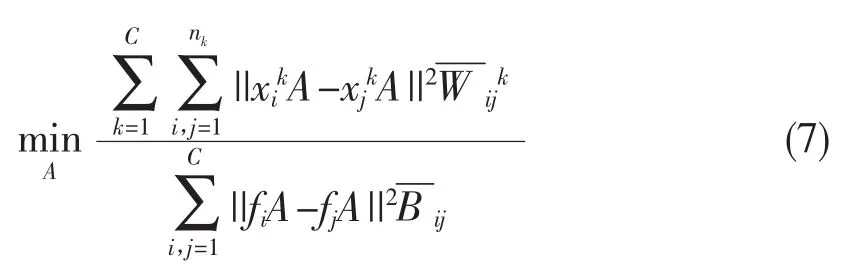
目标函数式(7)的分子可化简为:
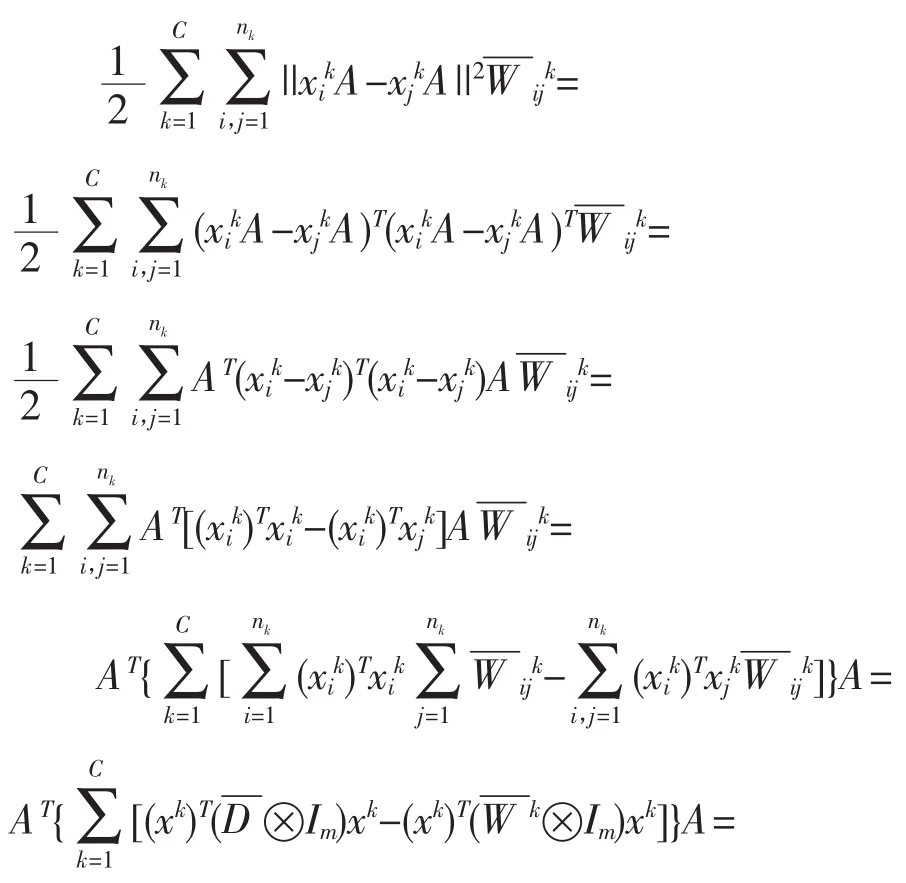

2.2 算法步骤
Step1获取训练样本集:
X=[(x11),…,(x1n1),…,(x1k),…,(xknk),…,(x1C),…,(xCnc)],共有N个训练样本,分为C个类别,每个类对应的样本数量为n1,n2,…,nC,其中xik∈Rm-n代表第k类中的第i个训练图像矩阵。
Step2通过式(5)和式(6)分别计算类内样本和类间样本的相似度,然后分别构造类内和类间相似矩阵。
Step4计算矩阵L和H,L=D-W、H=E-B。
Step5求解特征方程SHA=λSLA的d个最大特征值对应的d个特征向量a1,a2,…,ad。
Step5令A=[a1,a2,…,ad],对训练样本和测试样本进行投影。
Step6利用分类器对投影后的样本进行分类并分析结果。
3 实验结果与分析
为了验证本文算法的有效性,本文分别在Yale人脸库和ORL人脸库上进行仿真实验。实验前,所有的人脸图像都经过手动眼睛定位、校准,最终为归一化的图像。为了对比,同时使用2D-DLPP、2D-LPP、2D-LDA三种二维算法进行特征提取。在运行2D-LPP时,第k类内样本的相似度Wijk中的参数t通常取第k类中任意样本间距离的平均值;类似的,任意两类平均样本间的相似度Bij中的参数t通常取任意两个平均样本间距离的平均值。最后分别使用欧氏距离分类器和皮尔逊系数最近邻分类器对样本进行分类,并对比分类结果。
3.1 ORL人脸库试验
ORL人脸库包含来自40个不同人的400幅图像,每人有10幅大小、姿态、表情各异的图像。ORL人脸库主要用来测试本文算法在人脸图像大小、表情和姿态都变化时的识别性能。在实验中,分别使用基于欧氏距离和皮尔逊系数的最近邻分类器,研究特征值数目变化时,本文算法、2D-DLPP、2D-LPP和2D-LDA在ORL人脸数据库上正确识别率的变化情况。其中选取每人训练样本数为5。
图1为各算法使用基于欧氏距离的最近邻分类器进行分类,识别率随特征值数变化的曲线图;图2为各算法使用基于皮尔逊相关系数的最近邻分类器进行分类,识别率随特征值数变化。由图1与图2可知,无参数2D-DLPP在两种分类器中,相同维数情况下的识别率高于2D-DLPP、2D-LPP和2D-LDA,从而验证了本文算法的有效性。
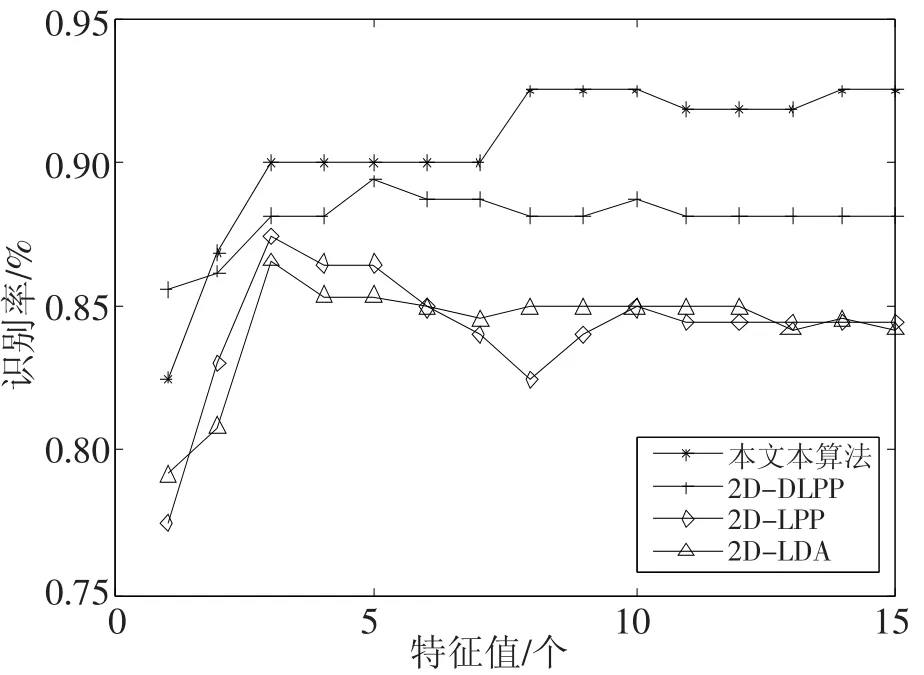
图1 欧氏距离分类器下各算法的识别率与特征值数的关系
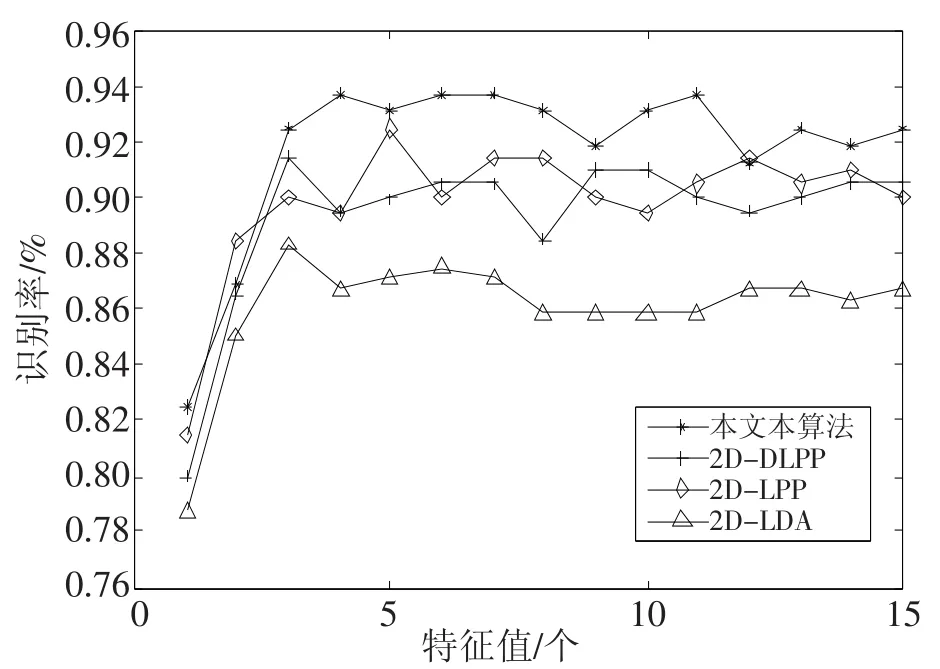
图2 皮尔逊相关系数分类器下各算法的识别率与特征值数的关系
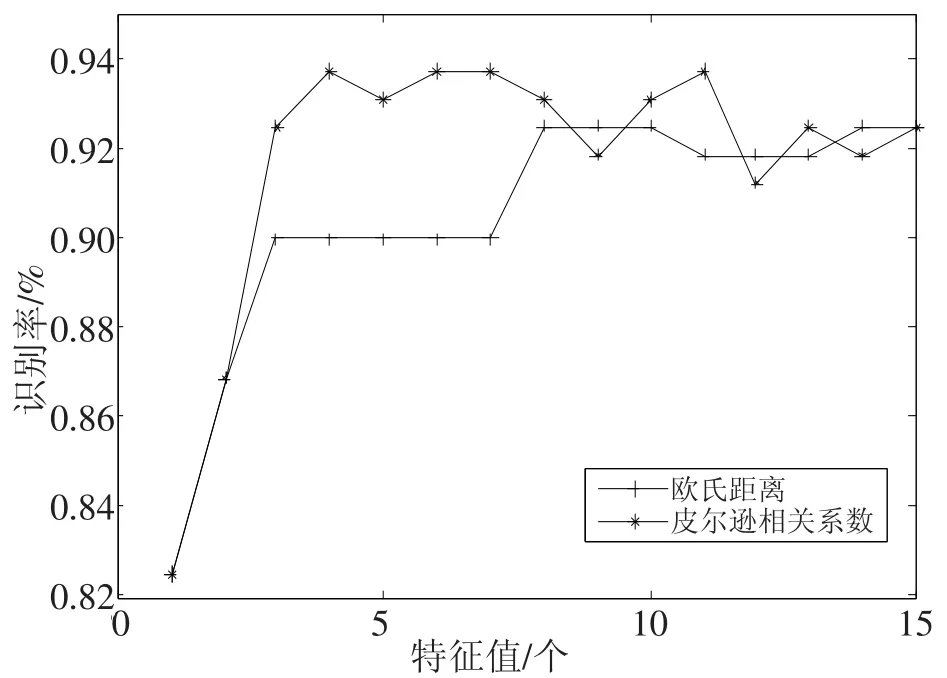
图3无参数2D-DLPP在不同分类器下识别率与特征值数的关系
图3则为无参数2D-DLPP分别使用基于欧氏距离和皮尔逊相关系数的最近邻分类器进行分类,识别率随特征值数变化。可以看出,使用基于皮尔逊相关系数的最近邻分类器进行分类时,其识别率比基于欧氏距离的最近邻分类器高出1.25%,并且前者在特征值数为4时即达到最佳识别率,而后者在特征值数为8时才能达到最佳识别率。这说明使用基于皮尔逊相关系数的最近邻分类器进行分类提高人脸识别率,同时大大降低计算复杂度。
3.2 Yale人脸库试验
Yale人脸库共有15个人,每人11幅图像,包含三种不同的光照情况,6种不同的表情,并且图像有戴眼镜和不戴眼镜的区别。
无参数2D-DLPP算法在YALE人脸库分别使用欧氏距离和皮尔逊相关系数的最近邻分类器进行分类,每人训练样本数为5。图4给出了识别率随特征值数变化。同样可以观察到,相较于基于欧氏距离的最近邻分类器,使用基于皮尔逊相关系数的最近邻分类器进行分类时有更高的识别率,其最高识别率比使用基于欧氏距离的最近邻分类器的最高识别率高出5.33%。可以说使用基于皮尔逊相关系数的最近邻分类器对提高Yale人脸库的识别率更有效。

图4 无参数2D-DLPP在不同分类器下识别率与特征值数的关系
验证不同算法在各个分类器上的最佳识别率。每人选择(n=4,5)幅图像作为训练集,余下的作为测试集。表1为各算法在YALE人脸库中采用最近邻分类器分类所取得的最佳识别率及对应的特征值,表1括号内为各算法取得最优识别率时的特征值,括号外的百分比为最优识别率。
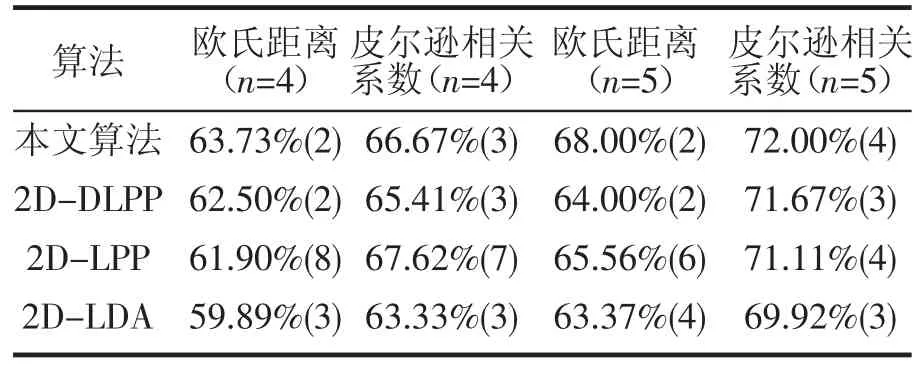
表1 YALE数据库上各算法最佳识别率及对应的特征值数
由表1可以看出,在训练样本数相同,采用以皮尔逊相关系数为度量的最近邻分类器进行分类时,各个算法有更好的识别效果,且本文算法(无参数2D-DLPP)识别率优于其它算法,再次证明了无参数2D-DLPP算法的有效性。
4 结语
本文在文献[8-9]的基础上,提出了无参数二维判别局部保持投影算法(无参数2D-DLPP)。无参数2D-DLPP不仅反映了投影后的邻域内局部信息,同时也反映了邻域间局部信息。并且在构造相似矩阵时不需要设置任何参数,通过皮尔逊相关系数度量样本间的相似度,使无参数2D-DLPP算法更加有效且对离散样本更具鲁棒性。最后在ORL和Yale人脸数据库上的实验验证了本文算法的优越性。
[1]Turk M,Pentland A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience,1991,3(1):72-86.
[2]Kirby M,Sirovich L.Application of the karhunen-loeve procedure for the characterization of human faces[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(1):103-108.
[3]龚 劬,马家军.基于改进二维保局投影算法的人脸识别[J].计算机工程,2014,40(9):252-256.
[4]Sam T,Roweis Saul K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290 (5500):2323-2326.
[5]Chen SB,Zhao H F,Kong M,et al.2DLPP:A two-dimensional extensionof localitypreservingprojections[J].Neurcompu-Ting,2007,70:912-921.
[6]Zhi R C,Ruan Q Q.Facial expression recognition basedon two-dimensionaldiscriminantlocality preserving projections[J].Neuro computing,2008,71:1730-1734.
[7]Yu WW.Two-dimensional discriminant locality preserving projections for face recognition[J].Pattern Recognition Letter,2009,30:1378-1383.
[8]殷 俊,周静波,金 忠.基于余弦角距离的主成分分析与核主成分分析[J].计算机工程与应用,2011,47(3):9-12.
[9]黄 璞,唐振民.无参数局部保持投影及人脸识别[J].模式识别与人工智能,2013,26(9):865-871.
(责任编辑:李堆淑)
Face Recognition Based on Improved 2D-DLPP Algorithm
MA Jia-jun
(College of Mathematics and Computer Application,Shangluo University,Shangluo 726000,Shaanxi)
By introducing between-class scatter constraint and label information into two-dimensional locality preserving projections(2D-LPP)algorithm,two-dimensional discriminant locality preserving projections(2D-DLPP)has more discriminant power than 2D-LPP.However,2D-DLPP is confronted with the difficulty of parameter selection,which limits its power on solving recognition problem.To solve this problem,by constructing parameter-less affinity matrix,an algorithm called parameter-less two-dimensional discriminant locality preserving projections(parameter-less 2D-DLPP)is proposed.The simulation results on Yale and ORL face database show that the method in this paper can get higher recognition rate than 2D-DLPP,2D-LPP and 2D-LDA.
face recognition;feature extraction;two-dimensional locality preserving projections; parameter-less
TP391.4
:A
:1674-0033(2014)06-0023-05
10.13440/j.slxy.1674-0033.2014.06.008
2014-10-05
马家军,男,陕西商南人,硕士,助教

