基于直觉模糊满意度模型的多级学生综合考评

鱼先锋

（商洛学院 数学与计算机应用学院，陕西商洛726000）

基于直觉模糊满意度模型的多级学生综合考评

鱼先锋

（商洛学院 数学与计算机应用学院，陕西商洛726000）

学生综合考评结果一方面反映高校学生管理水平和教学水平；另一方面反映不同学生在校综合表现优劣。基于直觉模糊满意度计算模型，确定四级评价指标体系和权重，结合实例对商洛学院某班学生进行了综合考评。将定性与定量的方法结合起来对学生综合考评,科学公正且自动化程度高，结果显示基于直觉模糊满意度的多级学生综合考评高效实用。

直觉模糊集；综合考评；指标体系

学生综合考评是学生管理中最具实际意义的工作之一。传统学生综合考评完全是手工统计分析,费时费力效率低下。考评过程以及复杂的考评结果分析常常令学生管理人员感到沮丧和难以把握，加之主观性强及指标体系复杂性,容易出错,难以保证考评的客观性和公正性，这样就出现了学生管理人员与学生间一些矛盾和问题,在不同程度上影响到了学生考评工作发挥其应有的作用,甚至对学生管理产生负面影响。直觉模糊集[1-3]（Intuitionistic Fuzzy Sets）理论由保加利亚学者K.T.Atanasssov提出,以其深刻的理论意义和广泛的实际背景；已被用于系统评价相关的各个领域[4-9]。文献[10]给出了直觉模糊满意度计算模型，该模型可用于解决多级综合评价问题。评价结果客观公正，评价过程自动化程度高且直觉模糊的方法自然的切近评价元数据。本文基于直觉模糊满意度计算模型，将定性与定量的方法结合起来对学生综合考评,科学公正且自动化程度高。分析了该模型的计算复杂度，并结合实例对商洛学院某班学生进行了综合考评，结果显示该模型高效实用。

1 直觉模糊满意度计算模型

文献[10]给出了直觉模糊满意度计算模型，计算了模型的复杂度;定义5给出了直觉模糊满意度计算模型，将对评价对象的满意、一般、不满意评价结果诱导到直觉模糊数的隶属度、犹豫度和非隶属度;定义4给出的模糊合成运算，做初级到高级评价的合成运算自然且自动化程度高;定理6指出，若用IFSD模型对n个对象做N个等级的IFSD计算,每一级有个m IFSD指标，则空间复杂度和时间复杂度都为O(nmk)，给出了详尽的证明，并说明了虽然该模型下空间复杂度和时间复杂度会随IFSD计算等级的增长呈指数增长，但实际中IFSD计算等级是比较小的值,所以不必担心复杂度过高。

2 学生综合考评应用案例

以商洛学院数学与计算机应用学院某班为例,根据班主任,辅导员,班委及该班30名学生的互评数据对该班学生应基于直觉模糊满意度计算模型进行多级学生综合考评。表1给出了评价过程中用到的指标体系及各级指标的权重(参照了《商洛学院学生综合素质考评实施办法（试行）》）。因为每个一级指标都包含了各个二级指标，因此一级指标不再列出。一级指标是班主任、辅导员、班委及该班30名学生互评的权重分别为0.5,0.3,0.2,0.1。

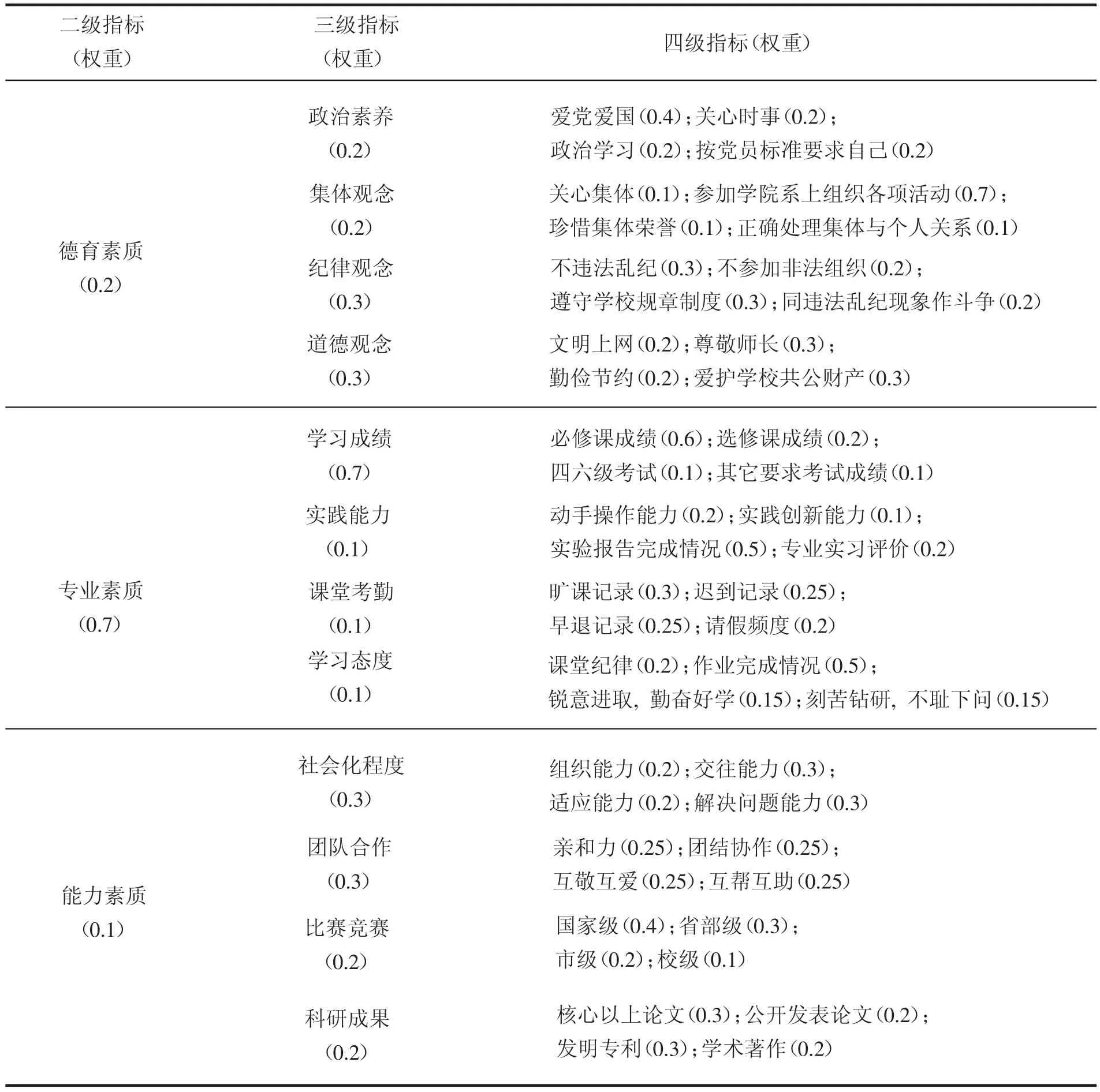
表1 指标体系与权重

同样过程计算1号学生“集体观念”“纪律观念”“道德观念”评价结果为,

R集1=（0.734,0.097,0.169），

R纪1=（0.789,0.087,0.124），

R道1=（0.889,0.092,0.019），

进行第三级评价,对1号学生“德育素质”进行评价,

归一化处理,

同样过程计算对1号学生“专业素质”“能力素质”评价结果为,

R专1=（0.872,0.103，0.025）

R能1=（0.446,0.027，0.517）

进行第二级评价计算对1号学生“学生互评”结果,

归一化处理,

同样过程计算对1号学生“班委评议”“辅导员评议”“班主任评议”评价结果为,

R委1=（0.834,0.097,0.169）,

R辅1=（0.729,0.087,0.184）,

R主1=（0.884,0.095,0.021）,

进行第一级评价计算对1号学生最终评价结果,

归一化处理,

g1无单位,它表征了对1号学生综合考评结果相对于其他学生的优劣,g1的值越大则说明1号学生表现越好。

同样过程对其他学生进行基于直觉模糊集的综合考评结果为，

G=（7.00,7.13,8.21,6.88,9.33,7.25,7.56,8.34, 6.27,6.51,9.00,8.30,8.26,7.74,8.55,7.71,8.64,7.29, 8.43,7.68,9.21,6.58,5.46,9.58,8.88,7.69,7.04,7.36, 8.49,8.27）

对综合考评得分按降序进行选择排序,结果为,

X=（24，5，21，11，25，17，15，29，19，8，12，30，13，3，14，16，26，20，7，28，18，6，1，4，22，10，9，23），x1=24说明第24号学生综合考评排名第一, x30=23说明23号学生综合考评成绩最差。

3 结语

基于直觉模糊满意度计算模型，选取了48个四级指标，12个三级指标，3个二级指标（德育素质、专业素质、能力素质），4个一级指标（4个评价群体：学生、班委、辅导员、班主任）确定相应指标权重结；用实例对商洛学院数学与计算机应用学院某班学生进行了综合考评。用直觉模糊满意度计算模型的直觉模糊合成运算自然地将初级评价结果合成高级评价结果；将定性与定量的方法结合起来对学生综合考评,科学公正且自动化程度高。弥补了传统学生综合考评费时费力,难以保证客观性和公正性的缺陷。

[1]Atanassov K T.Intuitionistie fuzzy sets[J].Fuzzy Sets and Systems,1986,20(1)：87,96.

[2]陈东锋,雷英杰,田 野.基于直觉模糊等价关系的聚类算法[J].空军工程大学学报,2007,8(1)：63-65.

[3]赵克勤.直觉模糊直觉模糊不确定性的描述和处理[J].信息与控制,1995(3)：162-166.

[4]蔡 茹,雷英杰,申晓勇,等.基于直觉模糊等价相异矩阵的聚类方法[J].计算机应用,2009,29(1)：1233-128.

[5]任 平.优化理论中的令人满意准则[J].模糊数学,1983, 56(4)：111-112.

[6]Hopfield J J，Tand D W.Neural computation of decision in optimization problems[J].Biologieal Cybemeties, 1985,52：141-152.

[7]张 洁,郭 萌,鱼先锋.基于直觉模糊的大学生满意度研究[J].商洛学院学报,2013,27(6)：37-40.

[8]赵明宇,孙立军.基于归纳式学习法的通勤交通满意度指标研究[J].同济大学学报,2011,39(9)：1303-1308.

[9]Liu H W,Wang G J.Multi-criteria decision-making methods based on intuitionistic fuzzy sets[J].European Journal of Operational Research,2007,179：220-233.

[10]鱼先锋,李永明.基于直觉模糊的满意度计算模型[J].计算机科学,2013,40(1)：266-270.

（责任编辑：李堆淑）

Multistage Student Com prehensive Evaluation Based on the Satisfaction Degree of Intuitionistic Fuzzy Model

YU Xian-feng
(College of Mathematics and Computer Application，Shangluo University，Shangluo 726000，Shaanxi)

On the one hand,the result of student comprehensive evaluation shows student management and teaching levels of a college.On the other hand,the result shows different student's comprehensive performance advantages or disadvantages.Based on the satisfaction degree of intuitionistic fuzzy model(IFSD)4 levels evaluation index system and weight is determined,combining the data of one class of Shangluo University,an example of multistage student comprehensive evaluation is done.Integration of qualitative and quantitative methods for student comprehensive evaluation is scientific and fair.The evaluation result shows that the model is effective and practical.

IFSD;comprehensive evaluation;index system

O159

：A

：1674-0033(2014)06-0010-03

10.13440/j.slxy.1674-0033.2014.06.004

2014-05-16

商洛学院科研基金项目（12SKY009）

鱼先锋，男，陕西商州人，硕士，讲师