一种陀螺稳定平台自适应模糊-PID复合控制方法

朱倚娴，陆 源，许江宁，程向红

（1.东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2.海军工程大学 电气与信息工程学院，武汉 430033）

一种陀螺稳定平台自适应模糊-PID复合控制方法

朱倚娴1，陆 源1，许江宁2，程向红1

（1.东南大学 仪器科学与工程学院 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2.海军工程大学 电气与信息工程学院，武汉 430033）

机械摩擦、器件工作饱和区等不确定因素会导致陀螺稳定平台系统参数的波动和非线性特性，为解决非线性因素对稳定平台控制系统性能的影响，提出了一种自适应模糊-PID复合控制方法。引入自适应因子δ实现模糊控制和PID控制的复合，误差较大时增强模糊控制的作用以加快系统响应，误差较小时增强PID控制的作用以实现无静差调节。采用自调整量化因子ker(er)、kec(ec)实现基本论域的在线调整，提高了模糊控制器的灵敏度。仿真结果表明，在干扰冲击和短时常值干扰情况下，自适应模糊-PID复合控制与常规模糊控制相比，抗干扰能力显著增强，平台稳定精度提高0.4′左右。

陀螺稳定平台；模糊控制；PID；自调整量化因子；复合控制

准确测量地球各点的重力加速度值，对我国的国防建设、经济建设和科学发展有着十分重要的意义。舰载/机载重力仪安装在陀螺稳定平台的台体上，当台体由于载体晃动偏离水平位置时，惯性测量单元(IMU)敏感到变化的角速度和姿态角，误差量被输入控制器，控制器输出相应的控制电压驱动电机工作，从而带动台体转动，使其保持水平，为重力仪提供稳定的测量基准面。因此，提高陀螺稳定平台的水平稳定精度是提高重力测量系统测量精度的关键之一。

随着现代控制理论的发展，越来越多的现代控制算法被提出用于伺服稳定系统的控制。文献[1]将神经网络用于速度环的控制，有利于提高低速伺服下的稳定性能。文献[2]为适应系统模型的非精确性，采用模糊控制器实现视轴稳定，但此类单一控制策略存在可靠性差的缺陷。本文在分析双轴陀螺稳定平台隔离载体运动原理的基础上，提出自适应模糊-PID复合控制，将实时性好的PID控制和鲁棒性强的模糊控制相结合，在有效处理系统非线性特性的同时，增强了控制的可靠性。文献[3]采用阈值切换法来实现复合控制，这样的频繁切换可能导致被控对象抖动，本文引入自适应因子实现复合控制，在线调整两种控制的强度系数，提高了控制的平稳性。此外，采用自调整量化因子实现论域的在线调整[4]，增加了模糊控制器的灵敏度和稳定性。

通过仿真，验证了本文所提控制策略的有效性。

1 系统描述

1.1 系统结构

陀螺稳定平台采用双轴环架结构，如图1所示。外框为横滚环，通过支撑轴y与载体连接，内框为俯仰环，通过支撑轴x与外框连接。重力仪及惯性测量单元安装在内框的几何中心位置。IMU主要由光纤陀螺和加速度计构成，能够敏感平台的惯性速率，输出平台姿态、旋转角速度等。Mf、Mr为力矩电机，分别驱动内框、外框绕支撑轴x、y转动。

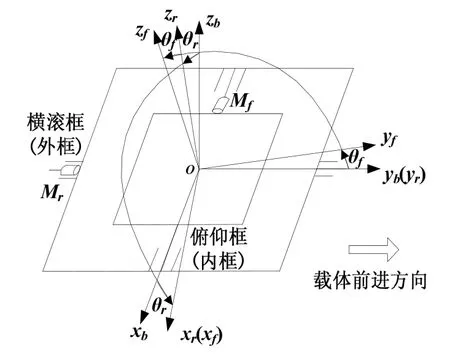
图1 陀螺稳定平台结构示意图Fig.1 Structure of gyro stabilized platform

定义坐标系如下：

① 地理坐标系n：xn、yn、zn分别指向载体所在地的东、北、天方向；

② 载体坐标系b：与载体固连，xb、yb、zb分别指向载体的右、前、上方向；

③ 外框（横滚框）坐标系r：与横滚环固连，yr轴沿横滚环轴，与yb轴指向相同，r系相对b系只能绕yb轴旋转，产生横滚环角θr；

④ 内框（俯仰框）坐标系f：与俯仰环固连，xf轴沿俯仰环轴，与xr轴指向相同，f系相对r系只能绕xr轴旋转，产生俯仰环角θf。

1.2 隔离载体运动原理

载体运动时，由于摩擦和几何约束的作用，内框会产生晃动，从而与当地水平面不重合。设为载体坐标系相对地理坐标系的角速度，fθ˙、rθ˙分别为俯仰和横滚稳定回路电机驱动产生的补偿角速度。根据环架间的坐标变换，可得横滚环相对地理坐标系的角速度：

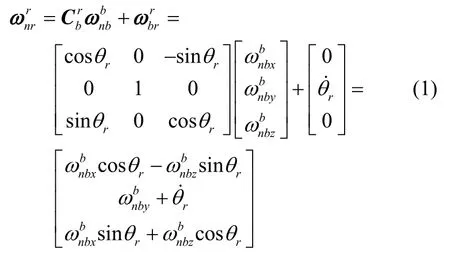
进一步，可得俯仰环相对地理坐标系的角速度：

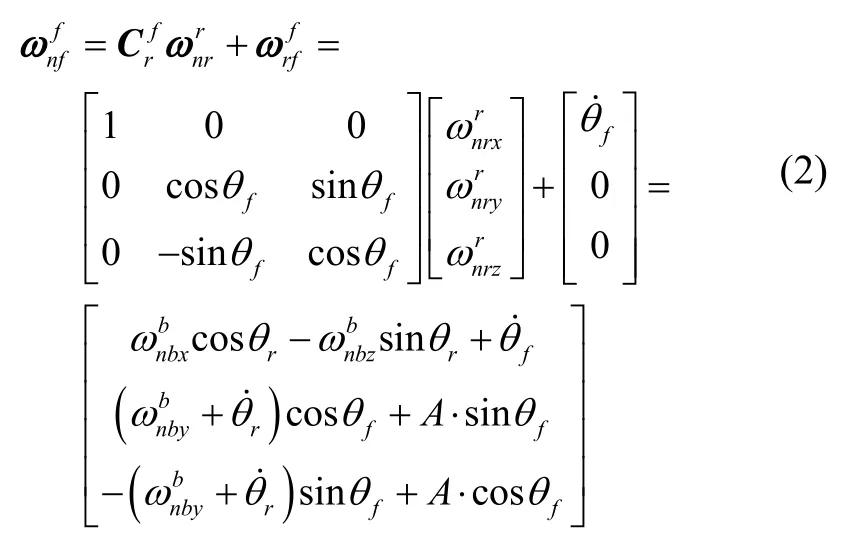
为使装载重力仪的内框始终保持在水平位置，则要求平台初始扶正后，内框相对地理坐标系的角速度为0，即满足：

联立式(2)和(3)可得两电机驱动各自负载产生的角速度需满足：

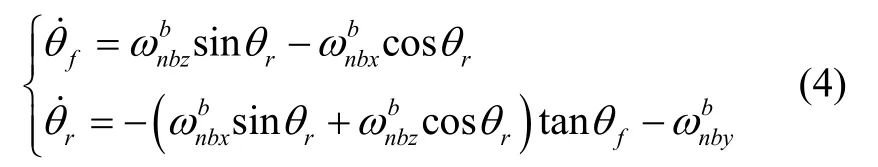
当控制结果满足式(4)时，内框将隔离载体运动产生的角速度，保持水平。

图2 俯仰轴伺服回路控制框图Fig.2 Diagram of pitch axis servo loop

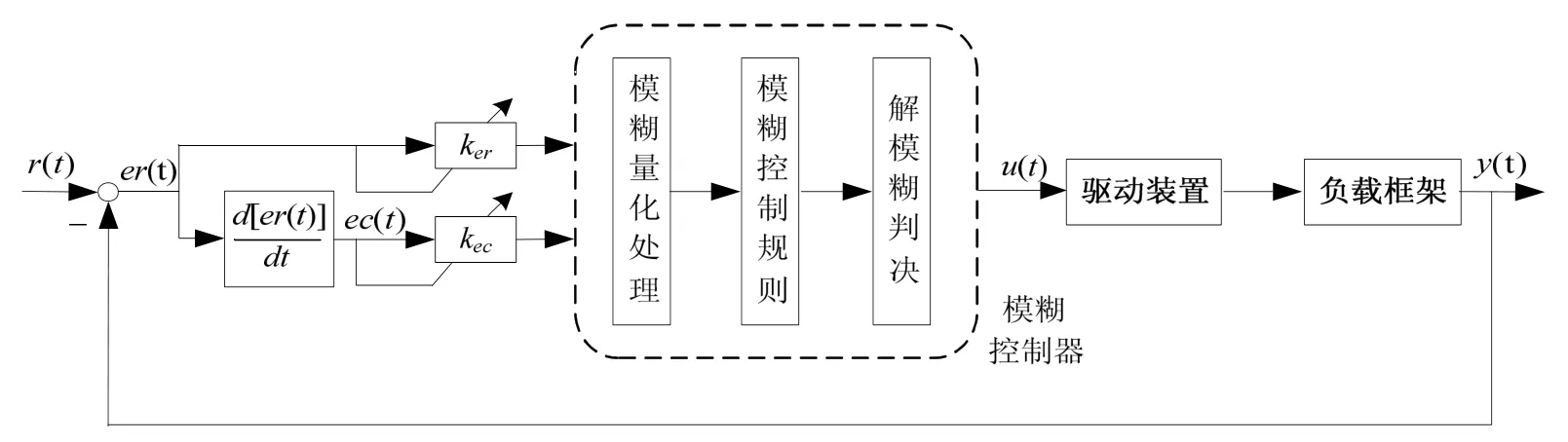
图3 量化因子自调整的模糊控制框图Fig.3 Diagram of fuzzy control with self-adjusting quantitative factors

1.3 控制框图

由于内外框架的控制回路结构基本相同，现以俯仰框为例，介绍单轴控制结构。图2为俯仰轴伺服回路控制框图，其中俯仰角P为台体相对于地理坐标系绕xn轴旋转的角度。采用位置环和稳定环共同控制的双环控制结构。稳定回路由光纤陀螺测得的角速度反馈，该回路加快了系统响应速度，及时克服外在干扰；位置回路由解算得到的台体姿态反馈，该回路实现了平台对当地水平面的准确跟踪。

2 自适应模糊-PID复合控制

2.1 模糊控制器

陀螺稳定平台是一个具有强非线性的机电控制系统[5]。机械谐振、摩擦、随机干扰、轴间力矩耦合、陀螺漂移等不确定干扰因素使得平台系统的准确数学模型无法确定。模糊控制是一种基于模糊规则的控制[6-7]，在设计过程中不需要建立被控对象的准确数学模型，因此适用于非线性稳定平台的控制。

常规模糊控制的论域是既定的，不变的。如果论域范围选取过大，则输入变量较小时，模糊控制器的调节显得比较粗糙，甚至导致系统在零点附近出现振荡；如果论域范围选取过小，则输入变量易超出论域范围，从而导致系统失控。通过量化因子的自调整能够有效地解决这个问题。量化因子根据输入变量的大小进行在线调节，可以有效增强模糊控制器的灵敏度。

图3为量化因子自调整的模糊控制框图。此处用于陀螺稳定平台的模糊控制器采用双输入单输出的结构，输入语言变量为误差ER和误差变化率EC，输出语言变量为控制电压U。

① 自调整模糊量化处理

输入、输出变量均采用模糊子集{NB，NM，NS，Z，PS，PM，PB}，分别表示负大、负中、负小、零、正小、正中、正大。工程应用中，考虑计算量及算法简便性的要求，选择对称、均匀分布、全交迭的三角形隶属函数。

设输入变量误差er和误差变化率ec的基本论域（即实际变化范围）分别为[ermin，ermax]、[ecmin，ecmax]。将输入模糊论域归一化为[-1，1]，则正规化公式为：

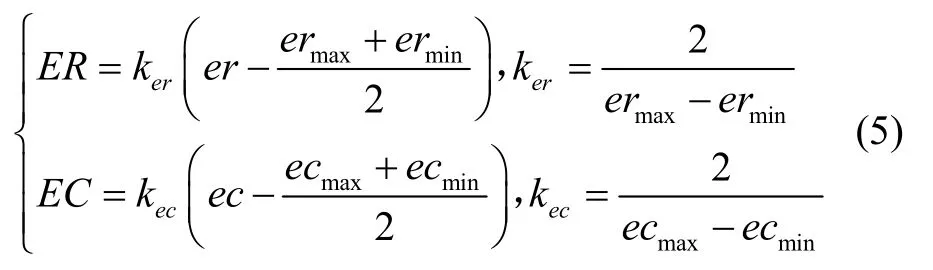
式中，ker、kec为输入变量量化因子。

自调整量化因子的表达式为：

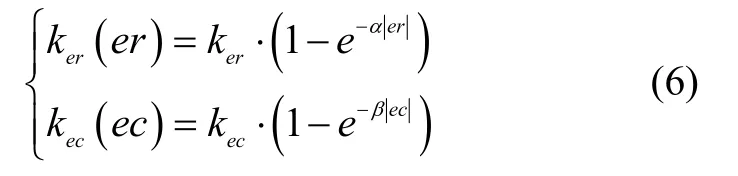
式中，α＞0，β＞0。以误差er为例，分析自调整因子的调节原理。当误差er较大时，ker(er)较大，相当于基本论域缩小，此时控制作用增强，加快响应速度；当误差er较小时，ker(er)较小，相当于基本论域扩大，此时控制作用减弱，避免超调。

② 模糊控制规则

采用“IfERiandECithenUi”形式的模糊控制语句，根据稳定平台工作特征及一些控制经验，确定模糊控制规则表[8]，共有7×7=49条规则。

模糊控制器采用Mamdani最大-最小推理法则：

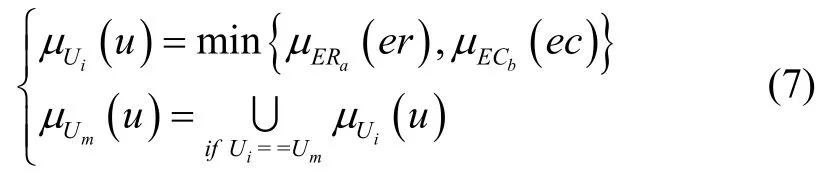
式中，a=NB，...PB，b=NB，...PB，m=NB，...PB，i=1，...，49，为第i条规则的激励强度，为属于相应模糊子集的隶属度。

③ 解模糊判决

重心法理论上是最合理的解模糊判决方法，但计算比较复杂，因此选用系数加权平均法来解模糊化，则模糊控制的输出电压U为：

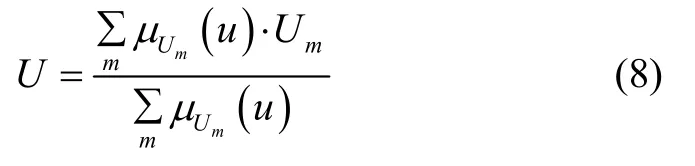
式中，Um为模糊子集对应的中心论域值。

2.2 复合控制

模糊控制运用模糊推理，实现对控制电压的最佳调整，因而具有较强的鲁棒性，适用于非线性系统，但一般情况下其稳态控制精度不理想。而PID控制在适当的参数设置下，可以具有较好的稳定精度，并且其算法简单、实时性好、易于实现。为达到系统高精度和高稳定性的要求，将PID控制和模糊控制有机结合起来。当误差较大时，增强模糊控制的作用来加快系统响应速度，同时提高系统抗干扰能力；当误差较小时，增强PID控制的作用来实现无稳态误差的调节目标。复合控制原理图如图4所示。

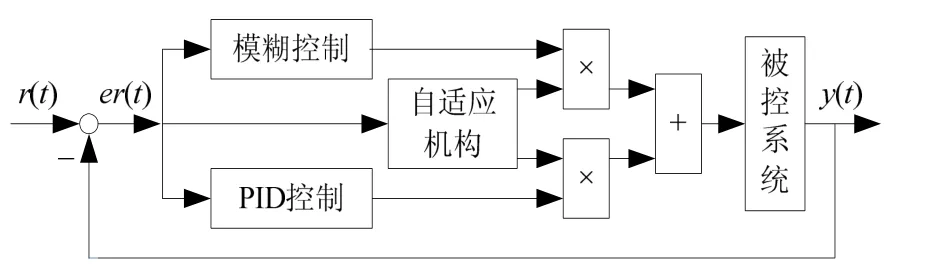
图4 复合控制原理图Fig.4 Diagram of principle of hybrid control

自适应机构不断在线调节模糊控制和PID控制的复合度。这种方法可以避免机械切换导致的台体抖动。采用自适应因子δ形如：

式中，er为误差，k为正常数。

符合控制规则的分配为：以δ作为常规PID控制的强度系数；以1-δ作为模糊控制的强度系数。因此，复合控制最终输出电压U为：

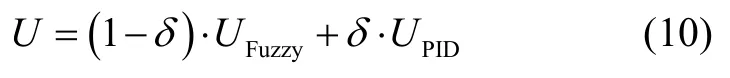
式中，UFuzzy为模糊控制的输出电压，UPID为常规PID控制的输出电压。

现讨论常数k的取值对复合控制的影响。设误差er取值范围为[-2，2]，k值取(0，2]中的数，则自适应因子δ的变化如图5所示。当k的取值小于0.35时，δ恒大于0.5，此时PID控制在复合控制中始终起主导作用；当k的取值大于0.35时，随着k值的增大，模糊控制在误差较大时所起的作用越来越大。

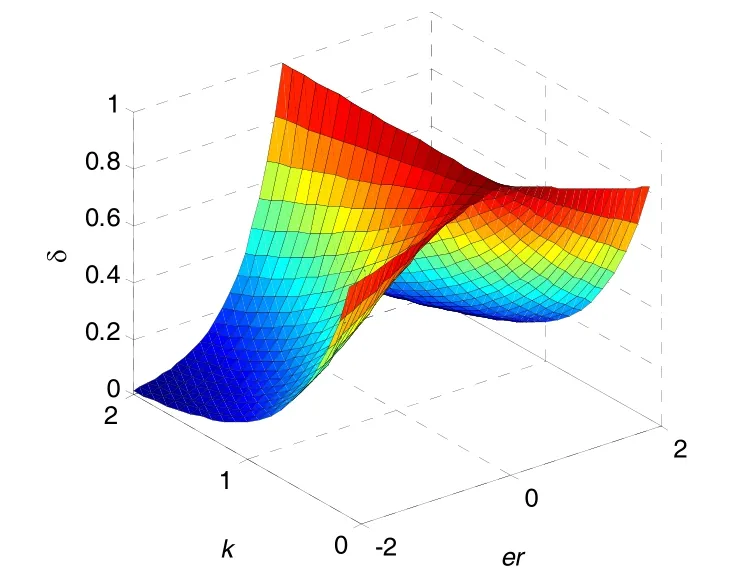
图5 自适应因子δ变化图Fig.5 The change of adaptive factor δ

3 仿真及分析

仿真条件设置为陀螺常值漂移0.03 (°)/h，电机峰值扭矩40 N·m，伺服采样频率1 kHz。载体运动采用双正弦波叠加晃动，幅值分别为25°和20°，频率分别为0.125 Hz和0.1 Hz，相位差为60°。选取误差er的论域为[-10，10]rad/s，误差变化率ec的论域为[-1000，1000]rad/s2，控制电压u的论域为[-10，10]V。经调试，自调整量化因子参数取α=2.5，β=2，自适应因子参数取k=0.25。

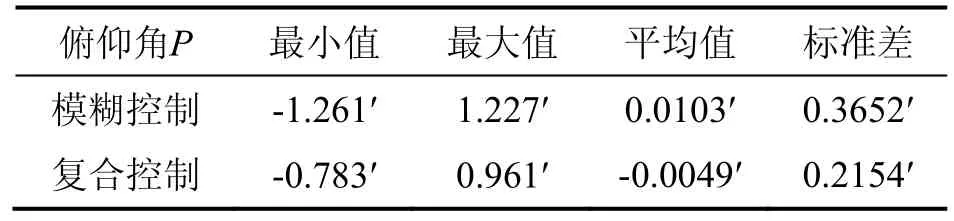
表1 仿真数据Tab.1 Simulation data

为检验自适应模糊-PID复合控制下平台隔离载体晃动的有效性，仿真时间18 s，得到图6所示的不同控制策略下的俯仰方向平台稳定精度。表1列出了两种控制结果的参数对比：常规模糊控制的稳定精度在1.2′左右；复合控制的稳定精度在 0.8′左右。可见，复合控制较常规模糊控制下平台的稳定精度提高约0.4′。

为检验自适应模糊-PID复合控制下陀螺稳定平台的抗扰动能力，进行下列两组仿真，仿真时间均为18 s：①在第8 s处施加幅值10 N·m、持续时间1 s的脉冲干扰力矩，得到图7所示结果；常规模糊控制下平台在干扰处的稳定精度为 2.655′，复合控制下平台在干扰处的稳定精度为0.976′。②在第8 s处施加幅值10 N·m的阶跃干扰力矩，得到图8所示结果；常规模糊控制在仿真时间内未能及时收敛，而复合控制在施加干扰后的3 s内恢复到正常稳定精度。综上，复合控制较常规模糊控制下平台的抗干扰能力显著增强。

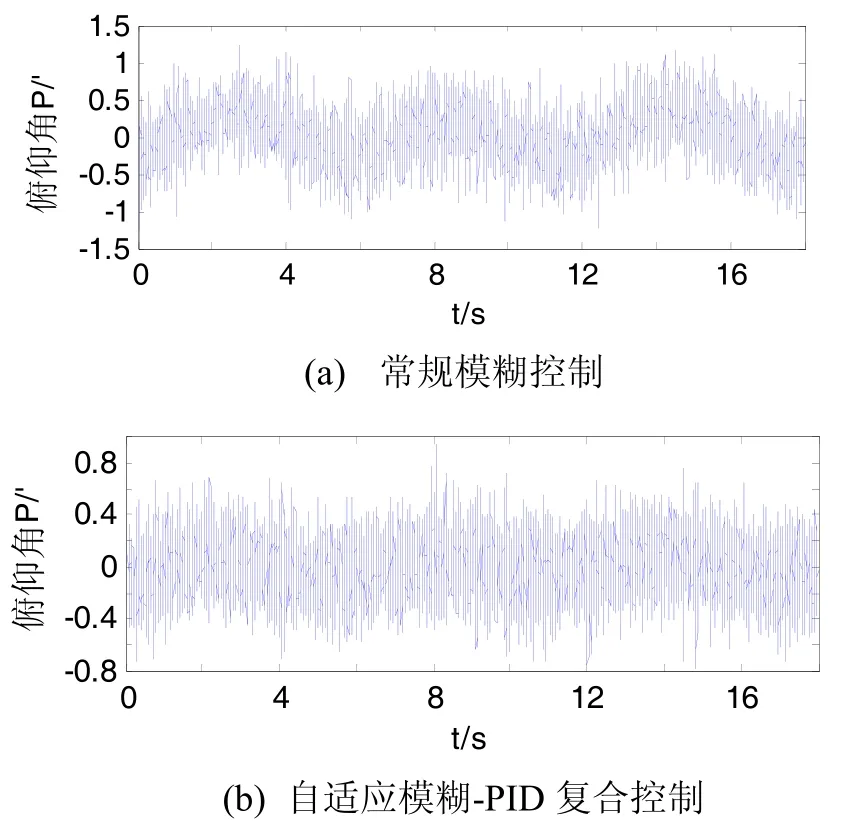
图6 俯仰方向平台稳定精度Fig.6 Stable precision of platform in pitch

图7 脉冲干扰下的俯仰方向稳定精度Fig.7 Stable precision in pitch under impulse inference

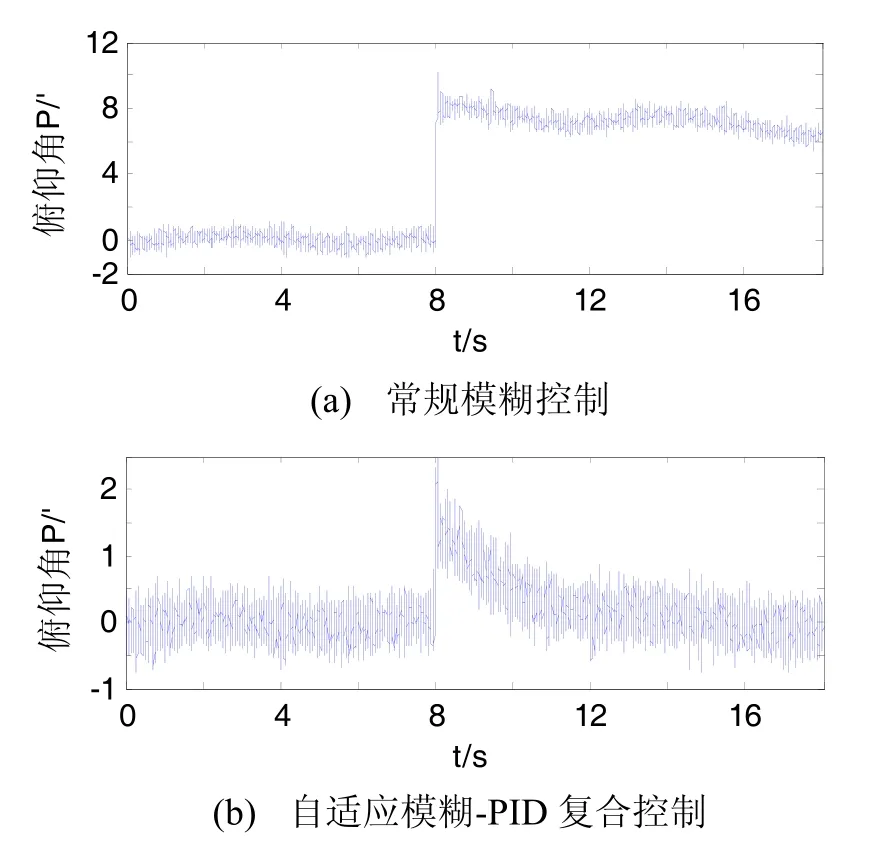
图8 阶跃干扰下的俯仰方向稳定精度Fig.8 Stable precision in pitch under step inference

3 结 论

本文分析了双轴重力仪陀螺稳定平台隔离载体晃动的原理，并针对该强非线性系统，提出了自适应模糊-PID复合控制器。运用自调整量化因子ker(er)、kec(ec)实现论域的在线调整，从而提高模糊控制器的灵敏度。引入自适应因子δ根据误差信号在线调整PID控制和模糊控制的复合度，以使系统获得更好的动静态特性，并给出了自适应因子相关参数的选取规则。仿真结果表明与常规模糊控制相比，自适应模糊-PID复合控制使陀螺稳定平台抗干扰能力显著增强，同时提高了其稳定精度，为实现高精度重力测量平台系统提供了一种新的途径。

（References）：

[1]Ma Shiqiang，Ding Yuan，Li Nian-feng.Application of neural network in the velocity loop of a gyro-stabilized platform[C]//IEEE Transportation，Mechanical，and Electrical Engineering.2011:564-567.

[2]Jark M，Marathe R，Babu H.Fuzzy controller for line-of-sight stabilization systems[J].Optical Engineering，2004，43(6):1394-1400.

[3]郑勇，李宏，张群，丁宇汉.基于模糊PI混合控制的自主水下航行器推进系统[J].测控技术，2011，3(11):65-67.ZHENG Yong，LI Hong，ZHANG Qun，DING Yu-han.Propulsion system of autonomous underwater vehicle based on fuzzy PI mixed control[J].Measurement &Control Technology，2011，3(11):65-67.

[4]文生平，赵国平，蔡康雄.一种变论域模糊控制自适应算法[J].控制理论与应用，2009，26(3)：265-268.WEN Sheng-ping，ZHAO Guo-ping，CAI Kang-xiong.A fuzzy-control adaptive algorithm with variable domain[J].Control Theory &Applications，2009，26(3):265-268.

[5]Wei Ji，Qi Li，Bo Xu.Adaptive fuzzy PID composite control with hysteresis-band switching for line of sight stabilization servo system[J].Aerospace Science and Technology，2011，15(1):25-32.

[6]Cai Kai-Yuan，Zhang Lei.Fuzzy reasoning as a control problem[J].Fuzzy Systems，2007，16(3):600-614.

[7]Li Yingfang，Qin Keyun，He Xingxing.Robustness of fuzzy connectives and fuzzy reasoning[J].Fuzzy Sets and Systems，2013，225(16):93-105.

[8]李景森，奚碚华，付中泽，宋超.模糊-线性双模控制在平台稳定回路中的应用[J].中国惯性技术学报，2008，16(4)：390-395.LI Jing-sen，XI Bei-hua，FU Zhong-ze，SONG Chao.Application of fuzzy-linear dual-mode control in platform stabilization loop[J].Journal of Chinese Inertial Technology，2008，16(4):390-395.

Adaptive fuzzy-PID hybrid control method of gyro stabilized platform

ZHU Yi-xian1，LU Yuan1，XU Jiang-ning2，CHENG Xiang-hong1
(1.School of Instrument Science &Engineering，Key Laboratory of Micro-inertial Instrument and Advanced Navigation Technology，Ministry of Education，Southeast University，Nanjing 210096，China;2.Electrical Engineering and Information Engineering College，Naval University of Engineering，Wuhan 430033，China)

System parameters of gyro stabilized platform are unpredictable because of the uncertainty factors such as mechanical friction，the saturation characteristic of the driver module，etc.To suppress the error caused by the nonlinear characteristics，an adaptive fuzzy-PID hybrid control method is proposed.The adaptive factorδis set up to combine fuzzy control and PID control.When the large attitude error of the platform is detected，the effect of fuzzy control is enhanced to decrease the system response time.And the conventional PID control effect is enhanced to eliminate the static error when the attitude error is small.Self-adjusting quantitative factorsker(er) andkec(ec) are proposed to adjust the basic domain of the fuzzy controller online，which improves the sensitivity of the control loop.The simulation results show that，in both cases of pulse and step interference，the adaptive fuzzy-PID hybrid control can improve the accuracy of platform attitude about 0.4 arc min and enhance its capability of anti-jamming compared to ordinary fuzzy control.

gyro stabilized platform;fuzzy control;PID;self-adjusting quantization factor;hybrid control

TP273

A

1005-6734(2014)03-0317-05

10.13695/j.cnki.12-1222/o3.2014.03.008

2013-12-20；

2014-04-11

国家重大仪器项目（2011YQ2004502）

朱倚娴（1989—），女，博士研究生，专业为导航、制导与控制。E-mail：zhuyixian911@163.com

联 系 人：程向红（1963—），女，教授，博士生导师。E-mail：xhcheng@seu.edu.cn