激光陀螺组合体自主测量船体角变形的最优估计法
杨云涛,王省书,吴 伟,黄宗升
(国防科学技术大学 光电科学与工程学院,长沙 410073)
激光陀螺组合体自主测量船体角变形的最优估计法
杨云涛,王省书,吴 伟,黄宗升
(国防科学技术大学 光电科学与工程学院,长沙 410073)
根据激光陀螺组合体测量的角增量计算得到的惯性姿态匹配测量方程,结合动态变形模型和静态变形模型,构建了船体角变形测量的最优滤波器,实现了角变形的最优估计。该方法将角变形和激光陀螺的随机漂移误差近似为平稳随机过程并分别构建滤波器,静态变形建模为白噪声驱动的一阶随机游走过程,动态变形建模为二阶马尔可夫平稳随机过程。通过角速度匹配测量方程进行了角变形的观测性分析得知:动态变形的估计精度与激光陀螺的测量精度相当,静态变形的估计精度依赖于船体摇摆频率和幅度,因此最优估计法的误差主要为静态角变形模型的估计误差。仿真结果表明,通过设置合适的静态角变形模型参数,该最优估计法测量角变形的误差小于10″。
船体角变形测量,激光陀螺组合体,静态角变形模型,最优估计
现代舰船都配备有大量的雷达监测设备、跟踪测量设备、武器发射设备、光学跟瞄设备和其它带有基准坐标系的精密设备等[1-3]。各种设备之间需要有统一的基准坐标系才能协同工作,发挥最大的作战效能[4-5]。基准坐标系的统一其实质就是角变形的测量,角变形的测量方法有很多[1],如光学测量法、GPS测量法和姿态基准测量法。其中光学测量法因需要有通视条件且灵活性较差而限制了其应用;GPS测量法也需要有通视条件且易被敌方捕获;姿态基准测量法[9-10]不依赖于通视条件,且具有测量的灵活性,但由于该测量法的自主测量精度不高,需要外部阻尼组合最优滤波才能得到最优解,因此并不是理想的自主测量。
惯性基准测量法充分利用了激光陀螺对惯性空间旋转角速度的敏感原理,比较两套激光陀螺组合体(Laser Gyro Unit,LGU)测量的惯性空间角速度进行两个基准坐标系间的角度测量。Mochalov[6-7]研究了利用 LGU测量船体角变形,结合角速度匹配测量方程和动态变形的二阶马尔可夫模型构建了角变形的最优滤波器,实现了角变形的自主测量。但是由于激光陀螺输出为角增量,信噪比低,角速度匹配的测量方程易受测量噪声的干扰。文献[8-10]在文献[6-7]的基础上,利用两 LGU的陀螺角增量进行姿态计算,得到了机体坐标系下的惯性姿态匹配测量方程并构建了最优滤波器。该方法相比角速度匹配测量的方法具有测量信噪比高的优点,估计效果大大提高。
本文基于惯性姿态匹配的测量方程,考虑到激光陀螺的随机漂移误差和非平稳的静态角变形的影响,将从理论上详细分析直接测量法与最优估计法的优缺点和适用条件,并对最优估计法进行仿真验证。
1 惯性姿态匹配的测量方程
LGU自主测量船体角变形的原理示意图如图1所示。
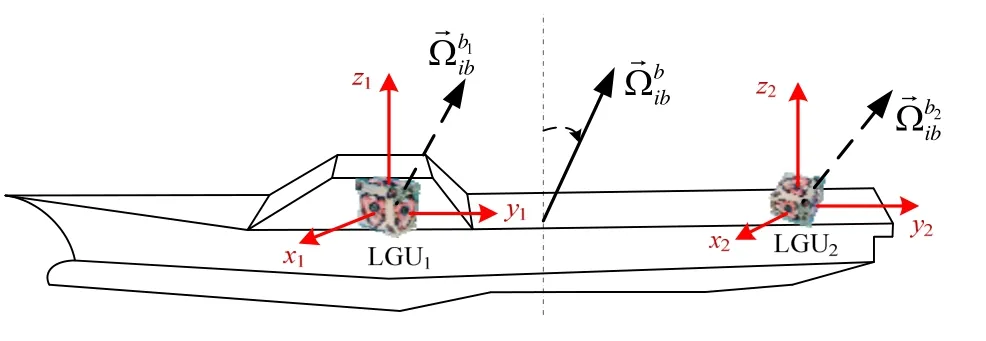
图1 LGU测量船体角变形的原理示意图Fig.1 Schematic of ship angular deformation measurement by LGU
根据文献[7],小角度形变近似条件下的姿态匹配测量方程为

式中姿态误差微分方程在初始载体坐标系的表示形式为:


2 激光陀螺随机漂移误差的影响
激光陀螺输出为单位采样时间的角增量,其中包含有测量误差,主要由随机零偏和随机游走两部分组成。随机游走可认为是均值为零,方差发散的随机过程,因此在角变形测量中随机零偏的影响最大。
已知 LGU测量船体角变形的原理是基于角速度映射机理推导得来的[6],即:
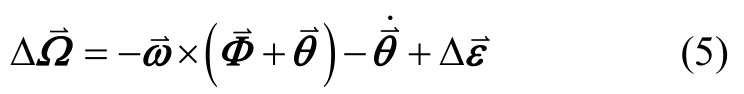
3 最优估计法
激光陀螺组合体测量船体角变形的最优估计法应用研究起始于 Mochalov等人的工作,它约束了动态变形的变化规律服从二阶马尔可夫平稳随机过程,并构建了 Kalman最优滤波器。下面将根据惯性姿态匹配的测量方程,分析直接测量法的缺点,并引出最优估计法的设计思路和可行性,给出适用条件。
3.1 直接测量法的缺点
激光陀螺测量船体角变形的直观思路就是直接测量法,即直接利用测量方程进行时间更新计算角变形。将式(1)进行变换可得测量公式为:

正因为激光陀螺的测量误差具有随机零偏特性,故在实际应用中需要加以约束。
3.2 角变形的最优滤波器
直接测量法受激光陀螺的随机零偏影响较大,故需要对其加以约束。可建模为

其中,白噪声驱动幅度是一个很小的量。由式(7)可知,激光陀螺的随机零偏是一个随机的常值。
静态变形可建模为:

式(8)与式(7)的区别在于驱动幅度的大小不同,后者根据实际情况会产生变化,需要在线辨识。
Mochalov等人的方法中假定了静态变形是稳定常值,等效为将式(8)的驱动噪声幅度设置为零,这样做的好处在于模型是确定性过程,但缺点在于它不能准确描述静态变形的缓慢变化。由于静态变形的缓变不是各态历经且平稳的,因此可认为是一种非平稳过程。已知静态变形的缓慢变化是有界的,因此可利用非平稳的单位根过程来描述,即式(8)。从这个意义上来说,式(8)是合理的。
得到了静态变形的约束方程,还缺少动态变形的约束方程。最直观的思路就是依据测量方程式(6)进行模型辨识。最常见的模型辨识就是AR模型[11-14],由于AR平稳过程可以采用并联型滤波结构,即分解成多个一、二阶马尔可夫平稳过程的和,各个子模型间是相互独立的,模型参数的求解是无耦合的,因此最适于最优滤波。Mochalov采用的二阶马尔可夫模型能够准确求出模型描述的动态变形,单个二阶马尔可夫模型是单高斯分布,多个即为多高斯分布,可根据实际情况扩充动态变形的模型个数。动态变形的二阶马尔可夫模型为
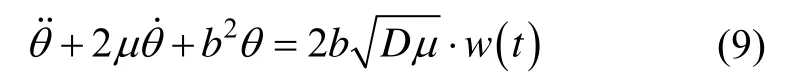
式中,b2=μ2+λ2,μ为动态变形的阻尼系数,λ为动态形变的支配频率,D为动态变形的功率谱密度幅值。
因此,式(7)~(9)构成了最优滤波器的状态约束方程,式(6)为测量方程,它们共同构成了角变形测量的最优滤波器,可依据 Kalman最优估计算法进行角变形的求解。
3.3 最优估计法的适用条件
构建了角变形测量的最优滤波器,需要对此滤波过程进行信号分析。由于最优估计法其实质是模型信息和测量信息的最优融合,因此测量条件决定了最优估计法的适用条件。
对式(6)进行线性方程解的相对误差分析,即
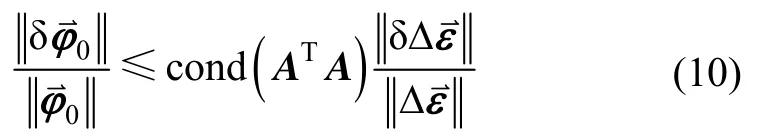
A A的大小。又因为cond(ATA)< 1,因此初始角变形误差的上限不是一个稳定值,有时会出现误差发散的可能。
动态变形相对误差的条件数显然为 1,故动态变形误差相当于随机零偏差值的量级(<0.01 (°)/h),可以忽略不计。
由于静态变形与初始角变形是同一数值,因此初始角变形的估计精度直接决定着角变形的估计精度。初始角变形的条件数总是小于 1,说明了静态变形的估计精度是主要限制因素。只要陀螺的随机零偏不可知,静态变形就总是受到观测条件的约束而使得角变形的估计精度不稳定,估计方差不收敛。当观测条件数较小时,静态变形估计精度就会变差。从这个意义上来说,最优估计法的优势在于观测的更新,角变形的估计精度直接决定于观测的更新效果。
船体作适当的机动航行来变化摇摆姿态可以改善角变形的估计效果。
观察测量方程式(6)可知,动态变形模型辨识时易受到初始角变形的观测量的影响,有可能两者的支配频率是重叠的,能够区分两者的唯一参数只有驱动幅度,因此辨识时驱动幅度也不是准确的。考虑到动态变形近似为一个平稳随机过程,方差是一个定值,此时最优估计后初始角变形误差的均值为一个常值偏置[8]。当船体作机动航行时,船体摇摆频率[20]受船速的影响发生变化,动态变形依然保持平稳性参数不变,此时动态变形和初始角变形的观测量可以分离开来,角变形的估计精度提高。
4 仿真验证
4.1 仿真参数设置:
1)设置安装误差角为 0.2°、0.1°0.1°和 0.05°。
2) 动态形变角满足二阶马尔可夫随机过程,支配频率为[0.17 0.10 0.14]Hz,衰减系数为[0.11 0.14 0.15],驱动噪声为有色噪声,通过国际海浪谱 ISSC计算得到,幅度标准差为[10″ 15″ 10″]。
3)舰船以二阶马尔可夫随机过程绕航向轴、纵摇轴和横摇轴作三轴摇摆,摇摆支配频率为[0.085 0.05 0.07]Hz,同样地驱动噪声为有色噪声,通过国际海浪谱 ISSC 计算得到,幅度标准差为[2.44° 2.26°0.96°]。
4.2 结果和分析
仿真时间设置为9 h。采用最优估计法进行角变形的求解。为了验证模型在最优估计中的作用,比较静态变形模型的驱动噪声方差分别为零和非零时的估计效果。静态变形模型为式(8)。驱动噪声方差为零时的估计效果如图2所示,驱动噪声方差为适当非零值时的估计效果如图3所示。比较图2与图3可知,自主测量船体角变形的最优估计法依赖于角变形模型,特别是静态变形模型的驱动噪声方差决定了估计效果。仿真结果表明角变形的最优估计精度可达10″。
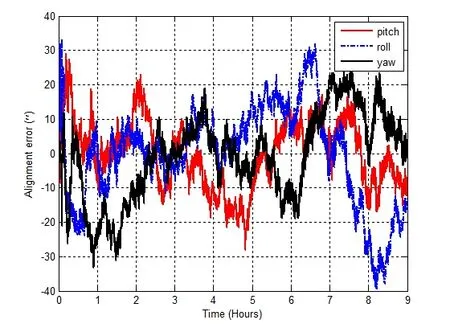
图2 静态变形模型驱动噪声方差为零时的估计误差Fig.2 Estimation error when variance of static deformation model is zero

图3 静态变形模型驱动噪声幅度为非零值时的估计误差Fig.3 Estimation error when variance of static deformation model is non-zero
5 结 论
基于惯性姿态匹配测量方程,比较了直接测量法和最优估计法的测量精度。考虑到激光陀螺随机漂移误差的影响,分析了直接测量法会导致角变形的测量误差累积而发散。
通过将静态变形和陀螺的随机零偏建模为单位根随机过程模型,动态变形建模为二阶高斯马尔可夫随机过程型模型,构建了角变形的最优估计滤波器。基于条件数的判断,得出静态变形的估计精度比动态变形低,且受到陀螺的随机零偏影响,在观测条件变化剧烈时静态变形的估计精度会提高。静态变形模型参数需要通过在线辨识得到。
(References):
[1]朱昀炤,汪顺亭,缪玲娟,葛远声.船体变形测量技术综述[J].船舶工程,2007,29(6):58-61.ZHU Yun-zhao,WANG Shun-ting,MIAO Ling-juan,GE Yuan-sheng.Review of measuring technique for ship deformation[J].Ship Engineering,2007,29(6):58-61.
[2]Mennitt S H.The effects of ship load variations and seastate on hull girder deflection and combat system alignment[D].USA:Massachusetts Institute of Technology,1990.
[3]Hutcheson L D.Ship flexure measurement[R].CA:Naval Weapon Center,Report AD A06349,1975-08.
[4]汪顺亭,汪湛清,朱昀炤,等.船体变形的监测方法及其对航向姿态信息的修正[J].中国惯性技术学报,2007,15(6):635-641.WANG Shun-ting,WANG Zhan-qing,ZHU Yun-zhao,et al.Monitoring on ship hull deformation and correction for heading &attitude information[J].Journal of Chinese Inertial Technology,2007,15(6):635-641.
[5]万德钧,刘玉峰.消减舰船变形的影响和为全舰提供高精度姿态基准[J].中国惯性技术学报,2005,13(4):77-82.WAN De-jun,LIU Yu-fen.Summary on removing influence of ship deformation and providing accurate attitude references for warship[J].Journal of Chinese Inertial Technology,2005,13(4):77-82.
[6]Mochalov A V,Kazantsev A V.Use of ring laser units for measurement of the moving object deformation[C]//Proceeding of the SPIE,2002,Vol.4680:85-92.
[7]Mochalov A V.A system for measuring deformation of large-sized objects[C]//RTO/NATO.France,1999:1-9.
[8]郑佳兴,秦石乔,王省书,等.基于姿态匹配的船体形变测量方法[J].中国惯性技术学报,2010,18(2):175-180.ZhENG Jia-xing,QIN Shi-qiao,WANG Xing-shu,et al.Attitude matching method for ship deformation measurement[J].Journal of Chinese Inertial Technology,2010,18(2):175-180.
[9]郑佳兴,秦石乔,王省书,等.考虑准静态缓变量的船体角形变测量[J].中国惯性技术学报,2011(1):6-10.ZhENG Jia-xing,QIN Shi-qiao,WANG Xing-shu,et al.Ship hull angular deformation measurement taking slowvarying quasi-static component into account[J].Journal of Chinese Inertial Technology,2011(1):6-10.
[10]郑佳兴.激光陀螺组合体船体形变测量关键技术研究[D].长沙:国防科学技术大学,2012.ZhENG Jia-xing.Research on ship angular flexure measurement based on ring laser gyroscope units[D].Changsha:National University of Defense Technology,2012.
[11]WU Wei,ChEN Sheng,QIN Shi-qiao.Online estimation of ship dynamic flexure model parameters for transfer alignment[J].IEEE Trans.on Control Systems Technology,2013,21(5):1666-1678.
[12]WU Wei,QIN Shi-qiao,CHEN Sheng.Coupling influence of ship dynamic flexure on high accuracy transfer alignment[J].Int.J.Modelling,Identification,and Control,2013,19(3):224-234.
[13]WU Wei,QIN Shi-qiao,CHEN Sheng.Determination of dynamic flexure model parameters for ship angular deformation measurement.Proc[C]//UKACC Control 2012.Cardiff,UK,2012:964-969.
[14]Kumaresan R,Tufts D.Estimating the parameters of exponentially damped sinusoids and pole-zero modeling in noise[J].IEEE Trans.Acoust,Speech Signal Processing,1982,30(6):833-840.
Optimal estimation of ship angular deformation for autonomous measurement by laser gyro unit
YANG Yun-tao,WANG Xing-shu,WU Wei,HUANG Zong-sheng
(College of Opto-electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China)
Based on the inertial attitude matching measurement equation calculated from angular increment output of a laser gyro unit(LGU),an optimal filter for implementing ship angular deformation measurement is formed with static deformation model and dynamic flexure model.In the optimal filter,by assuming that the ship angular deformation and sensor’s error of LGU are stationary random process,the static deformation is modeled as the first order random walk process with white noise,and the dynamic flexure are modeled as second order Gaussian-Markov random process.The observability analyses of angular deformation by angular rate matching equation show that the estimation error of dynamic flexure is similar to laser gyro’s error,and estimation error of static deformation is modulated by swing frequency and amplitude of ship motions.So the estimation error of static deformation is the main factor of optimal estimation in ship angular deformation measurement.The simulations are made by setting proper parameters of static deformation model,and the results show that the estimation error of angular deformation is lower than 10″ .
ship angular deformation measurement;laser gyro unit;static angular deformation model;optimal estimation
U666.1
A
1005-6734(2014)03-0284-04
10.13695/j.cnki.12-1222/o3.2014.03.002
2014-01-16;
2014-05-12
高等学校博士点专项科研基金(博导类)(20134307110023)
杨云涛(1984—),男,博士研究生,从事光电仪器与测控技术研究。E-mail:legend08fda@126.com
联 系 人:王省书(1963—),女,教授,博士生导师。E-mail: gfkdwxs@163.com

