捷联惯导系统双位置快速抗干扰对准方法
刘永红,刘明雍,谢 波
(1.西北工业大学 航海学院,西安 710072;2.航天第十六研究所,西安 710100)
捷联惯导系统双位置快速抗干扰对准方法
刘永红1,刘明雍1,谢 波2
(1.西北工业大学 航海学院,西安 710072;2.航天第十六研究所,西安 710100)
经典捷联惯导系统双位置参数辨识精对准采用水平速度作为量测值,对部分参数辨识时间较长,且收敛速度受递推计算初值影响。提出了一种利用单位时间的水平比力作为量测值的双位置快速抗干扰对准方法,并忽略误差构成的高阶项,可以将三次曲线转换为线性模型进行估计,提高了初始对准的收敛速度。双位置对准试验结果表明,双位置快速抗干扰对准方法算法计算量小,算法简单,对准速度快,抗干扰性强,对准精度高且不受递推计算初值的影响,具有较强的工程实用价值。
捷联惯导系统;参数辨识;对准;抗干扰
在捷联惯导系统初始对准工程应用中,主要有三个问题:1)高精度对准;2)快速对准;3)抗干扰对准。对于捷联惯导系统单个位置的对准来说,无论采用经典的三阶调平回路及方位罗经对准,还是采用卡尔曼滤波技术,对准精度直接受限于惯性器件的漂移大小。为了提高对准精度,常采用双位置对准法。双位置对准法可以克服惯性器件漂移对自对准精度的影响,并且能够在对准的同时进行惯性器件漂移的估计。捷联惯导系统常用的抗干扰对准方法有罗经法、Kalman滤波法和最小二乘参数辨识法等,与其它方法相比,最小二乘参数辨识法具有计算量小,实时性强,初值设置简单,收敛速度快等特点。传统的最小二乘参数辨识法以水平速度误差作为量测值,由于量测误差中包含时间的三次方项,而三次曲线在短时间内只呈现线性特性,所以方位估计和北向陀螺漂移估计所需时间仍然较长[1]。且当初始误差角较大时,由于模型非线性影响比较严重,使传统的开环最小二乘参数辨识法不适用。
文献[2]对传统的捷联惯导系统双位置最小二乘参数辨识精对准进行了详细介绍;文献[3]针对线晃动干扰环境对准,提出了将计算干扰速度的平均值列入辨识模型参数,提高了初始对准的收敛速度和对准精度,并推导了比力双重积分的参数辨识模型,有利于进一步抑制晃动干扰的影响;文献[1]直接以水平比力分量作为量测值,并忽略误差构成的高阶项,可以将三次曲线转换为线性模型进行估计,有利于缩短对准时间,实现快速对准。
本文在上述文献的基础上,提出了一种利用单位时间的水平比力作为量测值的双位置快速抗干扰对准方法。此外,为了减小失准角初值对收敛速度的影响,在每个位置对准约 30 s后对失准角进行一次闭环修正,然后再进行对准。并通过试验对新的双位置对准方法进行了验证。
1 参数辨识精对准原理

经过推导可以求得姿态误差角满足如下关系式[2]:
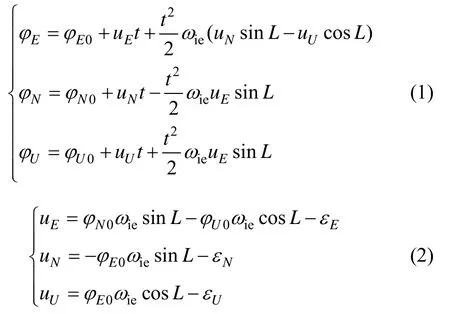
在晃动机座上,加速度计测量值包括重力加速度

式中,δA为加速度计安装误差,δKA为标度因数误差,为加速度计零偏。则有:

因此,参数辨识精对准就是利用式(1)(2)(5)通过参数辨识法来确定其初始值和等效常值漂移。
2 双位置参数辨识精对准法
2.1 经典双位置参数辨识精对准法
2.1.1 经典参数辨识法
将式(1)代入式(5),并在[0,t]内积分得速度增量:

式中,VDE和VDN是由等效干扰加速度积分获得的,没有随时间增长的趋势,而速度增量是时间的三次函数,所以对准时间的增长对抑制干扰提高辨识精度是有益的。
将式(6)改写成:
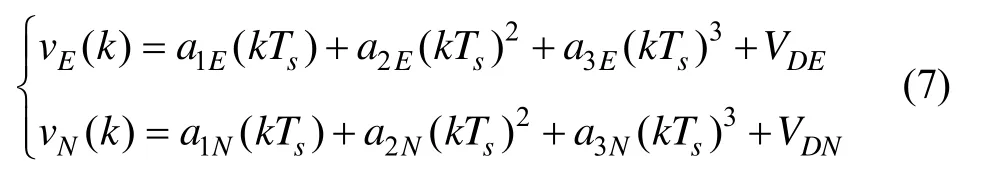
式中,Ts为采样周期;v(k)是从计算得到的,
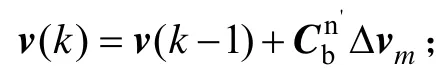
其中,Δvm为加速度计Ts时间段内的增量输出;

a1E、a2E、a3E、a1N、a2N、a3N都是常值参数。
2.1.2 经典双位置对准法
为了提高初始对准精度,需测得东向陀螺等效漂移,可以采用双位置对准法。假设正常工作位置为第二位置,且该位置捷联惯导系统的敏感轴与载体系(b系)的坐标轴平行。将捷联惯导系统绕Z轴逆时针转过 90°作为第一位置,若对准过程中载体接近水平,第一位置的北向陀螺等效漂移即为第二位置的东向陀螺等效漂移。

辨识出第一位置的北向陀螺等效漂移后,将捷联惯导系统旋转到第二位置重新进行参数辨识精对准。由于东向陀螺等效漂移已知,所以可以得到更为精确的对准航向角误差[4]。
2.2 快速双位置参数辨识精对准法
2.2.1 快速参数辨识精对准法
传统参数辨识法确定的误差方程为三次曲线,而三次曲线在短时间内只呈现线性特性,所以辨识北向陀螺等效漂移和方位误差初值所需时间较长,估计Uμ所需时间则更长。改进的参数辨识法不使用速度测量值,而直接使用等效水平比力作为量测值,并忽略失准角误差中的高阶项,可以将三次曲线转换为线性模型进行估计,从而缩短对准和测漂时间[1]。
忽略时间的高次项和Uμ,则有:
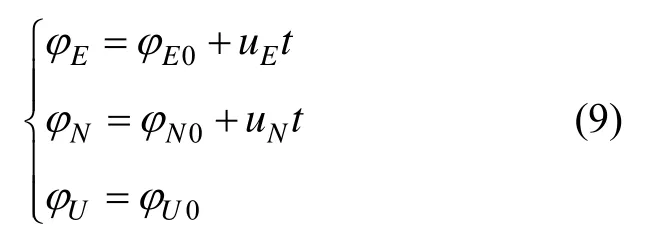
改进的参数辨识法以等效水平比力作为量测值,误差方程为[1]:
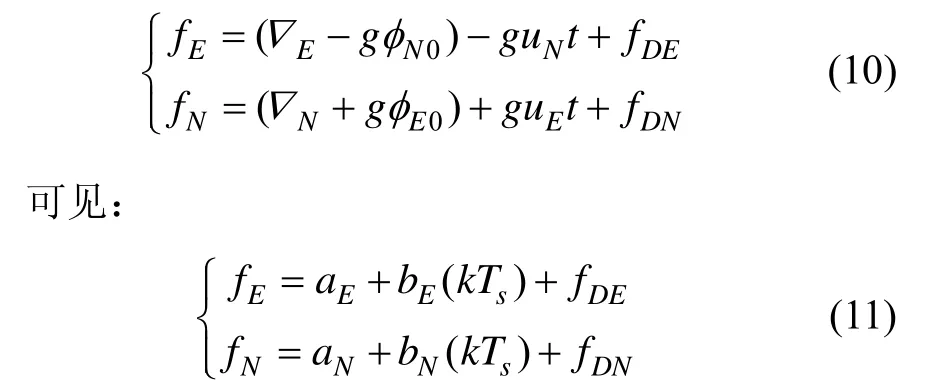
只要从式(11)中辨识出参数aE、bE、aN、bN,同样可以按照式(9)求得φE0、φN0和φU0,代入式(1),即可完成初始对准。
采用递推最小二乘算法计算如下:

式中,量测矩阵为:

2.2.2 快速双位置对准算法
经典双位置对准法需要通过式(8)估算出第一位置的北向陀螺等效漂移,其中Nμ是通过a3N计算出来,而a3N的收敛时间较缓慢,因此会影响对准的速度。快速双位置对准算法对经典双位置对准算法进行了适当改进。设正常工作位置为第二位置,该位置捷联惯导系统的敏感轴与b系的坐标轴平行。将捷联惯导系统绕Z轴逆时针转过180°作为第一位置,记作,则有:

设捷联惯导系统处于第一位置时陀螺和加速度计在导航坐标系内的等效漂移为:

捷联惯导系统处于第二位置时陀螺和加速度计在导航坐标系内的等效漂移为:

又因为对准过程中载体接近水平,近似认为:

第一位置的东向陀螺等效漂移与第二位置的东向陀螺等效漂移之和为0。设在第一位置由式(11)辨识的各参数分别为,在第二位置由式(11)辨识的各参数分别为。由于加速度计的零偏重复性误差较小、稳定性较好,所以俯仰角误差和横滚角误差可以直接用位置2的估计参数、表示为:
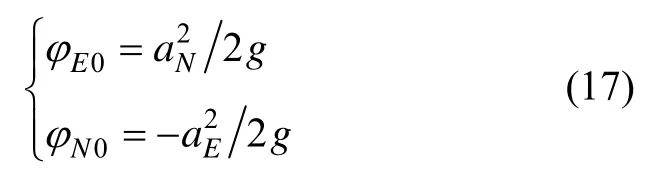
位置2的航向角误差可以表示为:

式中,Δφ为从位置1对准结束到位置2位置对准结束的期间航向角变化值。
3 误差分析
为了加快对准收敛速度,快速双位置参数辨识精对准法将式(1)进行了简化,由于忽略高次项和引入的失准角误差为[1]:
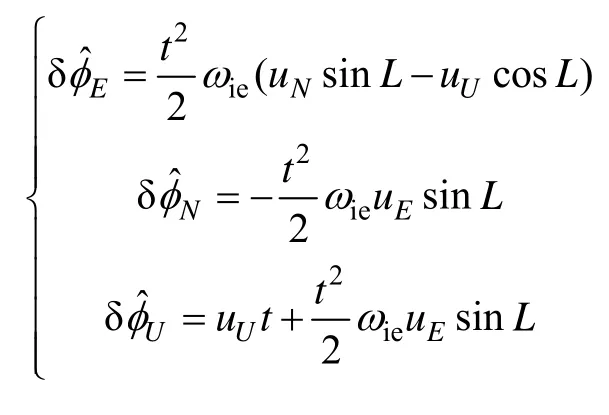
4 试验验证
试验验证在单轴转台上进行,所用的激光陀螺捷联惯导系统等效漂移约为0.03 (°)/h,加速度计等效零偏约为1×10-4g;惯性器件采样周期为5 ms。先将转台定位在第一位置(0,0,270°)上,利用转台设置频率为0.1 Hz、幅值为1.0°的振动干扰,共进行数据采集100 s,然后停止振动将转台定位在第二位置(0,0,90°)上,同样利用转台设置频率为 0.1 Hz,幅值为1.0°的振动干扰,共进行数据采集100 s。图1为试验过程中,第一次在第一位置对准期间的陀螺输出数据。

图1 陀螺输出数据Fig.1 The outputs of gyros
图2为采用经典最小二乘参数辨识法第一次在第一位置对准各参数估计曲线图。利用快速双位置参数辨识精对准法对进行对准时,具体的过程如下:30 s粗对准后,转入精对准状态,为了加快收敛速度,30 s精对准时进行一次闭环校正,然后再进行100 s精对准。
图3为采用快速双位置参数辨识精对准法第一次在第一位置经过闭环校正后再对准各参数估计曲线图。
从图2和图3可以看出采用经典最小二乘参数辨识法100 s部分参数还没有完全收敛,采用快速双位置参数辨识精对准法90 s所有参数都收敛了,所以采用快速双位置参数辨识精对准法能实现快速双位置对准。
表1是采用双位置快速抗干扰对准方法进行六次对准的结果,从表1可以看出水平姿态角的均方差均小于0.001°,航向角的均方差为0.0274°。
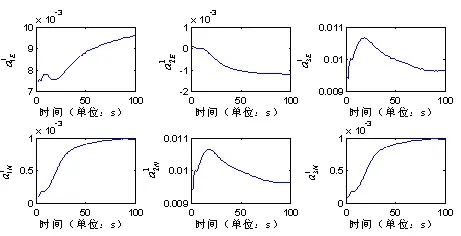
图2 采用传统最小二乘参数辨识法的参数估计曲线Fig.2 Curves of parameter estimates using traditional least-square parameter identification

图3 采用改进最小二乘参数辨识法的参数估计曲线Fig.3 Curves of parameter estimates using the improved least-square parameter identification

表1 5 min对准结果Tab.1 Result of 5 min alignment
5 结 论
经典参数辨识精对准对部分参数辨识时间较长,且收敛速度受递推计算初值影响,快速双位置参数辨识精对准法直接以比力为量测量,并忽略误差构成的高阶项,有利于缩短对准时间,实现快速对准。且这种算法不需要设置初值,计算量小,收敛速度快。因此这种对准方法具有一定的工程实用价值,较适合应用到实战环境中。
(References):
[1]付强文.捷联惯导系统快速最小二乘精对准方法[J].中国惯性技术学报,2012,20(3):278-282.FU Qiang-wen.Rapid recursive least-square fine alignment method for SINS[J].Journal of Chinese Inertial Technology,2012,20(3):278-282.
[2]严恭敏.车载自主定位定向系统研究[D].西北工业大学自动化学院,2006.YAN Gong-min.Research the vehicle autonomous position and azimuth determining system[D].Department of Automatic Control,Northwestern Polytechnical University,2006.
[3]严恭敏,翁浚,赵长山,秦永元.捷联惯导系统改进参数辨识初始对准方法[J].中国惯性技术学报,2010,18(5):523-526.YAN Gong-min,WENG Jun,ZHAO Chang-shan,QIN Yong-Yuan.Improved parameter identification method for SINS initial alignment[J].Journal of Chinese Inertial Technology,2010,18(5):523-526.
[4]白亮,秦永元,孙丽.晃动基座下的双位置参数辨识精对准仿真研究[J].计算机仿真,2009,26(1):83-87.BAI Liang,QUN Yong-yuan,SUN Li.A study of Double-position parameter identification alignment on oscillating base[J].Computer Simulation,2009,26(1):83-87.
[5]Ma Tao,Gao Yanbin.Application and comparison of two methods for alignment of FOG SINS[C]//2010 8th World Congress on Intelligent Control and Automation.Jinan,China,2010:3581-3584.
[6]Xu Bo,Sun Feng,Gao Wei.A FOG online calibration researeh based on high-preeision three axis turntable(El:20092312107165)[C]// International Asia Conference on Informatics in Control,Automation,and Roboties.CAR,2009:454-458.
[7]Xu Bo,Sun Feng,Gao Wei.An in dependent damped algorithm based on SINS for ship[C]//2009 International Conference on computer engineering and technology.ICCET.2009:88-92.
[8]Zhang H L,Wu W Q,et al.Improved multiposition calibration for inertial measurement units[J].Measurement Science and Technology,2010,20(1):1-11.
Rapid anti-interference method of two-position alignment of strapdown inertial navigation system
LIU Yong-hong1,LIU Ming-yong1,XIE Bo2
(1.Department of Navigation,Northwestern Polytechnical University,Xi’an 710072,China;2.The 16th Institute,China Aerospace Science and Technology Corporation,Xi’an 710100,China)
The classic two-position parameter identification alignment method of SINS uses horizontal velocity errors as measurements,and needs long time to identify some parameters.Besides,its convergent speed is affected by the initial value of recursive calculation.In this paper,an improved two-position alignment method is put forward which directly uses the horizontal specific forces in unit time as measurements.This method neglects the high-level items which are formed by errors.It changes cubic equation to linear model to estimate,which improves the speed of convergence.The tests by the two-position alignment method indicate that the new alignment method has many advantages such as simple arithmetic,small computational amount,quick alignment speed,strong anti-interference ability,high alignment precision,and it is not affected by the initial value of recursive calculation.
SINS;parameters identification;alignment;anti-interference;
U666.1
A
1005-6734(2014)03-0296-05
10.13695/j.cnki.12-1222/o3.2014.03.004
2014-01-24;
2014-05-12
船舶预研基金(No.12J4.2.4)
刘永红(1981—),女,博士研究生,从事惯性导航研究。E-mail:whitebirdfly@hotmail.com
联 系 人:刘明雍(1971—),男,教授,博士生导师。E-mail:liumingyong@nwpu.edu.cn

