均衡满意度的并行单色连通分支频谱分配算法

郑艳，徐国军，覃锡忠，贾振红

1.新疆大学信息科学与工程学院，乌鲁木齐 830046

2.中国移动通信集团新疆有限公司，乌鲁木齐 830046

均衡满意度的并行单色连通分支频谱分配算法

郑艳1，徐国军2，覃锡忠1，贾振红1

1.新疆大学信息科学与工程学院，乌鲁木齐 830046

2.中国移动通信集团新疆有限公司，乌鲁木齐 830046

1 引言

认知无线电（Cognitive Radio，CR）是当前一种常用的智能共享频谱资源的技术，它使频谱资源的使用更加科学合理化，从而改善了次用户频谱资源紧缺的问题[1-2]。CR技术是基于时间和空间都快速发生变化的动态环境中的，相比于传统信道指配里固定信道的分配，CR的频谱分配方法的有效性直接影响到该系统性能是否达到最优[3-5]。图论着色的频谱分配方案是如今主要的频谱分配方法之一，它将CR网络中的频谱分配问题映射成对无向图G的顶点着色问题[6-8]，是一种简单易行的方法。

图论的经典算法是颜色敏感着色[8]（Color Sensitive Graph Coloring，CSGC）算法，它考虑了频谱效益的差异性和干扰的频谱差异性，提出了带权重的复合图的列表着色[9]（List Coloring，LC）算法。然而CSGC算法存在的一个缺点就是运算量大，随着用户数和频谱数的增加运算量成非线性增加，导致了分配时间较长，大大降低了算法的有效性。判断一种算法的优劣要考虑它的有效性、公平性、扩展性和它是否使结果最优。为了改进CSGC算法，研究者大多从以下四个方面入手：一是考虑用户数对算法执行时间的影响，譬如分布式局部议价[10]（Local Bargaining，LB）算法，该算法每次分配时，利用前一次分配的信息，只对局部变动的拓扑进行议价分配，但是分配结果是次优的。二是考虑分配开销与频谱数目的关系，如并行频谱分配[11]（Parallel Algorithm of Spectrum Allocation，PASA）算法，该算法将干扰图分解成相比于CSGC算法的网络拓扑图简单的单色子图，对各子图的并行着色降低了算法的分配时间，但是每个单色子图只选择一个标号最大的顶点着色，由干扰关系更新拓扑后才能对该颜色下的其他顶点着色，并没有完全解决开销较大的问题。三是从图的结构出发，如今年发表的连通分支（Connected Branch of Spectrum Allocation，CBSA）算法，将图G分解为各个无干扰的连通分支，并且在并行处理各连通分支的频谱分配时，可以同时使多个无干扰的用户获取频谱，既保证了原算法系统收益不变化，又大大提高了整个系统的频谱分配速率[12]，但是各子图可能含有若干种颜色，一种颜色分配完后需要更新拓扑继续分配，依然没有完全解决开销较大的问题。四是从分配思想上出发，如改进的频谱分配[13]（Improved Algorithm of Spectrum Allocation，IASA）算法，打破先标号再分配的思想，同时进行标号和分配减少时间开销，但IASA算法在频谱分配过程中需要删除部分频谱减少运算来换取系统效用，导致频谱资源的复用率降低，得到的是比预期低的系统性能。此外，一些算法对用户的实际需求考虑得也不全面，大多只考虑了最大化系统带宽，不合理的分配造成了频谱资源的二次浪费[8-15]。为此，本文为了提高CSGC算法在动态分配中有效性和可扩展性，针对可并行计算的并行算法和连通分支算法存在的不足，提出了兼顾时间开销和用户需求的均衡用户满意度的并行单色连通分支频谱分配新算法，从根本上解决时间开销较大和用户满意度不均衡的问题。

2 用户满意度均衡的并行单色连通分支频谱分配算法原理

在PASA算法里基于频带正交假设，对某个频谱的使用不会对其他频谱造成干扰[8]，即对某个单色子图的着色不会影响到其他子图的着色。又由连通分量理论可知各连通分量子图之间不存在直接或者间接的干扰关系[12]，所以PASA算法和CBSA算法都能并行处理频谱分配问题。本文结合二者在频谱和系统拓扑结构上的特点将图G分解成各个无干扰的单色连通分量子图，同时对这些子图并行着色。得到了与PASA算法和CBSA算法相同的分配结果。由于系统拓扑图G分解成的单色连通分量子图数目可能会增多，而且每个子图只需要进行一次分配无需计算更新拓扑，所以该方法可以有效地减少时间开销。并且图分解是在分配频谱之前进行的，所以它可以应用在所有图论模型里。

然而上述分配并没有考虑到各个用户的实际需求，本文将继续改善分配结果，把满足需求和没有满足需求的用户分配到的频谱作调整，均衡了各用户的满意度，使未满足需求的用户满足需求或趋近于需求。

2.1 图论模型的数学描述

假设在一个分配周期里的认知网络固定。网络中有N个认知用户，存入集合V={n|n∈[1，N]}；M个频谱，存入集合Ms={m|m∈[1，M]}。将认知用户的频谱分配问题抽象成图G=(V，E，L)对顶点的着色问题[8]，则算法的数学模型可以由可用频谱矩阵L、效益矩阵B、需求矩阵D、干扰矩阵集合C、各用户有效分配频谱集合An、用户满意度大于1的用户集合F和小于1的用户集合K、可调整频谱集合U等来描述。

2.2 标号准则

假设效益矩阵B在分配周期内是不发生改变的。在着色时，将某颜色带来的收益越大的顶点，标上越大的号。对于各个单色连通分支顶点，本文制定了协作和非协作方式下的标号准则。

（1）协作式准则

其中Vmw是单色连通分支Gmw所含顶点的集合，bn，m是效益矩阵的元素，Dn，m代表在频谱m上与认知用户n有干扰冲突的用户数，即单色连通分支Gmw除去顶点n剩下顶点的个数。

（2）非协作式准则

在标号过程中，若出现最大标号顶点不唯一的情况，就随机选择其中的一个分配相应的颜色m。

2.3 用户满意度

用户满意度是指某用户的需求在频谱分配后得到满足的程度[14]，所以用户的满意度与用户的需求紧密相关，是衡量用户得到需求的重要参数。根据实际情况可以是基于业务的传输速率、用户等待时间、用户带宽、吞吐量等需求的满意度。本文针对可以累积叠加的用户需求制定的满意度如下：

其中An是顶点n分配到的颜色集合，dn是需求矩阵的元素，且当dn=0时，用户满意度sn=1。从式子中可以看出，sn≥1指用户需求得到满足，反之是指用户需求未得到满足。

2.4 可调整颜色的计算

假设对满足需求的顶点n*和未满足需求的顶点n作分配调整。本文算法定义的顶点n的可调整颜色集合计算式如下：

其中n的可用颜色集合Ln由可用频谱矩阵L得到，An*指顶点n*分配到的颜色集合，CMsAn指该网络的所有频谱集合Ms中未分配给顶点n的颜色集合。

考虑到取消某颜色的分配后满足需求的顶点可能会变成不满足需求的顶点，所以顶点n*和所有未满足需求的顶点都可以调整的颜色矩阵如下：

其中，r和n3分别指取消分配后顶点n*的需求依然满足的颜色集合R的元素和元素个数，n和n1分别指未满足需求顶点集合K的元素和元素个数。若r∈Un，则pr，n=1。所以pr，n=1指r是顶点n和n*都可以调整的颜色。

3 算法步骤

本文分为两个阶段进行频谱分配：一是根据信道效益情况对用户标号来完成初次频谱分配；二是考虑用户需求，调整某些频谱的分配得到最终的分配结果。在文献[11-12]中具体给出了对拓扑图的分块方法，文中不再过多讲解。而用户满意度均衡的调整分配算法在下面的流程图介绍中将详细给出。

根据本文的算法思想，具体的流程如图1所示。

该算法对系统拓扑图进行处理后，最终分解成了W个单色连通分量子图。为了表现出矩阵和集合的意义方便大家理解，由频谱特点分解成的子图命名为G1…GM，下标表示该子图是此颜色下的所有顶点的干扰关系。再由连通分量分解法分解成的单色连通分支Gmw(1≤W≤w)下标的首位和第二位指该连通分支顶点是关于m色的干扰关系并且是第w个连通分支。同理，顶点集合的名称也随着算法在改变，完成预分配后顶点存入的集合为Vmwn，是指将颜色m分配给了顶点n的单色连通分支Gmw的顶点集合。

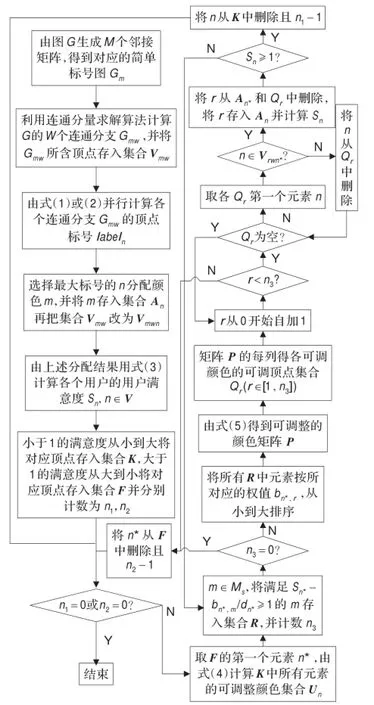
图1 算法流程图

完成第一阶段的预分配后要对各顶点的分配作调整。先将满意度最大的满足需求的顶点n*与所有未满足需求的顶点根据式（4）计算各自的可调整颜色集合Un。再计算取消分配仍能使n*满足需求的颜色集合R，为了不使满足需求顶点取消分配的颜色对它的需求影响太大，本文将集合内的元素按对n*的效益权值从小到大排序。由式（5）得到n*和K中元素都可以调整的各颜色下的未满足需求顶点集合Q，由于上面的排序，依次存入集合的是对顶点n*的需求影响小的颜色r下的满意度最低的顶点n。由上面的命名方式能快而直接地找到分配颜色r给n*的单色连通分支的顶点集合Vrwn*，并判断n是否也是该连通分支的顶点，如果是，就能取消给n*分配r而将r分给n。每次调整分配成功，n和n*的满意度都会变化。如果顶点n满足了需求，就从K中删除n，否则重新计算满足sn*-bn*，m/dn*≥1的颜色集合R，继续n*和n的颜色调整。如果最大满意度顶点n*取消了所有能调整分配的颜色后仍不能使未满足需求顶点满足需求，就从F中删除n*，直到F集合或者K集合中没有可调整分配的满足需求顶点或未满足需求顶点为止。

4 仿真结果与分析

下面对PASA算法和CBSA算法以及本文的PCU算法进行MATLAB仿真。仿真参数如表1所示，本文的用户效益权值和需求参考IEEE 802.22的设定，同时为了保证算法的准确性，仿真结果取多次随机的拓扑图G仿真结果的均值。

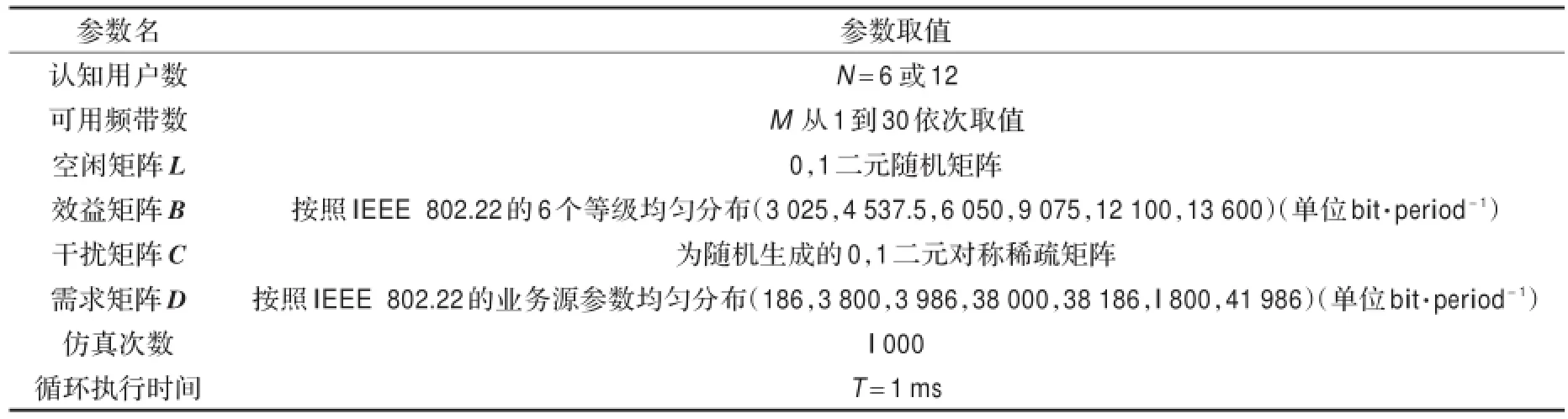
表1 仿真参数

4.1 时间开销

不考虑用户满意度的均衡，通过原理可以得到这三种算法频谱分配的时间取决于分解成的各小块所需要的分配时间的最大值，所以在相同系统拓扑图下，由于PCU算法进行着色的子图比PASA算法、CBSA算法的还要简单，所以新算法的运算量少，相应的时间开销更少。本文的比较采取文献[12]的方法，假设每次分配的循环执行时间为T，时间开销：t=h×T，其中h是总的执行分配次数。如图2和图3是用户数N取6时PASA算法、CBSA算法及PCU算法在协作准则和非协作准则下分别占CSGC算法的时间开销比例随频谱数目增加而变化的曲线。从图中可以看出，随着频谱数目M的增加，时间开销比例呈下降趋势。这是因为CSGC算法的分配循环执行次数随频谱数目的增加近似呈线性增加；PASA算法循环执行次数与待分配的频谱数目无关，循环执行次数几乎不变；CBSA算法循环执行次数略小于PASA算法[11-12]；而PCU算法执行一次便能完成分配无需循环。所以这三种算法的曲线近似于反比例函数图，但鉴于实际拓扑图的不同会出现一些突变点。

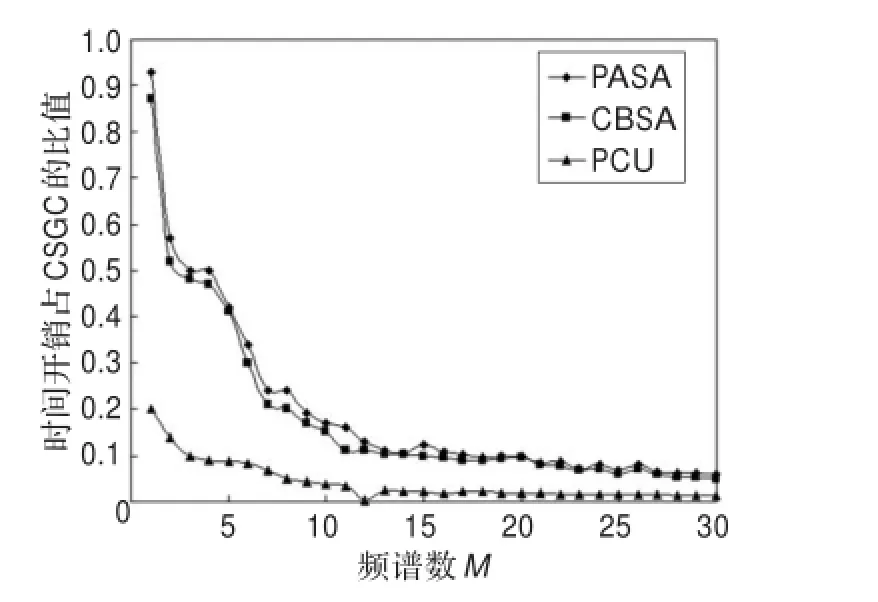
图2 协作式下频谱分配时间开销

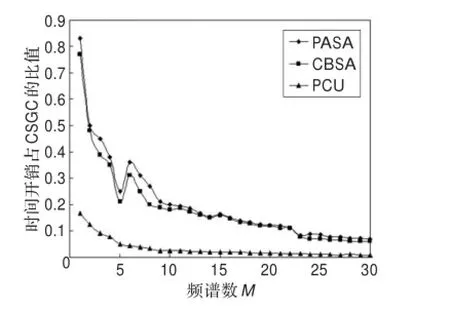
图3 非协作式下的频谱分配时间开销

4.2 满意用户比例

根据式（3）很容易便能计算出用户满意度大于等于1的满足需求用户数占总用户数的比例。如图4是用户数N取12时这三种算法的满意用户占总用户数的比例。随着频谱数目的增加，三种算法的满足需求用户比例都有提高。这是由于在分配周期内用户需求不变化的情况下，随着频谱数目的增加，频谱复用的程度有所增加，用户获得的信道效益增多，满足需求的用户也随之增加。还可以看出PASA算法和CBSA算法的满意用户所占比例完全相同，PCU算法满意用户比例最高并且随着频谱数目的增加所有用户最先达到全部满足需求的情况。这与PASA算法和CBSA算法的频谱分配相同，PCU算法根据用户需求调整分配使更多用户满足需求有关。再者，随机生成的拓扑图不同导致分配结果也有所不同，所以当频谱资源少的时候偶尔会出现满意用户，即满意用户的比例没有从0开始。

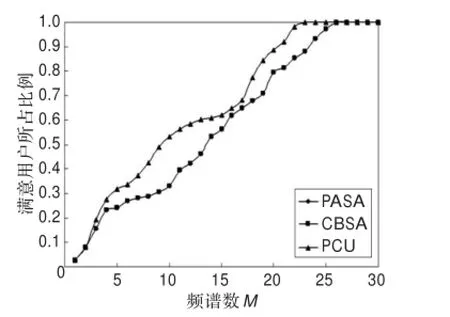
图4 满意用户所占比例

5 结论

本文研究了认知无线电网络中各类基于图论着色模型的频谱分配算法，在详细分析了CSGC算法的各种改进算法后，提出一种用户满意度均衡的并行单色连通分支频谱分配算法。该算法适用于所有基于图论的算法处理系统拓扑图，其特点是：将复杂的系统拓扑图分解成较多的可以并行计算的无干扰单色连通分量子图，无需循环更新拓扑图就能一次性完成分配，大大降低了时间开销。考虑到实际应用，又采取了均衡用户满意度的方法来调整频谱分配结果，使更多用户满足效益需求。并且与并行算法和连通分支算法在时间开销和满意用户比例方面进行比较，仿真表明：新的改进CSGC算法分配时间与频谱数无关，提高了可扩展性和有效地减少了时间开销，也更适于实际应用。

[1]Stotas S，Nallanathan A.On the throughput and spectrum sensing enhancement of opportunistic spectrum access cognitive radio networks[J].IEEE Transactions on Wireless Communications，2012，11（1）：97-107.

[2]Leshem A，Zehavi E，Yaffe Y.Multichannel opportunistic carrier sensing for stable channel access control in cognitive radio systems[J].IEEE Journal on Selected Areas in Communications，2012，30（1）：82-95.

[3]Janssen J，Kilakos K，Marcotte O.Fixed preference channel assignment for cellular telephone systems[J].IEEE Transactions on Vehicular Technology，1999，48（2）：533-541.

[4]Akyildiz I F，Lee Won-Yeol，Vuran M C，et al.A survey on spectrum management in cognitive radio networks[J]. IEEE Journal on Communications Magazine，2008，46（4）：40-48.

[5]MacKenzie A B，Reed J H，Athanas P，et al.Cognitive radio and networking research at Virginia tech[J].Proceedings of the IEEE，2009，97（4）：660-688.

[6]Nguyen M V，Lee Hwang Soo.Effective scheduling in infrastructure-based cognitive radio networks[J].IEEE Transactions on Mobile Computing，2011，10（6）：853-867.

[7]Rahwan I，Jahedpari F，Abdallah S.The dynamics of two cognitive heuristics for coordination on networks[C]//2010 IEEE Second International Conference on Social Computing，2010：473-479.

[8]Zheng Haitao，Peng Chunyi.Collaboration and fairness in opportunistic spectrum access[C]//IEEE 2005 International Conference on Communications，Washington DC，2005：3132-3136.

[9]Wang Wei，Liu Xin.List-coloring based channel allocation for open-spectrum wireless networks[C]//Proceedings of IEEE the 62nd Vehicular Technology Conference，Washington DC，2005：690-694.

[10]Cao Lili，Zheng Haitao.Distributed spectrum allocation via local bargaining[C]//Second Annual IEEE Communications Society Conference，2005：475-486.

[11]廖楚林，陈劼，唐友善，等.认知无线电中的并行频谱分配算法[J].电子信息学报，2007，29（7）：1608-1611.

[12]覃玉荣，胡虹梅.动态频谱分配的连通分支并行处理[J].电波科学学报，2012，27（1）：152-156.

[13]Wang Jiao，Huang Yuqing，Jiang Hong.Improved algorithm of spectrum allocation based on graph coloring model in cognitive radio[C]//2009 WRI International Conferences on Communications and Mobile Computing，Washington DC，2009：353-357.

[14]Gozupek D，Eraslan B，Alagoz F.Throughput satisfaction based scheduling for cognitive radio networks[J]. IEEE Trans on Vehicular Technology，2012，61（9）：1-16.

[15]Stotas S，Nallanathan A.Enhancing the capacity of spectrum sharing cognitive radio networks[J].IEEE Trans on Vehicular Technology，2011，60（8）：3768-3779.

ZHENG Yan1,XU Guojun2,QIN Xizhong1,JIA Zhenhong1

1.Institute of Information Science and Engineering,Xinjiang University,Urumqi 830046,China
2.Subsidiary Company of China Mobile in Xinjiang,Urumqi 830046,China

This paper analyzes the various spectrum allocation algorithms of graph coloring theory and concerns the problem of costing too much time.It combines connected component theory with the method that divides graph into subgraphs which have one color.A new method is proposed,which can parallel process all one-colored connected branches.This method can be applied to each algorithm to divide graph into small slices.And in view of the problem of unbalanced degree of users’satisfaction,an amendment is presented,which adjusts allocated spectrums to improve the proportion of satisfied users.The simulation results show that the proposed algorithm is fast and makes more users meet the needs of requirements effectively.

cognitive radio;spectrum allocation;graph coloring;parallel;connected branch

针对各类图论着色频谱分配算法的时间开销过大的问题，提出了一种并行单色连通分支处理拓扑图的方法。该方法结合连通分量理论和单色子图分解法，可应用于目前所有的图论着色模型的拓扑图分解中。并且根据认知用户的需求来调整分配使满意的用户比例增大，从而解决了分配结果存在的用户满意度不均衡情况。仿真结果表明，提出的算法是一种快速且能够使更多用户满足需求的有效方法。

认知无线电；频谱分配；图论着色；并行；连通分支

A

TN98

10.3778/j.issn.1002-8331.1210-0291

ZHENG Yan,XU Guojun,QIN Xizhong,et al.Parallel process one-colored connected branches in spectrum allocation algorithm based on degree of users’satisfaction balancing.Computer Engineering and Applications,2014,50（18）：197-201.

中国移动通信集团新疆有限公司研究发展基金项目（No.xjm2012-1）。

郑艳（1987—），女，硕士生，研究方向为无线网络优化和云计算；徐国军（1983—），男，网络工程师，研究方向为网络优化；覃锡忠（1963—），男，副教授，硕士研究生导师，研究方向为数字信号处理；贾振红（1964—），男，教授，博士生导师，研究方向为光信息处理、信号与信息处理、云计算等。E-mail：jzhh@xju.edu.cn

2012-10-29

2012-12-15

1002-8331（2014）18-0197-05

CNKI网络优先出版：2013-01-11，http://www.cnki.net/kcms/detail/11.2127.TP.20130111.0953.022.html