基于优势关系全序化的球队攻守能力评价研究
林伟华,李进金
漳州师范学院数学与信息科学系,福建漳州 363000
基于优势关系全序化的球队攻守能力评价研究
林伟华,李进金
漳州师范学院数学与信息科学系,福建漳州 363000
1 引言
足球比赛是一项胜负难料的体育运动,比赛中“以弱胜强”、“爆冷门”的现象时有发生,使得球王贝利被喻为“乌鸦嘴”,业内人士无奈地解释为“足球是圆的”。因而球队的竞技能力与比赛成绩呈现出一种不对等性。这种不对等性带给足球比赛扑朔迷离的悬念和猜想,注入足球运动强大的生命力和观赏魅力,造就了“足球世界第一运动”的誉称。以往,对一支球队攻守能力的强弱优差评价,通常凭借个人的主观感觉来判断。如何客观评价一支球队的攻守能力,这是当今足球界亟待解决的一个问题。
解决足球队攻守能力评价的难题,涉及的不确定因素较多,简单的数学工具显得无能为力。粗糙集理论[1]作为一种刻画不完备和不确定信息系统的数学工具,最早是由波兰科学家Z.Pawlak于1982年提出。它无需借助先验知识,能通过对数据的有效分析和推理,发现当中的隐含信息,揭示其潜在规律。经过国内外学者二十余年的研究,粗糙集已取得了一定的发展。目前,它已被广泛应用于机器学习、神经网络、模式识别、数据挖掘和设备故障等[2-6]领域。本文利用优势关系粗糙集方法,参照足球比赛技术统计的详实数据,对参赛球队的攻守能力进行量化分析,综合评价。分别从进攻能力、防守能力、攻守综合能力三个方面对参赛球队进行优势评价,从而得到球队攻守能力的合理排序关系。
2 预备知识
为了便于理解,首先介绍粗糙集理论的有关基本概念。
定义1.1[7]U上的关系R称为等价关系,若满足以下性质:
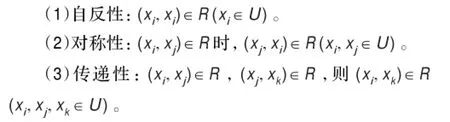

则[xi]≤B表示在属性集B条件下,优于对象xi的所有对象集合,称为xi的优势类。
经典粗糙集模型是建立在等价关系上的,而优势粗糙集模型是处理属性偏好有序的问题。偏序关系全序化的粗糙集方法是在偏序关系上建立优势关系,把连续值信息系统转化为优势关系模型,再通过关系模型得到对象间的排序。


3 基于粗糙集方法的球队进攻、防守、攻守能力的综合评价
3.1 评价指标确定和比赛数据的获取
通过查阅相关文献资料,从中收集反映比赛攻守能力的统计指标,初步建立本文研究的统计指标草案。在通过当面访谈和电子邮件方式对统计指标的合理性进行专家问卷调查,最终确立统计指标。具体情况如下:球队进攻能力的评价属性A确定为进球a1、射门a2、传威胁球a3、传球a4、角球a5、控球率a6;球队防守能力的评价属性B确定为失球b1、被射门b2、抢断b3;球队攻守能力的评价属性记为C。
本文主要选取了2012年欧洲杯官网16支参赛球队的比赛场均数据,将数据四舍五入保留小数点后两位得到如表1[8]所示。这16支球队分别为:西班牙x1,意大利x2,德国x3,葡萄牙x4,英格兰x5,捷克x6,希腊x7,法国x8,俄罗斯x9,克罗地亚x10,瑞典x11,丹麦x12,乌克兰x13,波兰x14,荷兰x15,爱尔兰x16。

表1 2012年欧洲足球锦标赛场均数据表次
3.2 评价步骤及计算结果
为了方便处理,在计算过程中,将表1中与防守能力呈负相关的统计指标“场均失球数”和“被射门场均数”设为负值。
步骤1由式(1)计算可得,
(1)各球队进攻能力的优势类分别为:
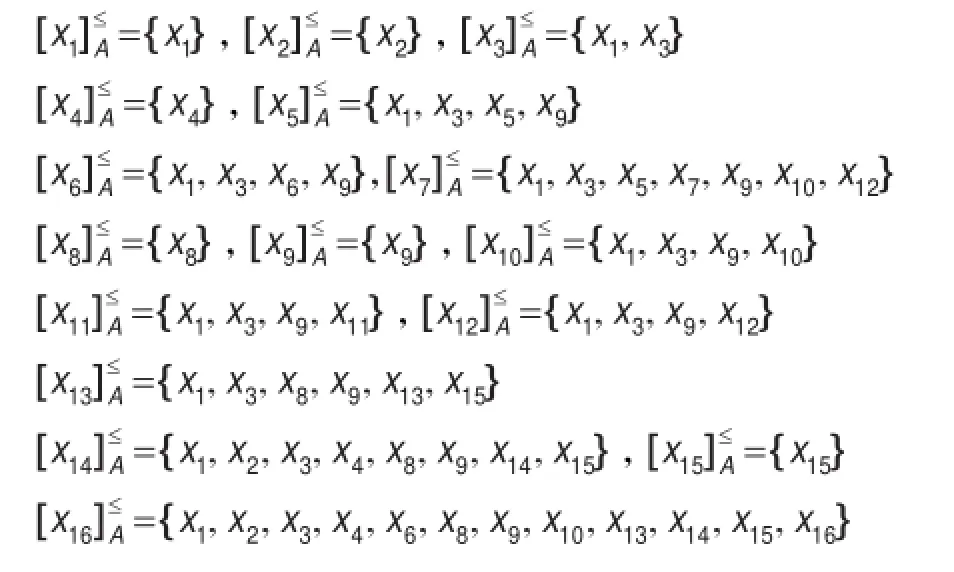
(2)各球队防守能力的优势类分别为:

步骤2由式(2)可得到球队之间的进攻和防守优势矩阵如表2和表3所示。
步骤3由式(3)可得球队的进攻综合优势度RA(xi)和防守综合优势度RB(xi)分别为:
(1)球队的进攻综合优势度RA(xi)为:
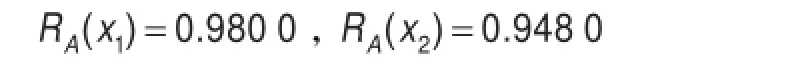
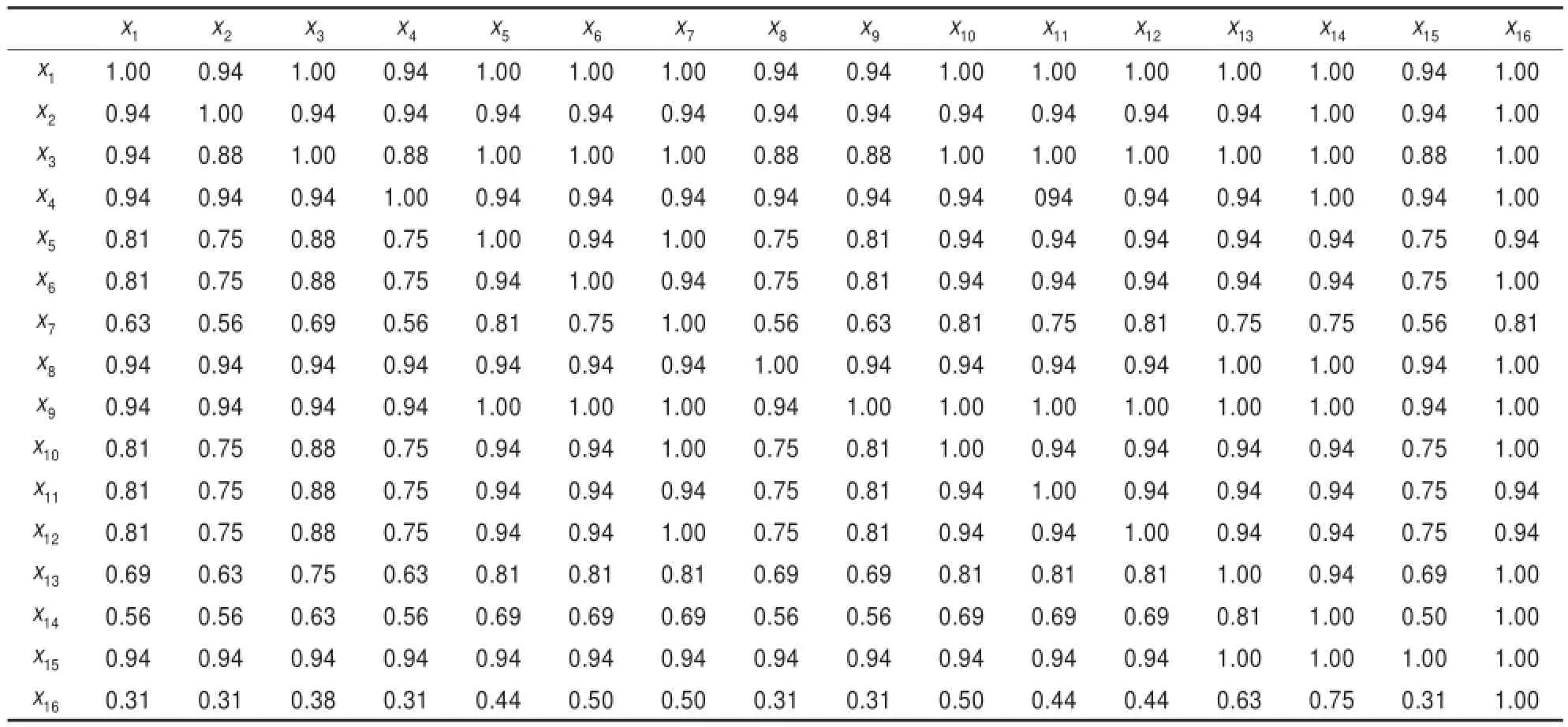
表2 球队之间的进攻优势矩阵
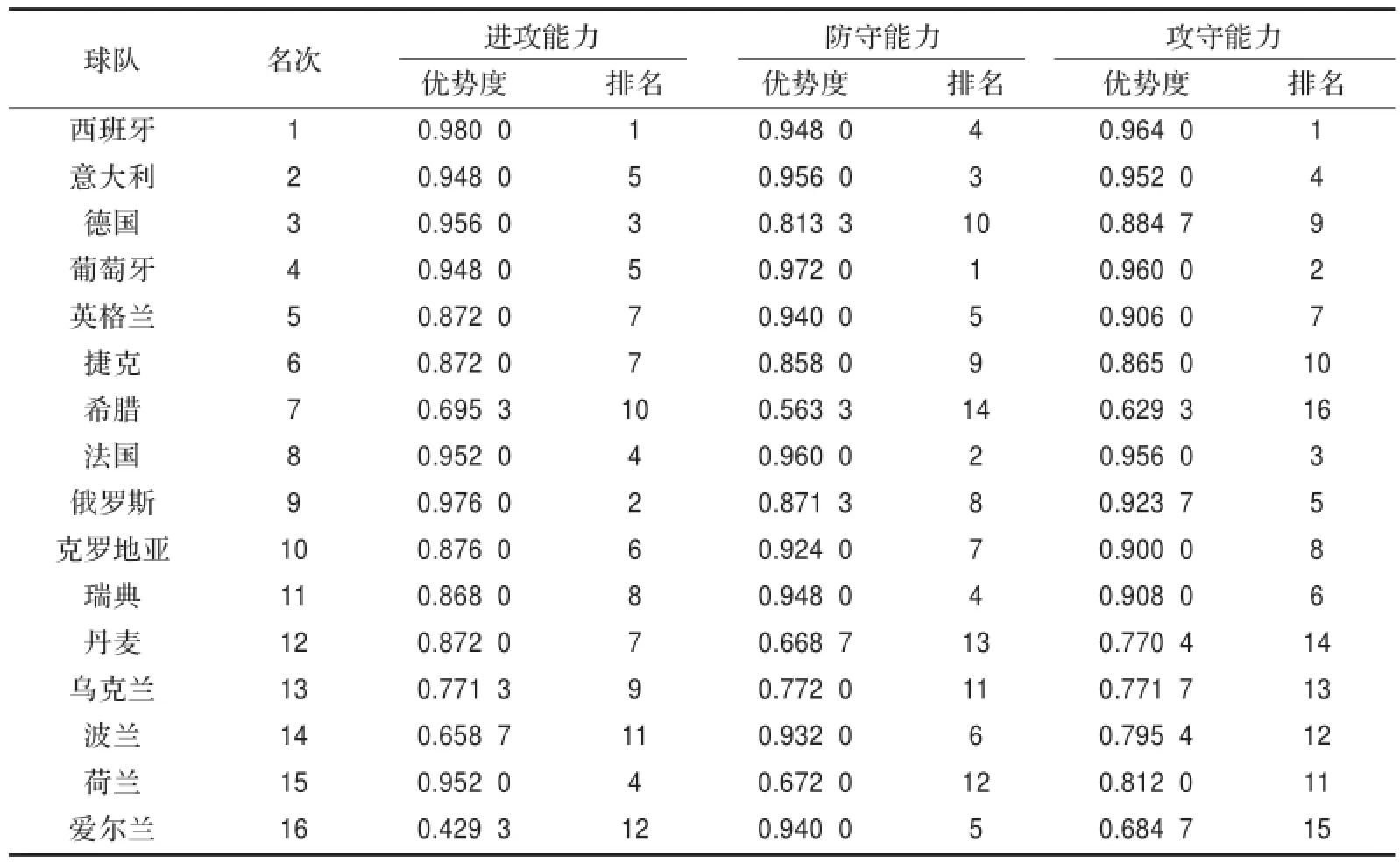
表4 2012年欧洲杯足球赛球队三个能力优势度对比一览表



查t值表,n′=16-2=14,t(14)0.05=2.145。算得t= 3.283 8>t(14)0.05=2.145,P<0.05。说明各球队比赛成绩名次与攻守能力排名之间具有显著性意义。优势度排名较客观真实地反映了比赛成绩,证明选用的进球、射门等九个指标能够有效地反映出球队攻守技战术能力。因此,优势关系粗糙集方法在足球比赛中具有实际应用意义。
优势度评价结果分析:
攻强守弱的典型代表球队(如俄罗斯和荷兰队)最终获取第九名和第十五名成绩;同时,守强攻弱的球队(如爱尔兰和瑞典队)最终成绩为第十六名和十一名;攻守平衡的球队(如西班牙、意大利和葡萄牙队)均获取了进入四强的佳绩。从优势度排序分析得知,足球比赛中球队不仅要具备强大的进攻能力,也应具备坚固的防守能力,只有达到攻守兼备和攻守平衡,才能取得好的成绩。
4 结论
本文通过基于优势关系的粗糙集方法,实现了对2012年欧洲足球锦标赛决赛的16支球队的进攻能力、防守能力和攻守综合能力的评价。而后又采用等级相关分析法检验显示,优势度评价结果较客观真实地反映了比赛成绩。优势关系粗糙集方法在足球比赛中具有实际运用意义,为足球比赛的技战术研究探索出了一种合理有效的数学研究方法。
[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Science,1982,11:341-356.
[2]杨常清.基于粗糙集的属性约简算法[J].西北大学学报:自然科学版,2012,42(2):223-225.
[3]杨冬风,杨冬秀.粗糙神经智能疑似乳癌图像分类方法研究[J].计算机工程与应用,2010,46(12):188-191.
[4]高建来,运士伟,张永胜.融合粗糙集与球形支持向量机的多分类识别[J].河南科技大学学报:自然科学版,2011,32(5):77-80.
[5]叶明全,伍长荣,胡学钢.基于粗糙集的医疗数据挖掘研究与应用[J].计算机工程与应用,2010,46(21):232-234.
[6]涂继亮,潘洪亮,董德存,等.融合粗糙集和证据理论的车地无线通信设备故障诊断[J].同济大学学报:自然科学版,2011,39(6):870-873.
[7]张文修,仇国芳.基于粗糙集的不确定决策[M].北京:清华大学出版社,2005:113-116.
[8]2012年欧洲足球锦标赛场均数据表[EB/OL].(2012-06-18)[2012-07-01].http://goal.euro2012.163.com/stat/teamrank/avg/ goals.html.
[9]戎家增,戎淼锋,林珑.现场体育统计方法[M].北京:人民体育出版社,1998.
LIN Weihua,LI Jinjin
Department of Mathematic and Information Science,Zhangzhou Normal University,Zhangzhou,Fujian 363000,China
By consulting documentations and questionnaires survey from exports,this paper sets up nine indexes of reflecting offensive and defensive ability about football teams,and collects these indexes’quantitative data from thirty-one matches between sixteen teams in the 2012 European Football Championships.Then it uses the theory of dominance relation rough set approach and grade correlation analysis to process and test it.The conclusion shows:it is more reliable to make quantitative evaluation of the indexes by adopting the theory of dominance relation rough set approach,which reflects objectively offensive and defensive ability of football teams.It reveals the tendency of football development,and explores a kind of suitable and available method for the ability of football teams in the meantime.
dominance relation;rough set approach;grade correlation analysis;offensive ability;defensive ability;offensive and defensive ability
通过查阅文献和专家问卷调查,选取了反映球队技战术能力的九项主要指标,对2012年欧洲杯足球赛决赛阶段的16支球队31场比赛进行统计,并运用优势关系粗糙集方法和等级相关分析法对所得数据进行处理和检验。结果表明:运用优势关系粗糙集方法对球队的技战术指标进行综合评价具有较高的可靠性,能够客观地反映各队技战术能力。在揭示足球技战术发展趋势的同时,探索出合理有效的量化评价球队技战术能力的方法。
优势关系;粗糙集方法;等级相关分析法;进攻能力;防守能力;攻守能力
A
TP18
10.3778/j.issn.1002-8331.1210-0062
LIN Weihua,LI Jinjin.Team offensive and defensive ability evaluation research based on dominance relation linearization method.Computer Engineering and Applications,2014,50(18):246-250.
国家自然科学基金(No.10971185,No.10971186,No.71140004);福建省资助省属高校科研专项(No.JK2011031)。
林伟华(1982—),女,在读硕士研究生,研究方向:粗糙集理论及其应用;李进金(1960—),男,教授,研究方向:拓扑学、粗糙集理论及其应用。E-mail:740816193@qq.com
2012-10-09
2012-12-17
1002-8331(2014)18-0246-05
CNKI网络优先出版:2013-01-11,http://www.cnki.net/kcms/detail/11.2127.TP.20130111.0951.006.html

