稀疏特征选择在过程工业故障诊断中的应用

于春梅

西南科技大学信息工程学院，四川绵阳 621010

稀疏特征选择在过程工业故障诊断中的应用

于春梅

西南科技大学信息工程学院，四川绵阳 621010

从一定意义上讲，故障诊断可以看成是用模式识别或者模式分类方法来解决故障的分类问题[1]。作为一种有效的降维手段，多元统计类方法在大规模工业系统，如过程工业的故障检测和诊断中发挥了重要作用。已经证明，如果直接对被测量采用主元分析法（Principal Component Analysis，PCA）或者Fisher判据分析法（Fisher Discriminant Analysis，FDA），得出的故障诊断结果并不理想。特征选择方法从原始空间选择子集，不仅可以降低数据维数，减少计算量；还可以去除冗余信息，有效提高故障诊断效果[2]。

影响特征选择的两个主要因素一是选择准则（影响精度），二是搜索算法（影响速度）。对于选择准则，一般采用可分性准则或基于时频分析的方法；搜索算法一般分为穷尽搜索、顺序搜索和随机搜索。对特征选择的改进要么在选择准则上有所创新，要么在搜索算法上下功夫，又或者二者兼而有之。随着对压缩传感研究的深入，不少学者意识到特征选择问题也可以表示成压缩传感的优化问题求解；这时，选择准则为优化目标函数，而搜索算法则是优化问题的求解算法。Yang等[3]将识别问题转化为寻找训练集中图像特征的稀疏表达问题；Cao等[4]利用稀疏优化问题选择基因SNP数据中的关键部分；二者均取得了较好的效果；但所采用的特征并不适用于过程工业数据。如何基于稀疏优化来选择过程工业数据的关键特征，使其利于对特定故障的诊断？基于稀疏表达的特征选择与传统的基于小波包和B距离的方法相比是否有优势？是本文的一个关键问题。

另外，近年来还有其他一些基于稀疏优化的算法在模式识别等领域取得了不错的效果。Zou等[5]基于PCA可以写成回归类型的优化问题，将1范数项加入优化准则，以得到PCA负荷向量的稀疏解，即为SPCA（sparsePCA）[6]；赵忠盖等[7]则引入了稀疏核主元分析（SKPCA），提高了监控的实时性。这两种方法虽然适用于过程工业数据，但只进行了故障监测的验证，没有相关故障诊断的结果。Qiao等[8-9]将稀疏保持投影（Sparsity Preserving Projection，SPP）应用于人脸识别，其思想是在低维空间保持稀疏重构关系。Wright等[10]采用稀疏表达分类器（Sparse Representation Classifier，SRC）进行人脸识别，取得了较好的效果，并被推广应用于其他应用[11-13]。以上方法虽然取得了不错的效果，但均缺乏过程工业故障诊断的有力例证。那么这些方法是否适用于过程工业的故障诊断？与特征选择后再进行故障诊断的方法相比，结果怎样？是本文的另一个关键。

本文接下来将首先介绍基于小波包和B距离的特征提取方法在故障诊断中的应用，接着从SRC、SPP和SPCA，引入本文所提出的基于稀疏表达的特征提取方法，并给出算法步骤。选择出关键变量后，再采用Bayes分类器诊断田纳西一伊斯曼（TE）过程的三类故障（http：// brahms.scs.uiuc.edu），最后给出本文方法与小波包分解和B距离方法，以及SRC、SPP、SPCA方法的比较结果。

1 基于小波包分解和B距离的特征选择

基于小波包分解和B距离的特征选择为特征选择的经典方法，本文将它们作为比较算法。下面简单介绍将它们用于TE过程特征选择的实施方法。

Bhattacharyya距离提供了一种两类数据的可分性测度，简称B距离，其定义为：

其中，(μ1，Σ1)，(μ2，Σ2)，分别为两类数据的均值和方差。特征选择即选择B距离大的变量而舍弃B距离小的变量。由于要测试的是三类故障，因此在排序时，对两两数据分别进行变量排序，以和作为每个变量的总排名依据。

与B距离不同，小波包分解考虑数据的时频域特性，由小波包分解系数的大小来确定哪些变量为重要变量。设xj(i)，i=1，2，…，l，j=1，2，…，52为TE过程的第j个检测变量的离散采样序列，选择二进小波包变换，在2N分辨率下分析，分解后的信号用xj(n，k)表示，这里n= 0，1，…，N表示分解的层数，k=1，2，…，2n代表频段。

定义原信号能量（第j个变量）：

由于各测量量具有不同的量程，为了避免大信号占绝对主导，定义分解后的能量和为：

设第j个测量量在正常模式下分解后的能量和为(j)，故障情况下分解后的能量和为(j)。计算各变量在不同模式下的能量差向量：

按照能量差的大小排序，并记下每个变量对应的序号。与B距离方法相同，在排序时，对两两数据分别进行变量排序，以和作为每个变量的总排名依据。

2 基于稀疏表达的特征提取

2.1 基于稀疏表达的模式识别方法

近年来，基于稀疏表达的方法在模式识别领域已经取得了不少成果，其中应用最为广泛的是稀疏表达分类SRC和稀疏投影保持SPP。这两者的核心均为求解典型的稀疏优化问题：

对于SPP，A为训练样本组成的矩阵，但每次抽出一列作为y，得到一个对应的s，设共有N个训练样本，则共进行N次优化求解，得到N个稀疏向量，这些稀疏向量在对应位置填充0以扩充向量，并组成稀疏权重矩阵；以此为基础，求降维矩阵，使稀疏重构误差最小，将降维的测试样本与降维的训练样本比较距离，即可实现归类。

除了这两种方法之外，还有一种PCA的稀疏版本，将PCA问题转化为回归问题，并增加1范数项。

其中，A为训练样本，Ai为A的第i行，n为样本数，βˆ为所求的稀疏负荷向量，k为主元数量。

以上三种方法中，SPP计算比较麻烦，且不能求解样本数大于变量数的情形；SRC已经被成功用于模式识别，但对于过程工业的故障诊断还没有例证；SPCA可以方便地实现检测，尚没有作者实现识别或诊断。将提出基于稀疏优化的特征提取方法，并与以上方法比较。

2.2 基于稀疏表达的特征提取

与以上方法不同，本文目的是从众多测量变量中选择出最利于分类的变量，然后采用Bayes分类器对测试样本进行分类。为了得到关键变量，对于A矩阵，不是直接由样本构成，而是分别用几类训练样本的均值和方差作为样本的特征来构成，其形式为：

表1 各种算法故障识别错误率（%）

其中，meani，vari，i=0，1，2分别代表故障i的均值和方差。对于输出y，参考用于分类判别的部分最小二乘（Partial Least Squares，PLS）的输出定义，3类共定义3列；第一列仅与故障0对应的元素为1，其余为0，第二列仅与故障1对应的元素为1，第三列仅与故障2对应的元素为1，形如：

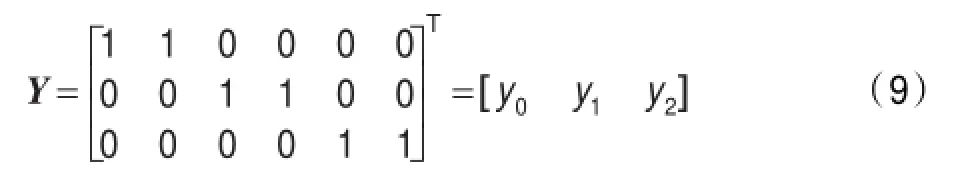
在满足Y=AS的条件下，为了得到稀疏解，求解l1范数约束的最小二乘拟合问题，并转化为无约束优化问题。

所求稀疏矩阵分别由与Y的各列对应的稀疏向量构成：

其中S表示不同变量对几类的贡献。如果所得的S是稀疏的，则表明少数不为0的元素对应的变量对分类起主导作用，将选择这些变量作为关键变量用于故障分类。

2.3 算法步骤

采用同伦算法来求解式（10）。同伦是指随着λ增大，目标函数从l2惩罚转为l1惩罚。式（10）λ≥0的解路径{λ:λ∈[0，∞)}是多边形的，而且，解路径的顶点对应解子集。子集为关于λ的分段常数，仅在λ的关键值（对应解路径的顶点）发生变化。这个演变的子集（evolving subset）叫做有效集（active set），基于此提出的同伦算法沿着解路径从一个顶点跳到另一个顶点，开始于空的有效集λ=0(λ→∞)，在每个顶点，通过添加或移出变量来迭代更新有效集。对于k稀疏问题，同伦算法在k步找到最优解[14]，其算法步骤如下：

3 仿真比较

采用田纳西-伊斯曼（TE）过程数据为仿真数据源，以故障0、1、2的训练数据和测试数据来进行仿真实验，故障0指正常工况，故障1和故障2均在第160个采样周期后引入；训练样本从第70个开始取，几种方法所选的关键变量均为6个，SPCA、SPP以及SRC的稀疏度为6。

根据前述的过程，采用小波包分解方法得到的关键变量为50，19，37，10，47，1；采用B距离方法得到的关键变量为18，19，1，50，47，44；采用本文方法得到的关键变量为44，47，19，16，3，2。提取完成后采用Bayes分类器进行分类，得到了不同训练样本的情形各种算法的识别错误率比较如表1。表中识别错误率是指故障1和故障2的漏报、误警和错分率之和的平均，由于故障1和故障2起始时均无故障，而是在第160个采样周期加入故障，因而这里的识别错误率也包含了对于故障0的识别，也即故障的检测。

由表1可以看出，多数情况下，SPCA比PCA效果要好，也比SRC和SPP好；无论是小波包、B距离还是本文方法，特征选择后的效果都要明显好于PCA和FDA，也普遍好于SPCA；在小样本情形，基于稀疏选择的诊断效果与其他两种选择方法相差不大，样本数大于50时，基于稀疏选择的效果明显好于其他两种。

4 结论

本文提出一种基于稀疏优化的方法来选择过程工业数据的关键特征，使其利于故障诊断。基于TE过程数据进行了仿真，一方面比较其与传统的PCA、FDA、基于小波包和B距离的特征选择方法；另一方面，将近年来常用的SRC、SPP和SPCA用于TE过程的故障诊断，与本文提出的特征选择方法后再用Bayes分类器进行故障诊断的方法相比较。从仿真结果可以得出以下结论：（1）几种稀疏算法中，SRC和SPP效果甚至不如普通PCA，SPCA则优势较为明显，可以说除SPCA外，其余两种并不适用于过程工业数据。（2）特征选择确实是提高故障诊断效果的有效手段，与传统的基于时频域和基于距离准则的变量选择方法相比，基于稀疏选择的诊断效果更好。（3）从算法的角度看，基于稀疏优化的方法还存在所需的训练样本少、计算简单的优点。综上所述，本文提出的稀疏方法可以胜任故障诊断前期的特征选择工作。

[1]于春梅.过程工业核化多元统计故障诊断方法研究[D].西安：西北工业大学，2010.

[2]吴斌，于春梅，李强.过程工业故障诊断[M].北京：科学出版社，2011.

[3]Yang A Y，John W，Ma Yi，et al.Feature selection in face recognition：a sparse representation perspective，Technical Report No.UCB/EECS-2007-99[R/OL].California：University of California at Berkeley 2007.http：//www.eecs.berkeley. edu/Pubs/TechRpts/2007/EECS-2007-99.html.

[4]Cao Hongbao，Wang Yuping.Integrated analysis of gene expression and copy number data using sparse representation based clustering model[C]//Proceedings of the ISCA 3rd International Conference on Bioinformatics and Computational Biology，BICoB-2011，New Orleans，Louisiana，USA，2011：172-177.

[5]Zou Hui，Trevor H，Robert T.Sparse Principal Component Analysis[J].Journal of Computational and Graphical Statistics，2006，15（2）：265-286.

[6]Lee S，Epstein M P，Duncan R，et al.Sparse Principal Component Analysis for identifying ancestry-informative markers in genome-wide association studies[J].Genet Epidemiol，2012，36（4）：293-302.

[7]赵忠盖，刘飞.基于稀疏核主元分析的在线非线性过程监控[J].化工学报，2008，59（7）：1773-1777.

[8]Qiao L，Chen S，Tan X.Sparsity preserving projections with applications to face recognition[J].Pattern Recognition，2010，43（1）：331-341.

[9]相文楠，赵建立.监督型稀疏保持投影[J].计算机工程与应用，2011，47（29）：186-188.

[10]Wright J，Yang A Y，Ganesh A，et al.Robust face recognition via sparse representation[J].IEEE Trans on Pattern Anal Mach Intell，2009，31（2）：210-227.

[11]董丽梦，李锵，关欣.基于稀疏表示分类器的和弦识别研究[J].计算机工程与应用，2012，48（29）：133-136.

[12]李心洁，王春恒.基于稀疏表达的视频文字检测[J].计算机工程，2011，37（6）：145-147.

[13]Gao Shenghua，Tsang Ivor Wai-Hung，Chia Liang-Tien. Kernel sparse representation for image classification and face recognition[C]//Proceedings of the 11th European Conference on Computer Vision：Part IV.Berlin Heidelberg：Springer-Verlag，2010：1-14.

[14]Donoho D L，Yaakov T.Fast solution of l1-norm minimization problems when the solution may be sparse[J]. IEEE Transactions on Information Theory，2008，54（11）：4789-4812.

YU Chunmei

School of Information Engineering,Southwest University of Science and Technology,Mianyang,Sichuan 621010,China

In this paper,a new sparse representation based feature selection method is proposed,in which the sample matrix is composed of the mean and variant of training sample,and testing sample is the index vector responding to sample matrix. Homotopy algorithm is used to solve the optimization problem.Traditional selecting methods based on wavelet package decomposition and Bhattacharyya distance methods,and recently used sparse methods,sparse representation classifier, sparsity preserving projection and sparse principal component analysis,are compared to the proposed method.Simulations show the proposed selecting method gives the improved performance on fault diagnosis with Tennessee Eastman Process data.

sparse representation;feature selection;fault diagnosis;process industry

提出一种基于稀疏表达的特征选择方法，用训练样本的均值和方差组成优化算法的样本矩阵，测试样本采用与样本矩阵对应的指示向量，采用同伦算法求解优化问题。给出了算法的详细流程，并与传统的B距离法和小波包变换特征选择方法以及近年来常用的稀疏表达分类、稀疏投影保持和稀疏主元分析针对田纳西-伊斯曼过程进行故障诊断结果比较，结果表明所提出的方法故障诊断的误报率较低。

稀疏表达；特征选择；故障诊断；过程工业

A

TP277

10.3778/j.issn.1002-8331.1210-0318

YU Chunmei.Sparse feature selection method for fault diagnosis of process industry.Computer Engineering and Applications,2014,50（18）：257-260.

国家自然科学基金（No.60802040）。

于春梅（1970—），女，博士，教授，主要研究方向为系统辨识，故障诊断，模式识别等。

2012-10-30

2012-12-20

1002-8331（2014）18-0257-04

CNKI网络优先出版：2013-01-15，http://www.cnki.net/kcms/detail/11.2127.TP.20130115.1140.008.html