基于稀疏主元分析的过程监控研究

彭必灿，张正道

江南大学轻工过程先进控制教育部重点实验室，江苏无锡 214122

基于稀疏主元分析的过程监控研究

彭必灿，张正道

江南大学轻工过程先进控制教育部重点实验室，江苏无锡 214122

1 引言

工业过程监控是一种确保产品质量的有效方法[1]。过去的20年里，多元统计方法在工业过程监控领域获得了广泛的应用，并取得了许多科研成果[2]。最常见的多元统计方法有主元分析（PCA）和最小二乘法（PLS）[3]等。

PCA是一种基于数据驱动的过程监控方法，并成功应用于各种化工过程[4-5]。由于不需要过程变量的精确数学模型，且能从大量杂乱无章的数据中提取出有效的信息，PCA方法简化了过程监控的操作程序，并提高了过程监控的效率[1-4]。PCA方法有两个理想化的假设：主元能够俘获数据的最大变化，以及最小的信息损失；主元间是独立的，因而一个主元与其他主元不相关[5]，这两个假设成为主元分析改进方法的切入点。通过引入T2和SPE的监控指标，PCA及其改进方法能进行故障检测，并具有较低的误检率和漏检率[6-15]。随着研究的深入，相关的过程监控方法获得了快速的发展，并成功解决过程监控领域的诸多问题。核主元分析方法的提出，解决了非线性过程的监控问题[16]；动态主元分析方法的提出，解决了过去时刻的变量对当前时刻过程监控的影响问题，增强了系统的动态特性[17]；高斯混合模型的提出[14]，解决了非高斯分布数据的过程监控问题。这些方法优化了过程监控的模型，并改进了监控性能，却也有局限性。比如在大的工业系统中，由于存在较多的过程变量，传统的过程监控方法往往计算量较大，进而影响计算效率和过程监控的实时性。稀疏化的思想成了解决大数据问题的有效方式，这种思想最早出现在Jilliffe的著作中[4]。Zou构建了稀疏约束函数，并成功将稀疏化思想引入到PCA中[18-19]。由于PCA进行投影时，在数据的方差最大化方向中，并非所有的变量都对方差具有同等的贡献，具体到主元的负荷向量中，即为：对方差贡献越小的变量，对应的负荷系数越小。稀疏化的PCA就是通过限制负荷向量中非零系数的个数而获得，即求解约束函数并获得稀疏的负荷向量，从而得到最优化的稀疏主元[6-7，20]。

本文研究了一种稀疏主元分析的过程监控新方法。该方法将稀疏性引入到PCA模型中，并建立了新的回归模型，利用lasso约束函数优化主元，从而求解得到稀疏化的主元，进一步提出了稀疏的监控指标。在仿真阶段，通过构建稀疏主元分析模型，研究了模型的稳定性，进而进行TE过程的实验，结果表明，该方法能够增强模型的稳定性，减小主元和监控指标的计算量，进一步提高参数的计算效率和过程监控实时性，最终能够实现及时有效的故障检测。

2 Lasso约束函数

构建向量Xj和Z的线性回归模型，进而引出lasso约束函数。假定样本的采样数为n，变量p为传感器数目，采样n次后得到样本矩阵X，任意选取Xj相关的主元列向量，定义为Z：

式中，λ为非负的参数，γj为对应的回归系数向量。lasso约束函数最初由Tibshirani在1996年提出，Efron进一步证实其为分段的线性函数[18]。式（3）中，在样本最小残差平方和之后，增加了一个新的约束式，即最小回归系数的绝对值之和。随着λ的增大，回归系数的绝对值之和将会越来越小，回归系数最终将收缩为0。

由式（3）可知，在lasso的估计作用下，估计结果中的非零系数最多只有min(p，n)个。当p＞＞n时，lasso的估计函数易收敛，原因在于lasso函数只是孤立的选择各个观测变量，却忽略了变量之间贡献的有序性。因此，Zou和Hastie提出lasso函数的改进模型[18-19]。假设有两个非负的参数λ1和λ2，约束函数en的估计算法如下：

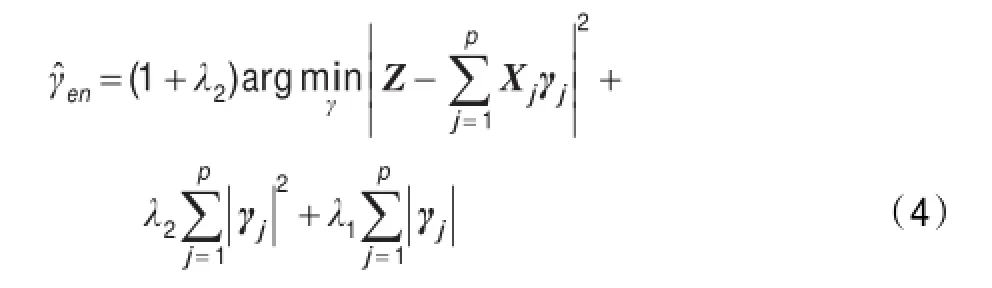
式中，若λ2的值为0，则式（4）回归为原始的lasso约束算法。相比式（3），由于增加了另外的参数λ2，lasso不再只是单独考察各个孤立的观测变量，更要考虑变量间相关性，并能选出最无关联的变量。若有p＞n，令参数λ2＞0，此时式（4）中的参数估计算法将覆盖所有变量，文献[18]证明了改进算法的优越性。

3 SPCA方法的过程监控

3.1 主元的稀疏性约束函数

将lasso约束函数引入到主元模型中，得到稀疏主元的约束性算法。假设此时的主元负荷向量为αk，样本数据集为X，其方差矩阵S为：

当t值减小时，较多的负荷向量系数将会收缩到0，因此t的大小影响主元的稀疏程度。定义一个简单的PCA模型，并对其进行回归分析，得定理1[18]。

定理1假设Y为样本数据的主元矩阵，Yj为Y的列向量，即为第j个主元，若存在参数λ＞0，则约束的估计函数为：

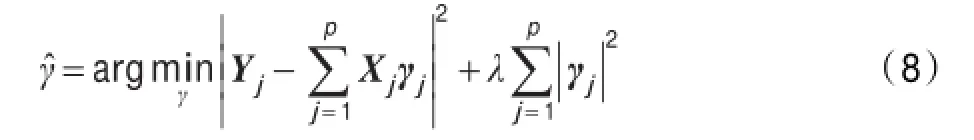
定理1可参照公式（3）推导，目的是将PCA模型转化为回归函数模型，定理中的参数λ为回归分析中的约束参数，并能用于主元的重构。引入另外的非负参数λ1，参考公式（4），定理1的扩展如下：

3.2 SPCA算法

由定理1可知，主元的稀疏化算法主要分两步，一是对PCA进行稀疏化的回归分析；二是利用约束参数μj估计稀疏后的主元。为了进一步研究稀疏主元分析算法，引入定理2[18]。

定理2令Xi表示矩阵X的第i个行向量，μi为μ的行向量，参数向量a和b的定义为：

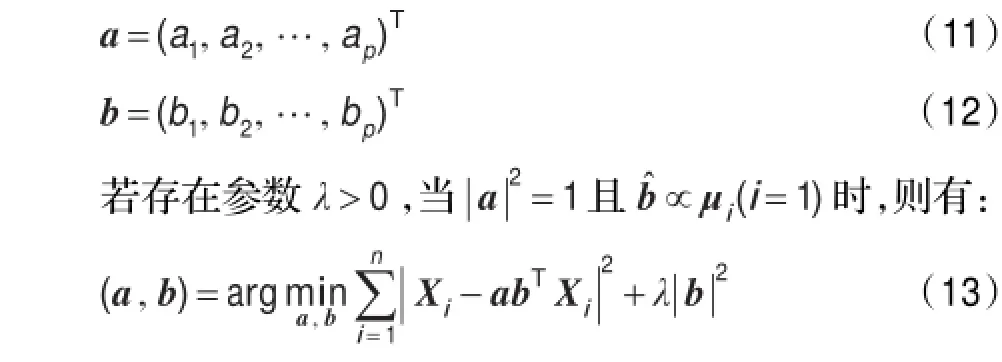
将定理2推广到k个主元的情况，得定理3[19]。

定理3选取样本的前k个主元，其中α和β为参数矩阵，且维数都为p×k，Xi仍为矩阵X的行向量，βj为β的列向量，若存在参数λ＞0，且αTα=Ik，推广定理2，得：

若令β=α，即回归为传统的PCA方法。将式（14）进一步改进，考虑k个主元的稀疏性，参考式子（4），当α仍然满足ααT=Ik时，得到函数式：

对稀疏主元分析的算法进行总结，得到k个主元的优化收敛算法步骤如下：

（1）求解样本矩阵的k个主元，参数矩阵α的初值为μi(i=1:k)。

（2）对于固定的α值，参考定理3和公式（17），在参数j=1，2，…，k时，计算稀疏约束的另一个参数β：

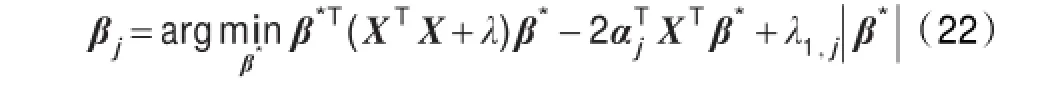
（3）求解出参数β后，参考定理4和公式（18），求解此时对应的参数α。对β值进行奇异值分解，有：

利用式子（21）计算α，并再一次更新α。

（4）重复（2）～（3），反复更新参数α和参数β，直到β收敛为止。

（5）参照式子（9），利用收敛后的最终β进行归一化，并求解最终的k个主元，得到稀疏最优解：

其中Sign为符号函数，而此时参数α对应为固定值。通过对SPCA算法的分析，得其流程图如图1。

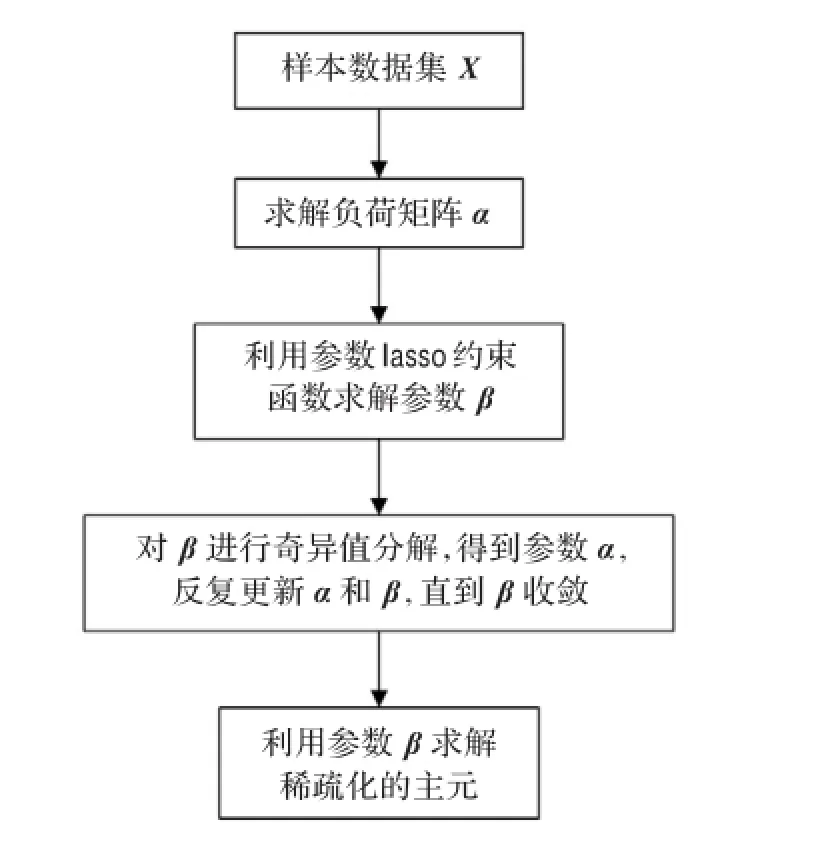
图1 SPCA算法流程图

3.3 SPCA方法的过程监控

在利用SPCA方法进行过程监控时，由于建立了稀疏模型，需要对传统的监控方法进行改进，并利用TE过程数据进行仿真研究。根据传统的SPE定义，改进后的SPE计算式如下：

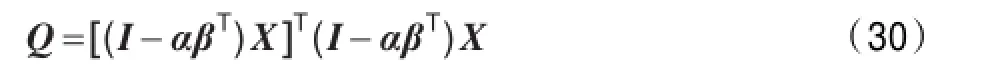
式中，α和β为稀疏参数，阈值Qα的计算式如下：

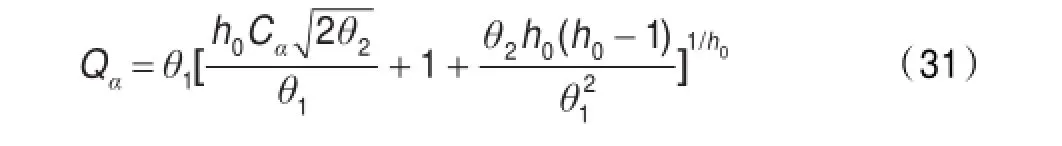
其中Cα是置信度为(1-α)的正态分布点，式中参数h0和θi的定义如下：

式中参数Fα(a，n-a)是一种F分布，且置信度为(1-α)，自由度为α，分位点为a和n-a。得到监控指标计算式后，选取TE过程数据[21]对SPCA算法进行仿真研究。SPCA模型的过程监控步骤如下：

（1）从TE过程数据集中获取采样数据，并按正常条件下模型的均值和方差进行标准化，得到训练和测试的样本数据。

（2）给定训练数据集，利用lasso约束函数对样本数据载荷矩阵进行稀疏化，并求解最优的稀疏参数α和β。

（3）给定测试数据集X，更新参数α和β，并利用式（24）计算稀疏化后的主元，详细过程参见SPCA的收敛算法。

（4）计算测试数据的SPE和T2统计量。

（5）监视SPE和T2是否超过正常条件下的建模值。

4 SPCA方法的仿真研究

4.1 SPCA模型的稳定性研究

选择文献[18]中的数据集对PCA和SPCA模型的稳定性进行对比研究，数据集中每个变量的维数为1 500，500个变量构成测试数据集。设定此时的噪声规则，即为：0到1之间的随机数。选取主元的个数为3，利用matlab进行实验仿真，设定0～1 s内采样500次，作为500个变量，3个主元分别为3种函数，图2中用不同颜色加以区分。利用仿真图进行对比研究，其中图2（a）为PCA方法的主元贡献图，图2（b）为SPCA方法的主元贡献图。

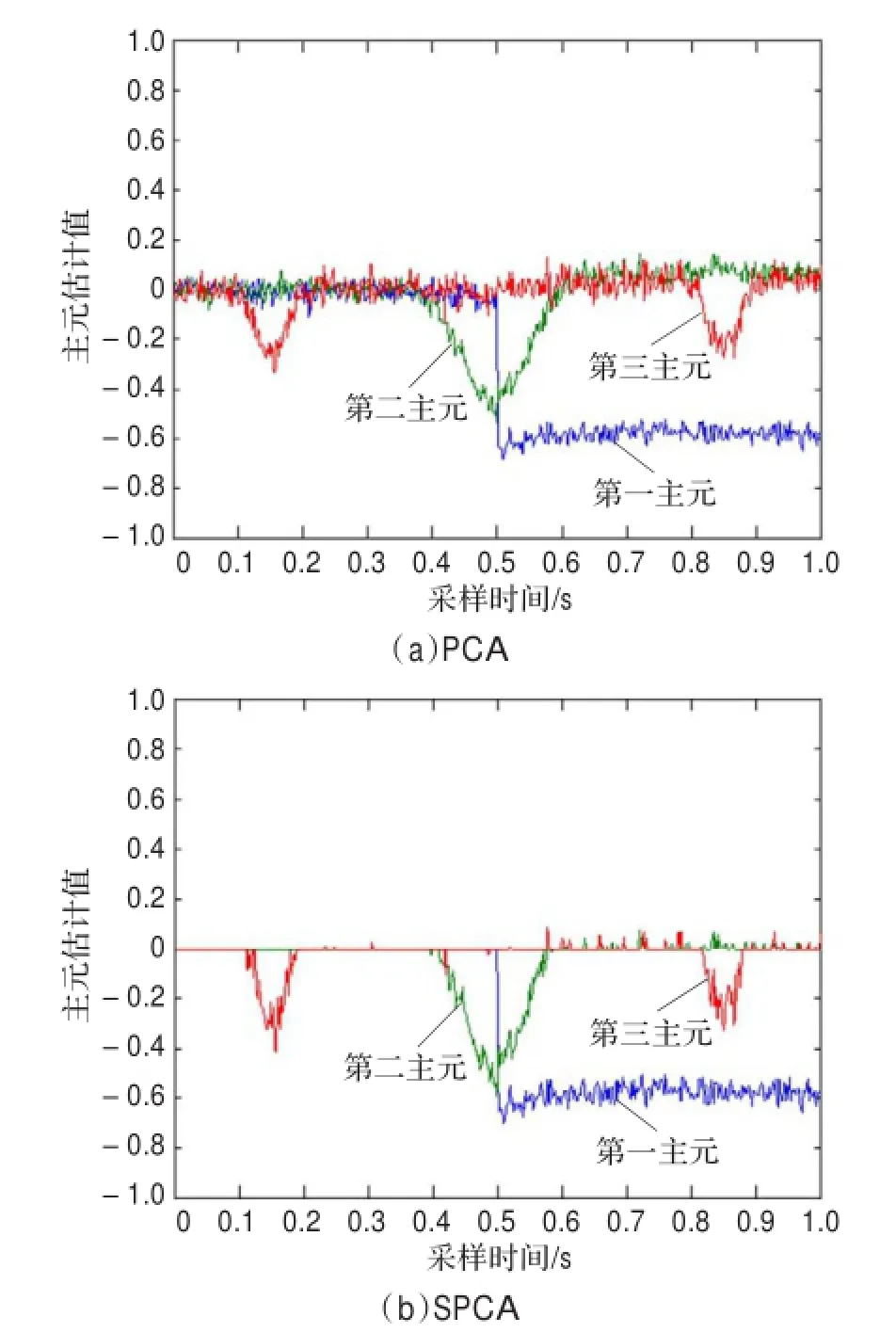
图2 PCA与SPCA的主元贡献分析

对比图2（a）、（b），由于离横坐标轴近的变量对函数的影响小，可视其对主元的贡献小，而离横坐标轴远的点对函数的影响大，可视其对主元的贡献大。通过图2（a）、（b）的对比研究，加入噪声后，传统PCA方法中贡献较小的变量波动明显，表明其对主元产生影响，如图2（a）中的横坐标轴附近的波动较大；改进后的SPCA方法中，只有贡献较大的变量对主元有较大影响，而贡献小的变量对主元几乎无影响，如图2（b）中的横轴附近几乎无波动。产生这种现象的原因为：SPCA模型稀疏化了载荷矩阵，并求解约束函数而得到优化后的主元，减少了无关变量对主元的影响。仿真结果表明，相对于传统的PCA模型，SPCA模型呈现出较好的稳定性，进一步需研究SPCA模型的过程监控效果，并利用TE过程数据进行仿真对比。

4.2 SPCA方法的TE过程监控

将SPCA方法的过程监控指标应用到TE过程，并利用仿真结果评价这种方法的性能。TE过程数据是一组工业过程仿真数据[15]，由美国Eastman化学公司的Downs和Vogel在1993年提出，大量的文献引用其作为数据源，来进行控制、优化、过程监控和故障诊断等研究。

TE过程实际上模仿了真实的化工过程，共有5个主要的操作单元，分别为：反应器、冷凝器、气液分离器、循环压缩机、汽提塔，其流程图如图3。

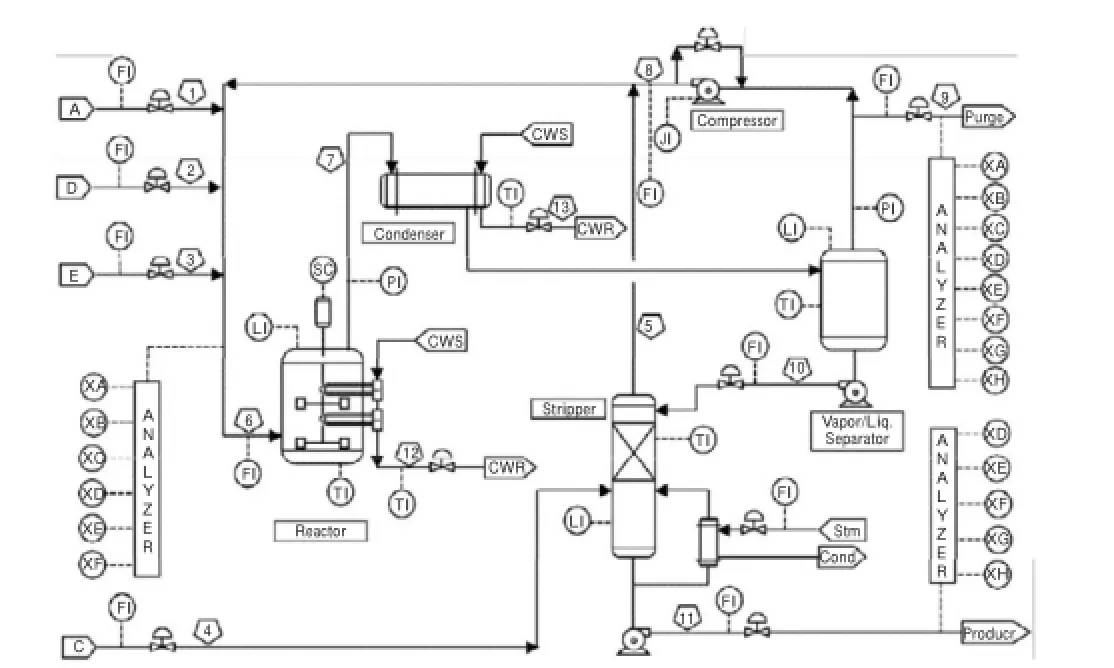
图3 TE过程流程图

选取TE过程数据对SPCA模型进行训练，数据集包括480组采样数据，每组采样数据有22个变量。再利用测试数据更新SPCA的模型参数，计算新的监控指标，并记录下实验结果。此时的方差贡献率设定为0.9，统计阈值的置信度α设定为0.97，得到PCA与SPCA方法的SPE和T2的统计监控图如图4。

图4（a）～（b）为PCA方法的故障检测效果图，样本数据共采样480次，采样的时间间隔为3 min，得到480个样本。其中图4（a）和（b）分别为PCA的T2和SPE统计图，曲线对应为监控指标值，并且虚线为控制限。当有监控值超出控制限时，判定该样本时刻系统发生故障。而图4（c）和（d）也分别对应SPCA方法的T2和SPE的监控指标。对比PCA和SPCA方法的监控效果，当分别利用PCA模型和SPCA模型监控时，T2统计图都在250到300个样本间超出控制限，判断该样本时刻内系统发生故障，需利用SPE监控指标进行进一步的对比研究。计算测试样本的SPE值，并进行对比图的详细分析，观测到PCA的监控图在270个样本时刻明显超出控制限，判断该样本时刻系统出现故障，而SPCA监控图在250个样本时刻明显超出控制限，判定故障出现在250个样本时刻。分析PCA方法和SPCA方法的监控效果，PCA方法在监控图上出现了一定程度的时间延迟，产生这种现象的原因为：SPCA方法稀疏化了建模数据，减少了模型参数和监控指标的计算量，缩短了计算时间，并提高了计算效率，进而提高了故障检测的实时性。进一步得出结论：PCA方法和SPCA方法的TE过程监控结果明显，都能够检测出系统故障，然而SPCA方法的实时性稍好。为了进一步验证SPCA方法的计算效率，分别测量PCA方法和SPCA方法的计算时间，并对结果进行对比研究。

选取一组测试数据进行故障检测，利用Matlab计算TE过程监控的程序运行时间，得到PCA模型和SPCA模型的监控计算时间，结果对比如表1。

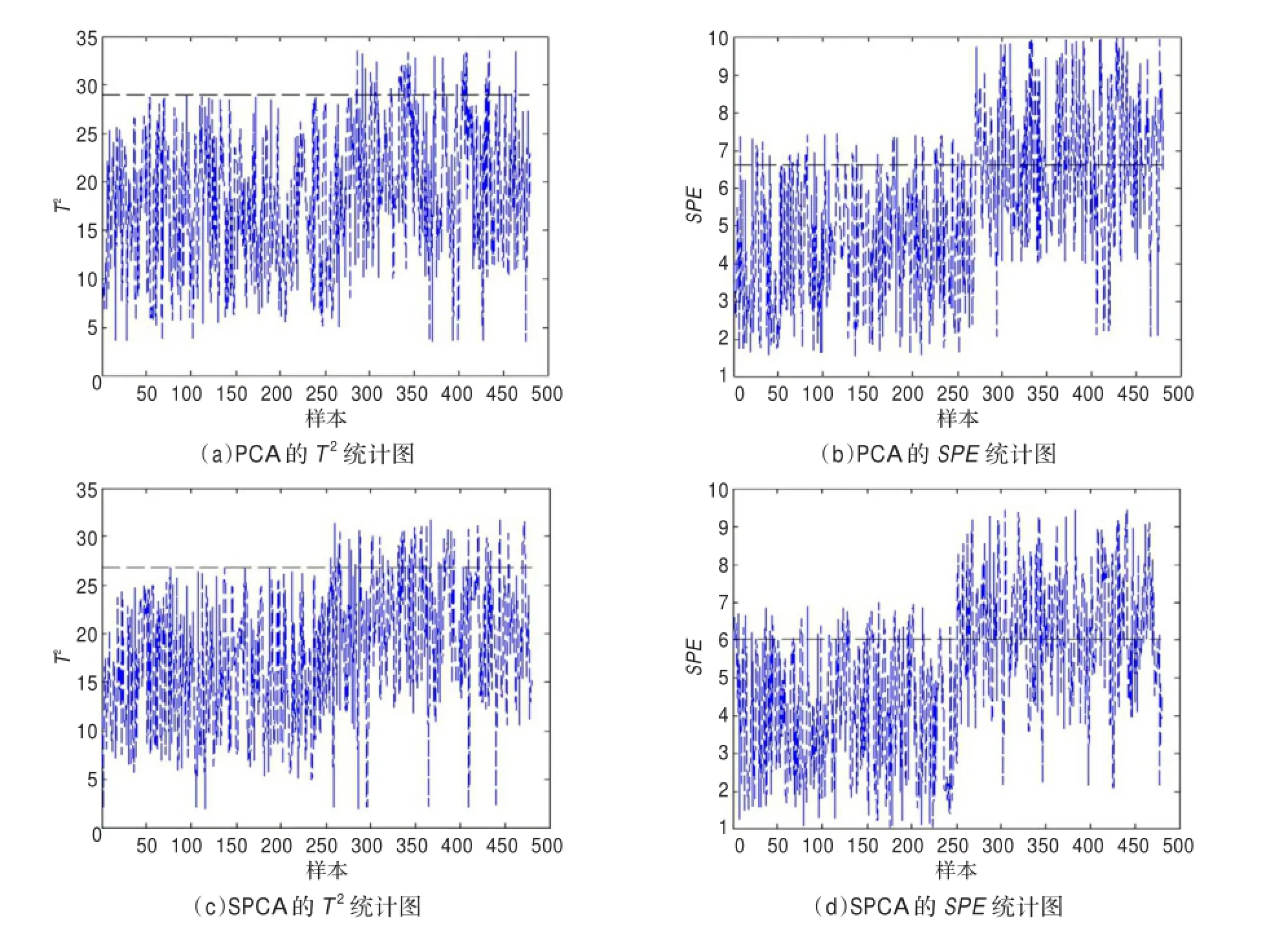
图4 PCA与SPCA方法的监控效果对比

表1 SPCA与PCA计算时间对比

对比表中的数据，SPCA方法对测试数据的监控计算时间为0.942 s，相比PCA的1.364 s较为减少，运算效率得到提高，表明SPCA方法对监控模型具有一定的优化作用，通过减小参与计算的数据量，进一步提高运算效率和过程监控的实时性。

5 结束语

本文提出了一种基于SPCA模型的过程监控新方法。首先对样本数据的主元进行稀疏化建模，减少了无关变量对方差的干扰，进而提高了模型的稳定性。由此构建稀疏的监控指标，建立稀疏模型的SPE和T2统计量，并对PCA方法和SPCA方法的过程监控效果进行对比研究。通过模型的仿真效果对比，表明了SPCA监控方法能减小模型和监控指标的计算量，缩短过程监控的计算时间，并提高监控的实时性，是一种有效的状态监控方法。

[1]Chiang L H，Russell E L，Braatz R D.Fault detection and diagnosis in industrial systems[M].New York：Springer-Verlag，2001：15-25.

[2]Bishop C M.Pattern recognition and machine learning[M]. New York：Springer-Verlag，2006：559-599.

[3]Ding S.Model-based fault diagnosis techniques[M].New York：Springer-Verlag，2008：13-49.

[4]Jolliffe I T.Principal component analysis[M].2nd ed.New York：Springer-Verlag，2002：167-195.

[5]Qin S J.Statistical process monitoring：basics and beyond[J]. Chemometrics，2003，17：480-502.

[6]向馗，李炳南.基于稀疏主元分析的微伏级T波交替幅度量化[J].生物医学工程学杂志，2012，29（5）：954-982.

[7]刘中杰，庄丽葵，曹云峰，等.基于主元分析和稀疏表示的SAR图像目标识别[J].系统工程与电子技术，2013，35（2）：282-286.

[8]徐毅，赵东娟，梁久祯.二维类增广PCA及其在人脸识别中的应用[J].计算机工程与应用，2012，48（1）：202-204.

[9]陈勇，梁军.基于PCA的多变量控制系统的故障监测与诊断[J].工程设计学报，2002，9（5）：257-260.

[10]赵忠盖，刘飞.基于稀疏核主元分析的在线非线性过程监控[J].化工学报，2008，59（7）：1773-1777.

[11]肖应旺，徐保国.改进PCA在发酵过程监测与故障诊断中的应用[J].控制与决策，2005，20（5）：571-574.

[12]王海清，宋执环，王慧.PCA过程监测方法的故障检测行为分析[J].化工学报，2002，53（3）：297-301.

[13]许仙珍，谢磊，王树青.基于GMM的多工况过程监测方法[J].计算机与应用化学，2010，27（1）：17-21.

[14]Benaicha A，Mourot G，Benothman K，et al.Determination of principal component analysis models for sensor fault detection and isolation[J].International Journal of Control，2013，11（2）：296-305.

[15]Chen Tao，Sun Yue.Probabilisticcontributionanalysis forstatisticalprocessmonitoring：amissingvariable approach[J].Control Engineering Practice，2009，17（4）：469-477.

[16]薄翠梅，李俊，陆爱晶，等.基于核函数和概率神经网络的TE过程监控研究[C]//第26届中国控制会议论文集.北京：北京航空航天大学出版社，2007，5：511-515.

[17]Treasure R J，Kruger U，Cooper J E.Dynamic multivariate statistical process control using subspace identification[J]. Journal of Process Control，2004，14：279-292.

[18]Zou Hui，Hastie T，Tibshirani R.Sparse principal component analysis[J].Journal of Computational and Graphical Statistics，2006，15（2）：265-286.

[19]Zou Hui，Hastie T.Regularization and variable selection via the elastic net[J].Journal of the Royal Statistical Society，2005，67（2）：301-320.

[20]向馗，李炳南.主元分析中的稀疏性[J].电子学报，2012，40（12）：2525-2532.

[21]Downs J J，Vogel E F.A plant-wide industrial process control problem[J].Computer and Chemical Engineering，1993，17（3）：245-255.

PENG Bican,ZHANG Zhengdao

Key Laboratory of Advanced Process Control for Light Industry,Ministry of Education,Jiangnan University,Wuxi,Jiangsu 214122,China

Principal Component Analysis（PCA）is a multivariate statistical technique,with a range of applications in data processing and dimensionality reduction.Over the past two decades,PCA method has also been widely applied to various kinds of industrial processes for process monitoring and fault diagnosis with some successes.Due to the increasing volumes of data,process monitoring methods which are based on PCA approaches suffer many limitations,such as great calculation loads and poor real-time performance.In this paper,a new method called Sparse Principal Component Analysis（SPCA）is developed in process monitoring,using the lasso（least absolute shrinkage and selection operator）to produce modified principal components with sparse loadings.And the SPCA can be formulated as a regression-type optimization function to achieve the main elements of choice.Furthermore,the fault detection is then performed by a detection index using model parameters,and the sparse principal component analysis is used in the Tennessee Eastman process（TE processes）monitoring for simulations.Compared with the traditional principal component analysis method,this SPCA approach builds a model based on the sparse modeling data.Therefore it can reduce the amount of calculations and improve the real time performance.As the SPCA model is applied to simulate with real data,the results show that it has better effectiveness in TE processes.

least absolute shrinkage and selection operator（lasso）;Sparse Principal Component Analysis（SPCA）;state monitoring;Tennessee Eastman（TE）processes

主元分析（principal component analysis）是一种多元统计技术，在过程监控和故障诊断中具有广泛的应用。针对过程监控中数据量大的特点，提出一种稀疏主元分析（sparse principal component analysis）方法，通过引入lasso约束函数，构建稀疏主元分析的框架，将PCA降维问题转化为回归最优化问题，从而求解得到稀疏化的主元，并提高了主元模型的抗干扰能力。由于稀疏后主元相关的数据量减少，利用数据建立过程监控模型，减少了计算量，并缩短了计算时间，进而提高了监控的实时性。利用田纳西伊斯特曼过程（TE processes）进行实验仿真，并与传统的主元分析方法进行对比研究。结果表明，新提出的稀疏主元分析方法在计算效率和监控实时性上均优于传统的主元分析方法。

最小绝对收缩和选择算子（lasso）；稀疏主元分析；状态监控；田纳西伊斯特曼（TE）过程

A

TP306+.3

10.3778/j.issn.1002-8331.1307-0368

PENG Bican,ZHANG Zhengdao.Process monitoring research based on sparse principal component analysis. Computer Engineering and Applications,2014,50（18）：240-245.

国家自然科学基金（No.61374047）；中央高校基础研究项目（No.JUSRP51322B，No.JUSRP111A49）。

彭必灿（1988—），男，硕士研究生，研究领域为控制工程、故障诊断；张正道（1976—），通讯作者，男，博士，副教授，研究领域为状态监控与故障诊断、故障预报。E-mail：wxzzd@hotmail.com

2013-07-29

2013-10-15

1002-8331（2014）18-0240-06

CNKI网络优先出版：2013-12-19,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1307-0368.html