基于ELM和FOA的股票价格预测

李栋，张文宇

西安邮电大学管理工程学院，西安 710061

基于ELM和FOA的股票价格预测

李栋，张文宇

西安邮电大学管理工程学院，西安 710061

1 引言

大量研究表明，股票价格是一个动态的、非线性的复杂系统，具有突发性、随机性和规律性等特点，传统线性模型已不适用于日趋复杂化的股票价格研究。神经网络是一种对非线性数据具有良好预测性能的工具，目前已经成为股票价格预测的研究热点之一[1-2]，但神经网络存在训练速度慢、参数寻优难、过拟合、局部最优以及隐含层节点数人为指定等问题，这些问题直接影响了股票价格的预测精度[3-4]。

为了克服神经网络存在的这些问题，Huang等提出了极限学习机（Extreme Learning Machine，ELM）[5-6]。ELM是依据摩尔-彭罗斯（MP）广义逆矩阵理论提出的一种机器学习新算法，该算法仅通过一步计算即可解析求出学习网络的输出权值。同神经网络和支持向量机相比，ELM极大提高了网络的泛化能力和学习速度。但是，由于ELM存在随机给定左侧权值和隐含层阈值的缺陷，使得回归模型容易产生泛化性能不高与稳定性不理想等问题[7-10]。

本文针对极限学习机稳定性不理想的问题，提出了一种基于改进果蝇优化算法的极限学习机股票价格预测方法。该方法首先采用因子分析法综合股票价格的各原始输入指标，消除指标数据之间的冗余，减少极限学习机的输入参数，这样做有助于提高极限学习机的学习效率；然后利用果蝇优化算法优化极限学习机的输入层与隐含层连接权值和隐含层阈值，确定极限学习机预测模型的各个参数；最后使用优化得到的极限学习机预测模型对股票价格进行预测，并将预测结果与实际值进行比较，验证模型的有效性。

2 极限学习机

极限学习机（Extreme Learning Machine，ELM）是一种针对单隐层前馈神经网络（Single-hidden Layer Feedforward Neural Networks，SLFN）的学习算法。与传统神经网络训练方法相比，该算法具有学习速度快，泛化性能好等优点[11-12]。SLFN的基本结构如图1所示。

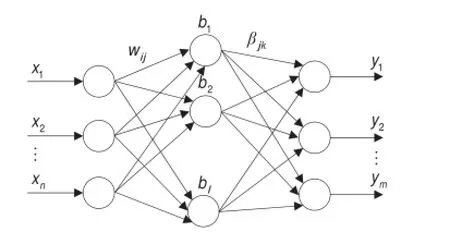
图1 单隐层前馈神经网络结构图

设隐含层的神经元个数为l个，并给定Q个股票价格训练样本(xi，yi)和一个任意区间无限可微的激活函

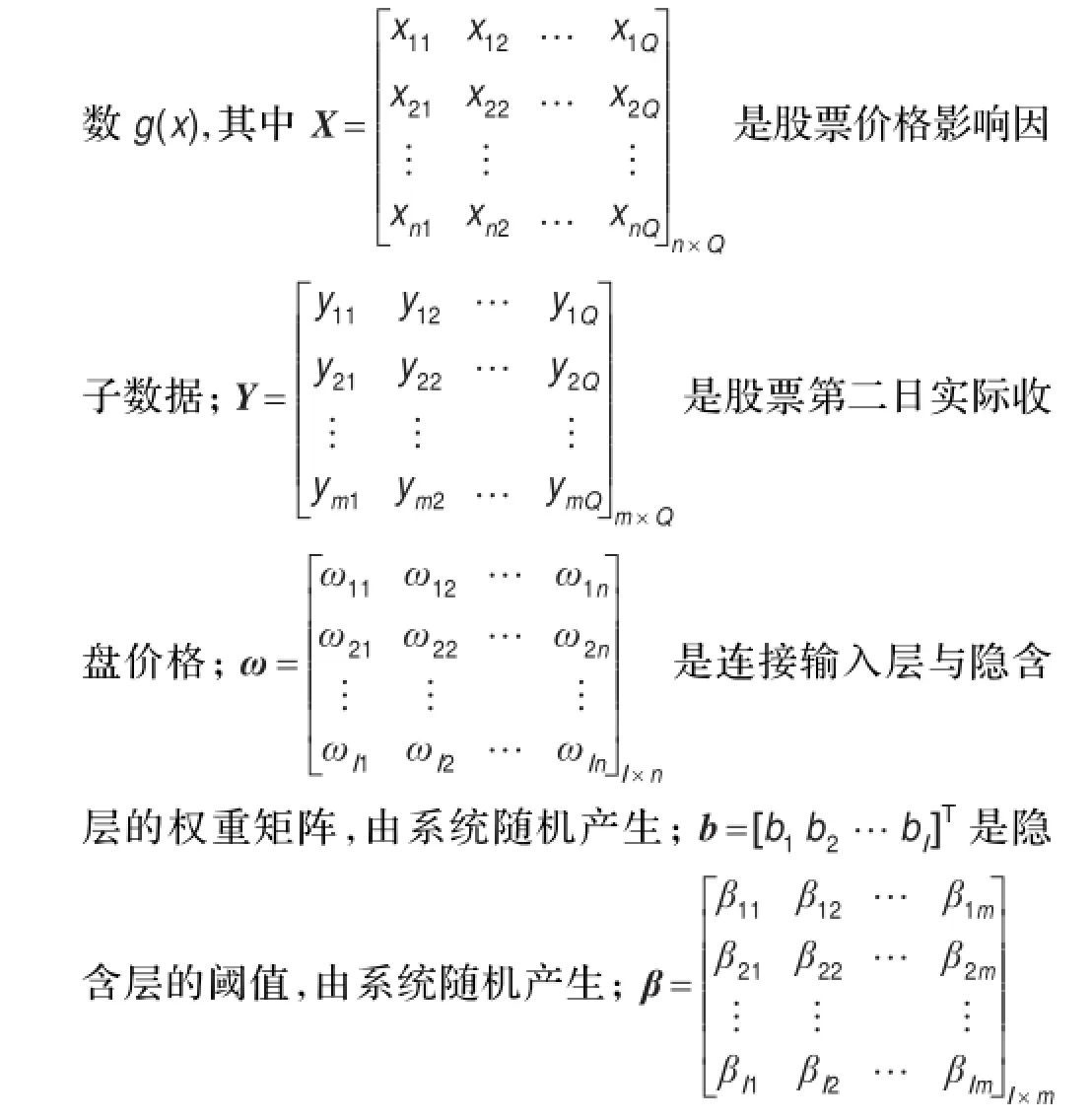
是连接隐含层和输出层的权重矩阵；则根据图1可知：

其中，H为隐含层神经网络的隐含层输出矩阵，具体形式见式（2），H+为隐含层输出矩阵H的Moore-Penrose广义逆。

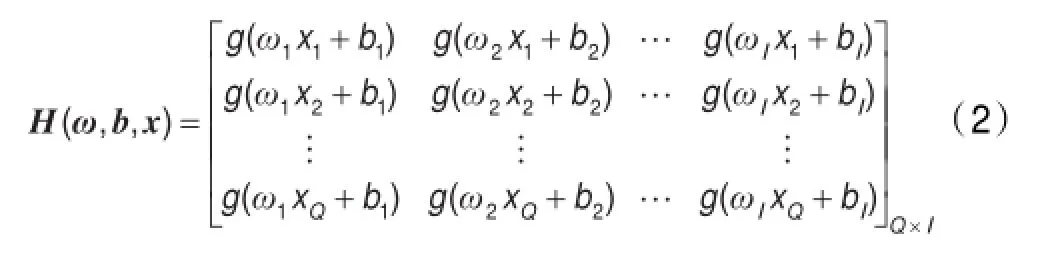
式中，ωi=[ωi1ωi2…ωin]，xj=[x1jx2j…xnj]T，g(x)为隐含层神经元激活函数。

根据以上分析可知，在ELM学习过程中，系统会随机产生输入层与隐含层权重矩阵ω和隐含层的阈值b，同时还需要人为指定隐含层神经元数量l，而这些参数将会影响到ELM学习效率以及未来预测模型的泛化能力和稳定性。因而，需要通过果蝇优化算法对这些参数加以优化，来增强ELM预测模型的泛化能力和稳定性。

3 改进果蝇优化算法

3.1 基本果蝇优化算法

果蝇优化算法（Fruit Fly of Algorithm，FOA）是一种基于果蝇觅食行为推演出的寻求全局优化的新方法。果蝇本身在感官知觉上优于其他物种，尤其是在嗅觉与视觉上。果蝇的嗅觉器官能很好地搜集飘浮在空气中的各种气味，然后飞近食物位置后亦可使用敏锐的视觉发现食物与同伴聚集的位置，并且往该方向飞去。依据果蝇搜索食物特性，将果蝇优化算法归纳为以下几个步骤[13-14]：

（1）给定群体规模SizePop，最大迭代数Maxgen，随机初始化果蝇群体位置x_axis、y_axis。

（2）赋予果蝇个体利用嗅觉搜寻食物之随机方向λ与群半径r，i次迭代寻优后果蝇群位置坐标为：

其中λ为[0,1]的随机数，i为迭代寻优次数。

（3）由于无法得知食物位置，因此先估计与原点之距离Disti，再计算味道浓度判定值Si，此值为距离之倒数：

（4）将味道浓度判定值Si代入味道浓度判定函数（或称为适应度函数Fitness function，用来求出果蝇个体位置的味道浓度Smell）。

（5）找出该果蝇群体中味道浓度最佳的果蝇（适用于最小化问题）：

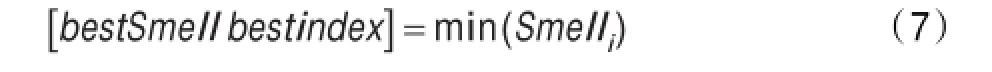
（6）记录并保留最佳味道浓度值bestSmell及其坐标(xbest，ybest)，此时果蝇群体中各个果蝇利用视觉向该位置飞去。

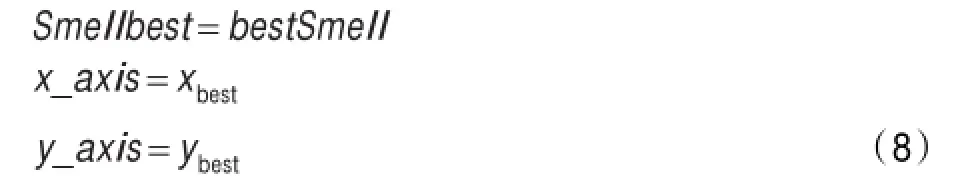
（7）进入迭代寻优，重复执行步骤（2）～（5），并判断最佳味道浓度是否优于前一迭代最佳味道浓度，并且当前迭代次数小于最大迭代数Maxgen，若是则执行步骤（6）。

3.2 改进的果蝇优化算法（Improved Fruit Fly of Algorithm，IFOA）

通过对基本的果蝇优化算法的分析可知，果蝇的搜索范围受到群半径r的限制，如果r值过大，则初期有利于使其在全局范围内搜索，但到迭代后期则可能出现算法错过最优解，从而使算法收敛速度慢或不能收敛；但是如果r过小，则会导致果蝇只能在局部区域搜索，无法跳出局部最优解。要克服这一问题，就必须提供一种机制，让算法既能在全局范围内寻找最优解，又能保证局部区域的搜索精度。

因此，本文提出了一种改进果蝇优化算法的方法，该方法针对群半径r提出这样一种机制，当迭代次数i为奇数时，则要求算法加强对全局范围内的搜索，也就是将r值设置为足够大的值；接着在其后的偶数次迭代时，则要求算法在当前搜索到的最优值附近区域内搜索更优值，即将r设置为足够小的值。通过如此循环，从而保证算法能够在全局范围内搜索到全局最优值。r值的确定方法见式（10），式中ΔSmellbest为每次最优值优化的幅度，i为当前迭代次数，Maxgen为最大迭代次数，并假设Maxgen为奇数。

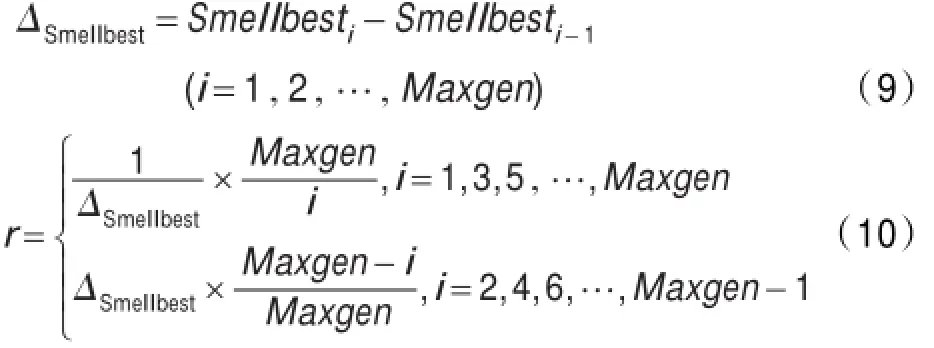
根据公式（10）可知，当i为奇数时，随着ΔSmellbest越来越小，算法陷入局部最优的可能性将越来越大，因此将1/ΔSmellbest作为r的一个因子。考虑到算法初始时可能出现ΔSmellbest值较大，从而可能导致r的搜索范围较小，因此加入Maxgen/i进行平衡。当i为偶数时，随着ΔSmellbest越来越小，算法要进一步加强对当前最优值附近区域的搜索，搜索范围应越来越小，因此将ΔSmellbest和(Maxgen-i)/Maxgen同时作为r的因子，从而保证当前区域内的搜索精度。

3.3 IFOA与FOA性能对比

为了验证本文提出的IFOA算法的性能，这里设计了两类实验：（1）FOA优化实验；（2）IFOA优化实验。实验中选用了2个优化算法比较基准函数，函数的形式、维数、理论极小值见表1所示。

为了比较IFOA与FOA算法的性能，本文在进行两类实验时，均选用相同的参数，具体参数设置为：群体规模SizePop=15，最大迭代数Maxgen=100；迭代的果蝇搜寻食物的随机飞行方向与距离区间为[-1，1]。性能评估采用两种算法运行20次的平均最优解的比较。具体比较结果见表2。

表1 用于测试改进算法的优化函数

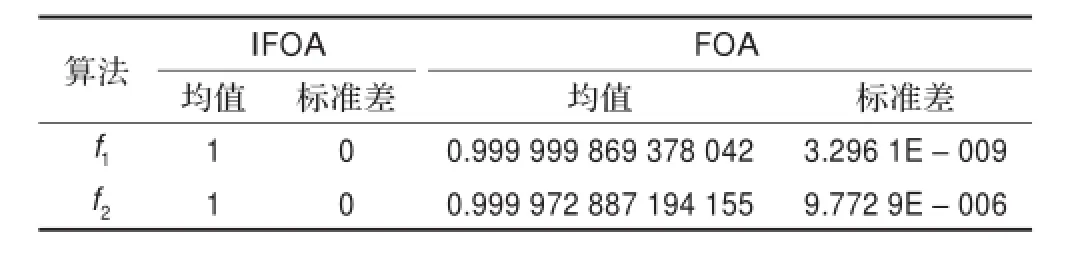
表2 各算法的平均最大值及其标准差

由表2的比较结果可知，本文提出的IFOA算法具有更好的全局与局部搜索能力，在收敛可靠性及收敛精度上较FOA算法有较大的提高。

4 改进果蝇优化算法优化极限学习机预测模型

将IFOA与ELM相结合，得到IFOA-ELM。IFOAELM主要思想是利用改进果蝇优化算法对ELM的输入层与隐含层连接权重矩阵ω和隐含层阈值b进行训练和优化，从而得到最优的ωbest和bbest，然后根据公式（1）计算得到βbest；接着将这些参数代入ELM预测模型进行预测。

步骤1果蝇优化算法的参数初始化，包括：群体规模SizePop，迭代次数Maxgen，初始位置x_axis、y_axis，当前全局最优值Smellbest0以及最优值优化幅度ΔSmellbest。

步骤2构建ELM网络拓扑结构，设置隐含层神经元初始值l，并设定隐含层神经元l的搜索区间[a，c][8]，通过设置隐含层神经元数量的上下限可以有效减少搜索区间的范围，提高搜索效率。

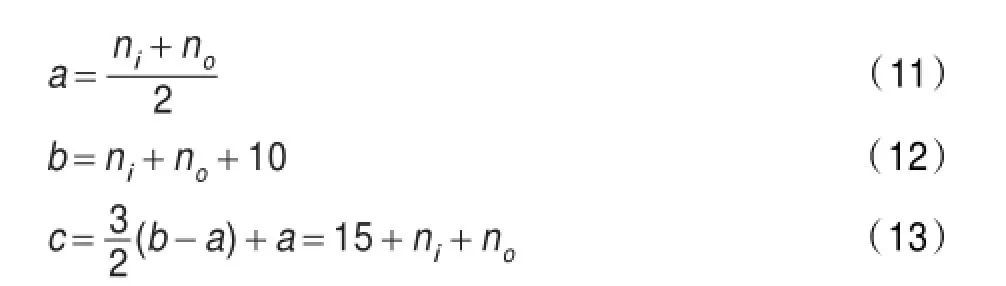
式中，ni和no分别为神经网络的输入层和输出层的神经元的数量。

步骤3根据优化对象“输入层与隐含层的连接权重矩阵ω”和“隐含层的阈值b”生成果蝇群，并随机初始化每只果蝇的位置和群半径。式中，S为果蝇的维数，ni为输入层神经元数量，l为隐含层神经元数量。

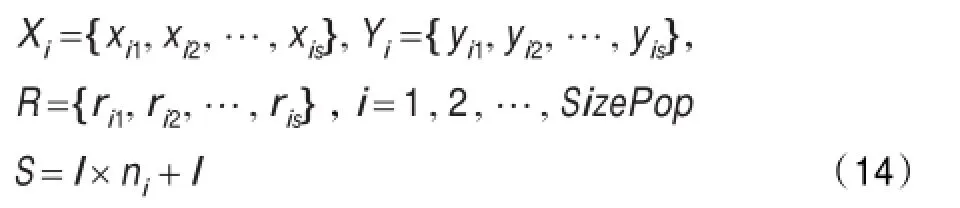
步骤4参照公式（4）、（5）计算味道浓度判定值Si。

步骤5计算果蝇个体位置的味道浓度，浓度判定函数是衡量果蝇个体位置优劣的标准，对于第i个果蝇的味道浓度表示为：

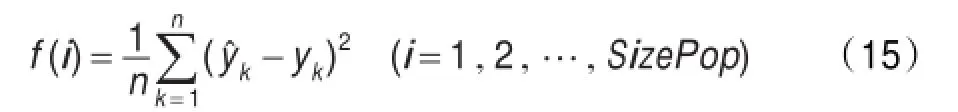
式中，n为训练样本数，SizePop为种群规模。

步骤6根据公式（7）找出该果蝇群体中味道浓度最佳的果蝇及其味道浓度值，并判断当前找到的味道浓度值是否优于全局最优值，如果优于则参照公式（9）更新ΔSmellbest；否则更新隐含层神经元数量值l=l+1，返回步骤3。

步骤7记录并保留最佳味道浓度值bestSmell及其坐标(xbest，ybest)，初始化果蝇种群位置为全局最优位置(xbest，ybest)，并根据公式（10）更新r。

步骤8当l值小于隐含层神经元数量的最大值c时，返回步骤3。否则退出果蝇优化，将得到的最优果蝇赋给ELM的输入层与隐含层的连接权重矩阵ω和隐含层的阈值b，ELM将根据这些参数对股票价格进行预测。

5 实验仿真

5.1 仿真环境

5.1.1 实验数据

本文选择在上海证券交易所上市的中国银行（601988）为实验对象，并将股票的开盘价、最高价、最低价、涨幅、振幅、总手、成交金额、换手、成交次数这9个指标作为预测模型的输入指标集，将股票第二日的收盘价作为输出指标。在数据区间选择上，本文选取从2012年8月13日到2013年7月1日之间的210个交易日数据，其中前200个工作日数据作为训练集，后10个工作日数据作为测试集。由于数据较多，这里只列出部分训练集和全部的测试集，数据见表3（数据来源于同花顺软件）。

5.1.2 实验数据预处理

在果蝇优化极限学习机的过程中，果蝇的维数S的增加将降低算法的执行效率。因此，需要对果蝇的维数S进行优化，从而提高果蝇优化算法的执行速度，减少算法执行所需的内存空间。由公式（14）可知，S的影响因子有两个，分别为输入层神经元数量ni和隐含层神经元数量l。由于隐含层神经元数量l无法事先确定，因此只能对ni进行优化。于是本文提出使用因子分析法对股票价格影响因子数据进行缩减，从而间接实现果蝇的维数S的减少，达到提高果蝇优化算法执行效率的目的。

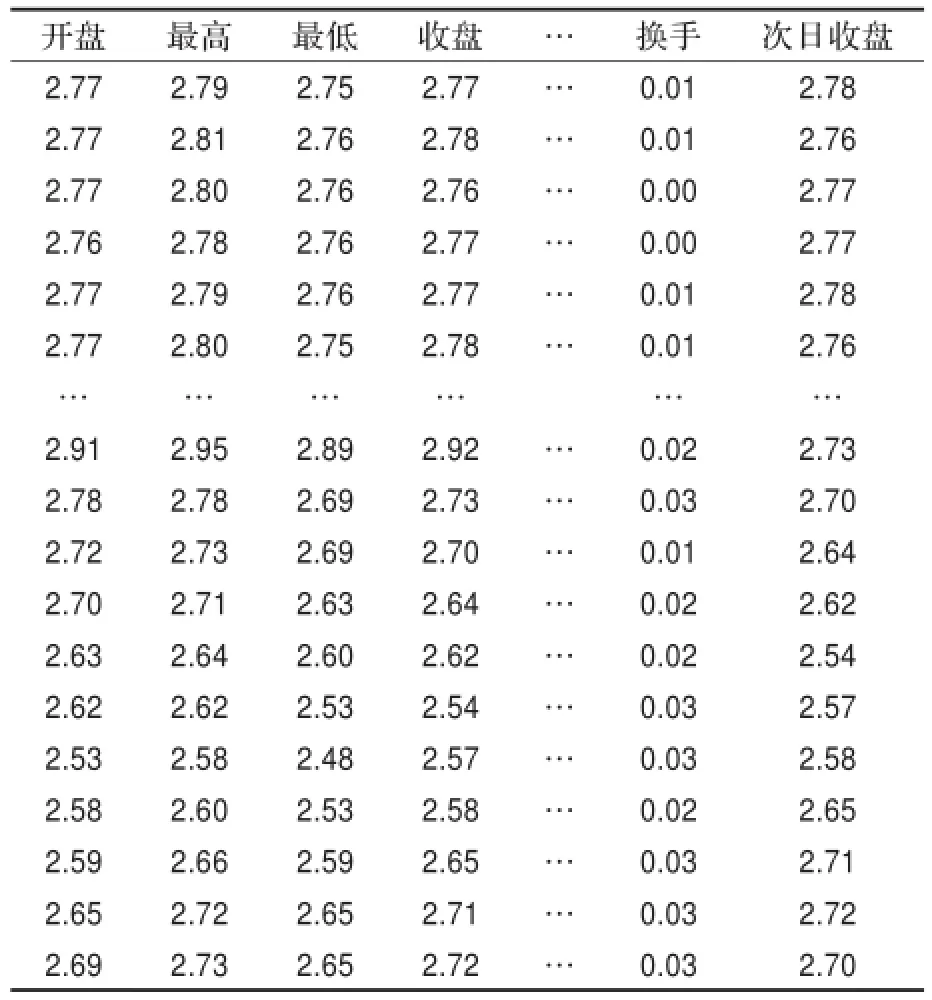
表3 中国银行股票成交信息表

为保证因子分析的效果，本文利用SPSS21.0工具提供的Bartlett球形检验和KMO对原始数据进行了因子分析检验。根据表4的检验结果可知，本文研究数据的KMO值为0.624>0.6，表示可以进行因子分析。同时，Bartlett球形检验的值为9 427.322（自由度为36），Sig.（显著性水平值）为0.000<0.05，达到了显著性水平，说明研究数据的相关变量之间有共同因素存在，适合进行因子分析。

表4 KMO和Bartlett的检验结果表

在构造因子变量过程中，本文采用映象分析法提取综合因子，并依据碎石图的结果选择5作为综合因子的提取数量，其累计方差贡献率达到99.925%；接着本文使用方差最大法对5个综合因子进行旋转，使每个变量在尽可能少的因子上有比较高的载荷；最后，本文使用Thomson回归法计算公共因子的因子得分，并将计算结果保存，作为未来ELM的输入数据。

5.1.3 参比模型与参数设置

在Matlab R2010b环境下，采用Matlab语言编写算法程序，构建三种预测模型，分别为：ELM模型、FOAELM模型和IFOA-ELM模型。

ELM模型参数设置：隐含层神经元数量为6，隐含层神经元激活函数选用sigmoid函数。

FOA-ELM模型参数设置：ELM的隐含层神经元数量的搜索范围[15]为隐含层神经元激活函数选用sigmoid函数。FOA的参数设置：种群规模为100，迭代次数为100。

IFOA-ELM模型中，各参数设置同FOA-ELM。

5.2 仿真结果

将上述数据经因子分析后，分别用ELM、FOA-ELM和IFOA-ELM模型进行预测，得到仿真图如图2所示。

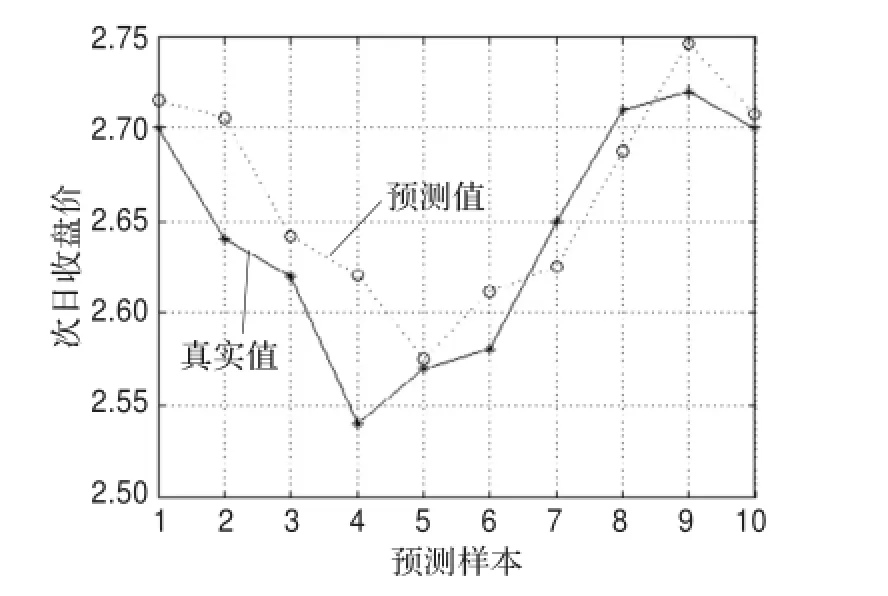
图2 IFOA-ELM模型预测图（mse=0.001 438 8）

根据IFOA-ELM模型得到的预测结果如图2所示，图中用“*”画出的曲线代表真实数据，用“○”画出的曲线代表预测值。从图2可以看到，IFOA-ELM模型预测的总体趋势和实际股票价格的走势基本一致，且误差较小，预测效果较好。

为了进一步验证本文提出模型的优劣性，使用ELM和FOA-ELM作为参比模型，各模型对比结果见图3、图4和表5。

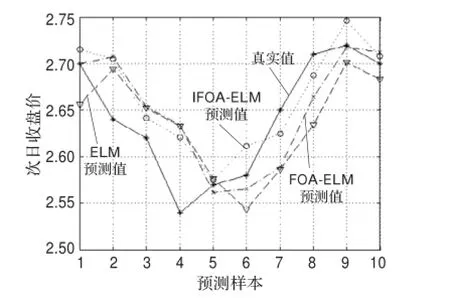
图3 多模型预测值比较图

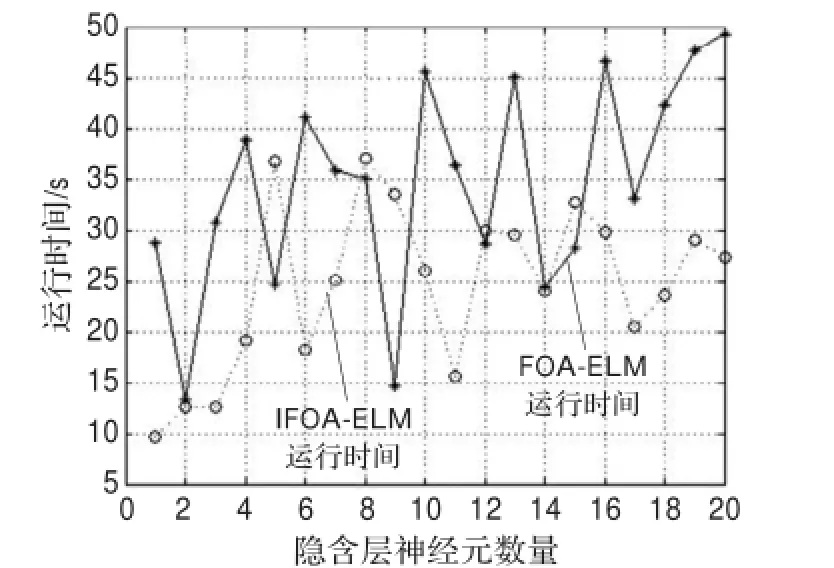
图4 多模型训练时间对比图

由图3和表5可知，本文提出的IFOA-ELM模型的预测结果是所有参比模型中精度最高者，其预测值与实际值最为接近。通过对各模型预测精度对比可以发现，ELM的预测精度最低，FOA-ELM的预测精度高于ELM，IFOA-ELM的预测精度又显著高于FOA-ELM。在训练时间上，由于ELM模型没有参数优化过程，因此这里重点对比FOA-ELM模型和IFOA-ELM模型。由图4及表5可知，IFOA-ELM模型的训练时间明显少于FOA-ELM，究其原因，主要是因为IFOA-ELM的收敛速度快，减少了最优值的替代次数，从而减少了预测模型的训练时间。通过以上讨论，可以发现IFOA-ELM是一个有效的、高精度的、高效率的股价预测模型。

表5 各模型运行结果对比表

6 结论

本文通过提出IFOA-ELM算法，来解决极限学习机预测模型稳定性不理想的问题。相比基本的FOA算法，IFOA算法收敛速度快，增加了后期跳出局部最优的可能性，有利于找到全局最优解。文中使用IFOA-ELM预测模型对中国银行（601988）2013年6月19日到2013年7月2日的收盘价格进行了预测，与ELM预测模型和FOA-ELM预测模型相比，该方法提高了模型的预测精度和训练速度，降低了FOA-ELM预测模型陷入局部极小的可能性。

[1]Zhang Yudong，Wu Lenan.Stock market prediction of S&P 500 via combination of improved BCO approach and BP neural network[J].Expert Systems with Applications，2009，36（5）：8849-8854.

[2]Vanstone B，Finnie G.An empirical methodology for developing stock market trading systems using artificial neural networks[J].Expert Systems with Applications，2009，36（3）：6668-6680.

[3]郝华宁，刘阳.基于遗传神经网络的个股价格短期预测[J].西安石油大学学报：自然科学版，2010（2）.

[4]郑斯日古楞.灰色神经网络在股票价格预测中的应用[J].计算机仿真，2012（2）：392-395.

[5]Huang G B，Zhu Q Y，Siew C K.Extreme learning machine：a new learning scheme of feedforward neural networks[C]// 2004 International Joint Conference on Neural Networks，Budapest，Hungar，2004：958-990.

[6]Huang G B，Zhu Q Y，Siew C K.Extreme learning machine：theory and applications[J].Neurocomputing，2006，70（1/3）：489-501.

[7]高光勇，蒋国平.采用优化极限学习机的多变量混沌时间序列预测[J].物理学报，2012，61（4）：37-45.

[8]Suresh S，Babu R V，Kim H J.No-reference image quality assessment using modified extreme learning machine classifier[J].Applied Soft Computing，2009（2）：541-552.

[9]Huang G B，Chen L，Siew C K.Universal approximation using incremental feedforward networks with arbitrary input weights[J].Neural Networks，2006，17（4）：879-892.

[10]Lan Yuan，Yeng C S，Huang Guangbin.Ensemble of online sequential extreme learning machine[J].Neurocomputing，2009，72（1）：3391-3395.

[11]刘学艺，李平，郜传厚.极限学习机的快速留一交叉验证算法[J].上海交通大学学报，2011，45（8）：1140-1145.

[12]陆慧娟，安春霖，马小平，等.基于输出不一致测度的极限学习机集成的基因表达数据分类[J].计算机学报，2013（2）：341-348.

[13]Pan Wentsao.A new fruit fly optimization algorithm：taking the financial distress model as an example[J]. Knowledge-based Systems，2012，26：69-74.

[14]Pan Wentsao.A new evolutionary computation approach：fruit fly optimization algorithm[C]//Proc of the 11th Conference on Digital Technology and Innovation Management，2011.

[15]夏克文，李昌彪，沈钧毅.前向神经网络隐含层节点数的一种优化算法[J].计算机科学，2005（10）：143-145.

LI Dong,ZHANG Wenyu

School of Management Engineering,Xi’an University of Posts and Telecommunications,Xi’an 710061,China

Extreme Learning Machine（ELM）is not stable in predicting stock price.To address the problem,this paper proposes an Improved Fruit Fly of Algorithm（IFOA）that optimizes ELM by improving fruit fly.In the algorithm,fruit fly swarm constantly adjusts its radius to optimize the ELM input weights and thresholds of hidden layer,building an ELM prediction model with the optimized results.The IFOA-ELM model proposed in this paper can be applied to predicting stock price.Compared with ELM and FOA-ELM,IFOA-ELM model is more accurate and stable in predicting stock price.

stock price;prediction;Fruit Fly of Algorithm（FOA）;Extreme Learning Machine（ELM）

针对股票价格预测中应用极限学习机预测存在稳定性不理想的问题，提出了一种改进果蝇优化极限学习机（IFOA-ELM）预测模型的算法。在该算法中，果蝇群通过不断调整群半径来优化ELM的输入层与隐含层连接权值和隐含层阈值，并以优化后的结果为基础，构建ELM预测模型。将IFOA-ELM模型用于股票价格预测。实验表明，与ELM和FOA-ELM相比，IFOA-ELM在股票价格预测中具有更高的预测精度和更好的稳定性。

股票价格；预测；果蝇优化算法；极限学习机

A

TP183

10.3778/j.issn.1002-8331.1401-0037

LI Dong,ZHANG Wenyu.Stock price prediction based on ELM and FOA.Computer Engineering and Applications,2014,50（18）：14-18.

陕西省自然科学基金（No.2012GQ8050）；陕西省教育厅专项科研计划项目（No.13JK0403）；西安邮电大学中青年基金（No.104-0410）。

李栋（1981—），男，在读博士生，讲师，研究领域为数据挖掘；张文宇（1973—），女，博士，教授，研究领域为智能决策、数据挖掘、知识发现。E-mail：ddli1009@126.com

2014-01-06

2014-03-14

1002-8331（2014）18-0014-05

CNKI网络优先出版：2014-03-19，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1401-0037.html