三阶柯西差分方程在几类群上的解
杨林晓,赵侯宇
(重庆师范大学数学学院,重庆401331)
三阶柯西差分方程在几类群上的解
杨林晓,赵侯宇
(重庆师范大学数学学院,重庆401331)
在几类群上讨论了三阶柯西差分方程解的存在性问题,将二阶柯西差分方程的已有结论进一步推广到三阶的情况,并给出在不同群上的一般解.
函数方程;群;柯西差分
1 引言与预备知识
设(G,…)是一个群,(H,+)是一个交换群,e∈G和0∈H分别表示群G和群H上的单位元.若映射f:G→H,则f的柯西差分为C(m)f定义为:
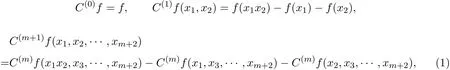
其中一阶柯西差分C(1)f简写为Cf.
关于柯西差分方程的讨论已有许多结果[1-7],文献[7]中,作者讨论了二阶柯西差分方程在群上的解,本文在此基础上进一步考虑方程:
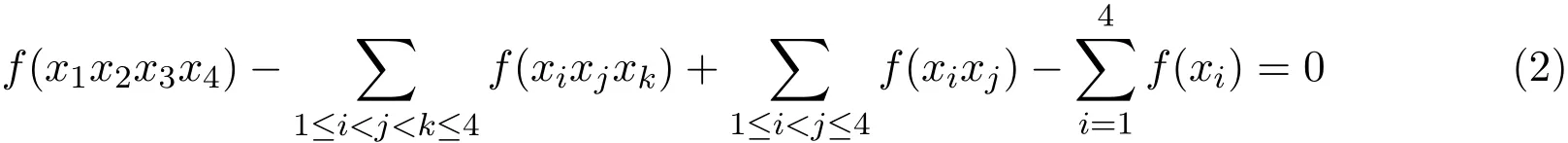
在几类群上的解.其中xi∈G,i=1,2,3,4.事实上,此方程等价于f的三阶柯西差分方程,即C(3)f=0.(2)式的一般解可用下式表示:
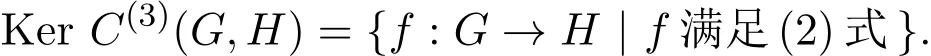
且有
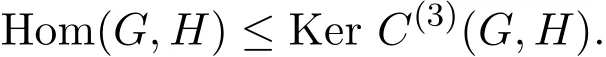
类似于文献[7],有如下两个引理,此处省略其证明过程.
引理1.1设(G,…)是一个群,(H,+)是一个交换群,且f:G→H.若f满足(2)式,则有以下结论成立:
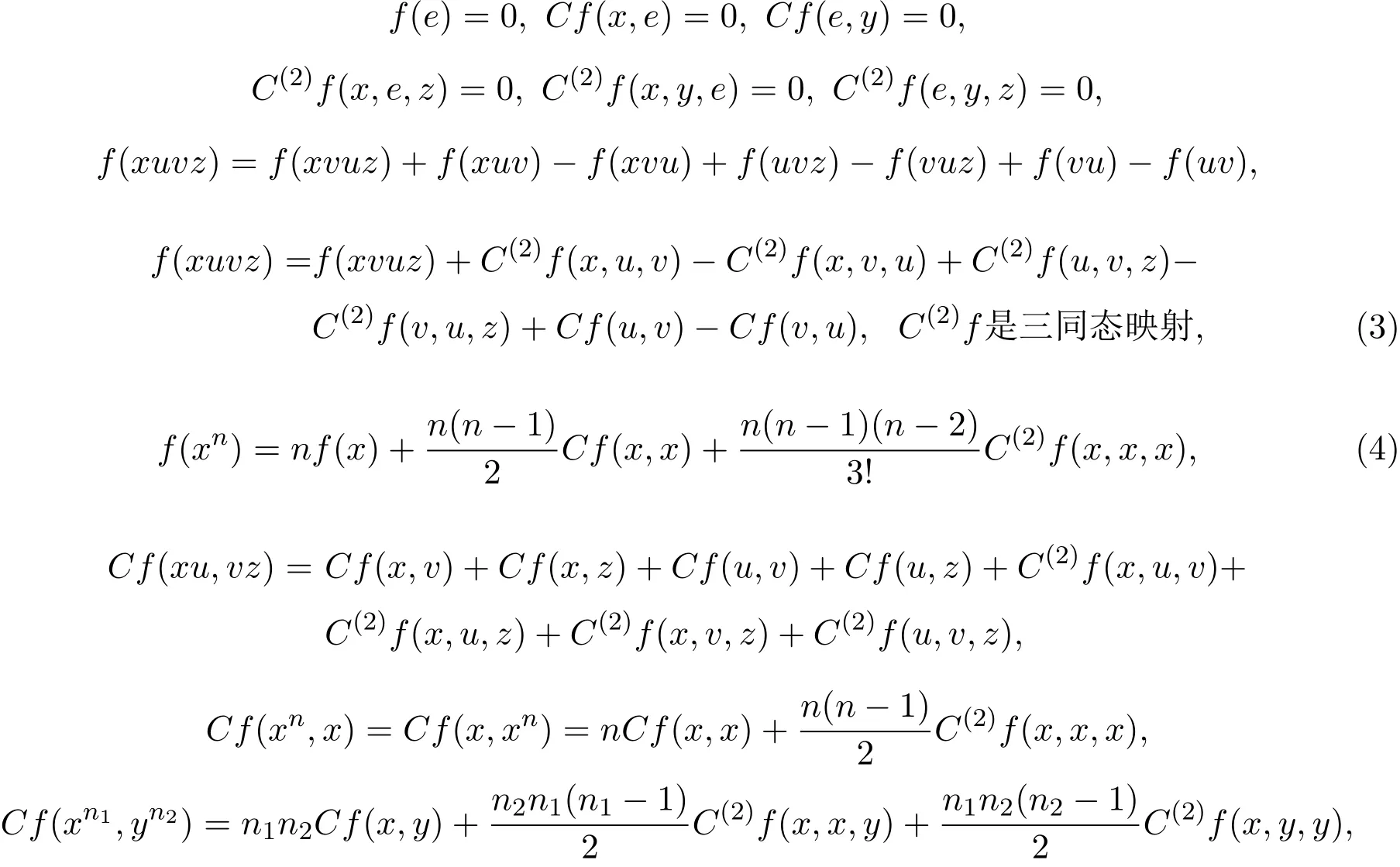
其中∀x,y,z,µ,ν∈G,n,n1,n2∈
注1.1方程(4)来源于C(3)f=0,由(1)式可知C(2)f(…,y,z)是一个态射,C(2)f对于它的第二个元素和第三个元素同样也是一个态射,即从C(2)f的定义中也可推出(3)式.
下面等式∀f:G→H均成立:
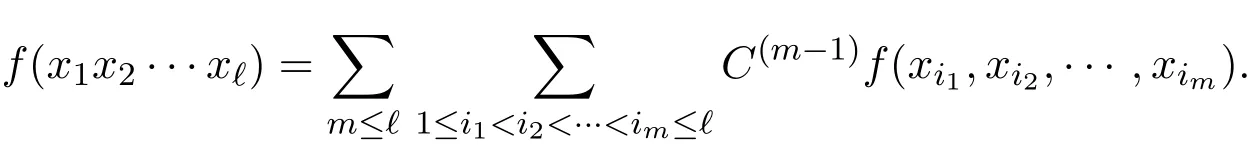
引理1.2如果f∈Ker C(3)(G,H),则
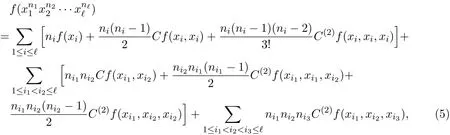
其中xi∈G和ni∈,i=1,2,………,l.该引理的证明类似于文献[2],故省略此处证明.
注1.2上述引理是(4)式的推广,如果在(5)式中令l=2,x1=x2=x,则由(5)式可得到(4)式,此时n=n1+n2.事实上,
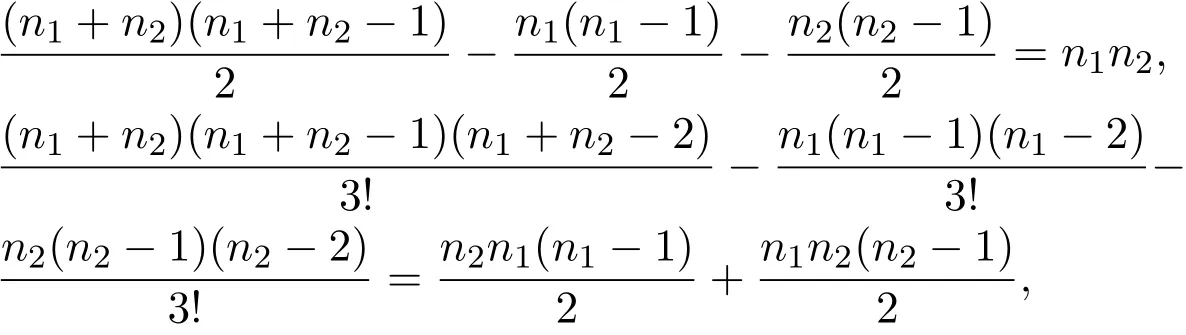
其中∀n1,n2∈.
2 方程(2)在n阶对称群Sn上的解
考虑方程(2)在G=Sn时的情况.此时,当n=1和n=2的情形是平凡的,不妨设n≥3.若f∈Ker C(3)(G,H),由(3)式知C(2)f是三态射,且H是一个交换群,因此
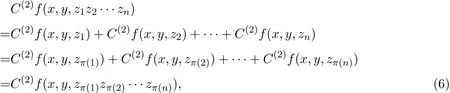
其中∀x,y,zi∈Sn,π是任意一个n级排列.类似地有,
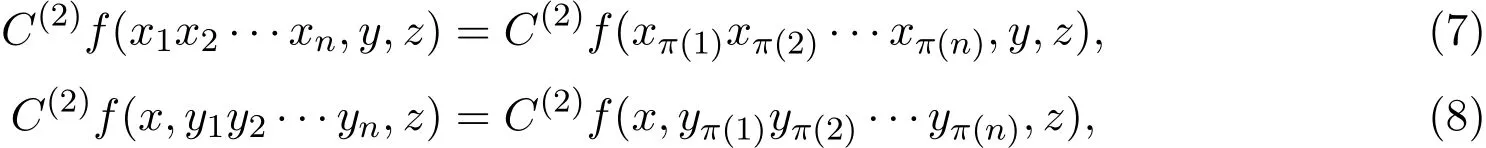
其中∀x,y,z,xi,yi∈Sn,π是任意一个n级排列.
设σ是任意的一个n阶对称群Sn上的2-循环(即一个对换).由Cf的定义并利用σ2=e和引理1.1可得,
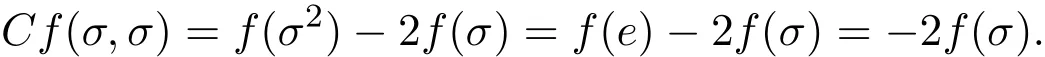
而且,利用σ4=e,σ3=σ,及(1)式得
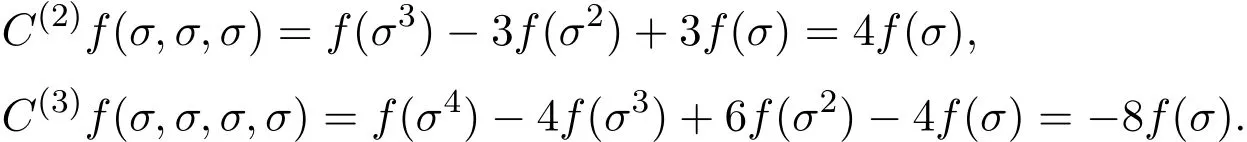
由于C(3)f=0,得

对于2-循环σ,∃z∈Sn使得σ和2-循环(1 2)满足:σ=z(1 2)z−1.∀x,y∈Sn,由(6)式有
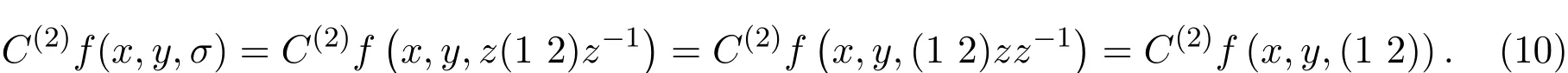
类似地,利用(7)式和(8)式,∀2-循环τ,π和∀x,y,z∈Sn,可得,
结合(10)-(12)式,得
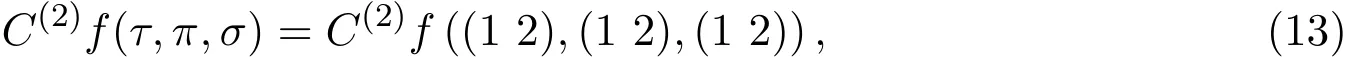
其中∀2-循环σ,τ,π∈Sn.而
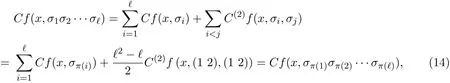
其中∀x,2-循环σi∈Sn,π是任意的n级排列.
类似地,可得

其中∀y,2-循环τi∈Sn,π是任意的n级排列.∀2-循环σ,τ∈Sn,由(14),(15)式有
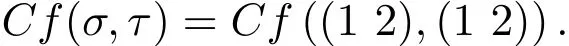
因此可得,
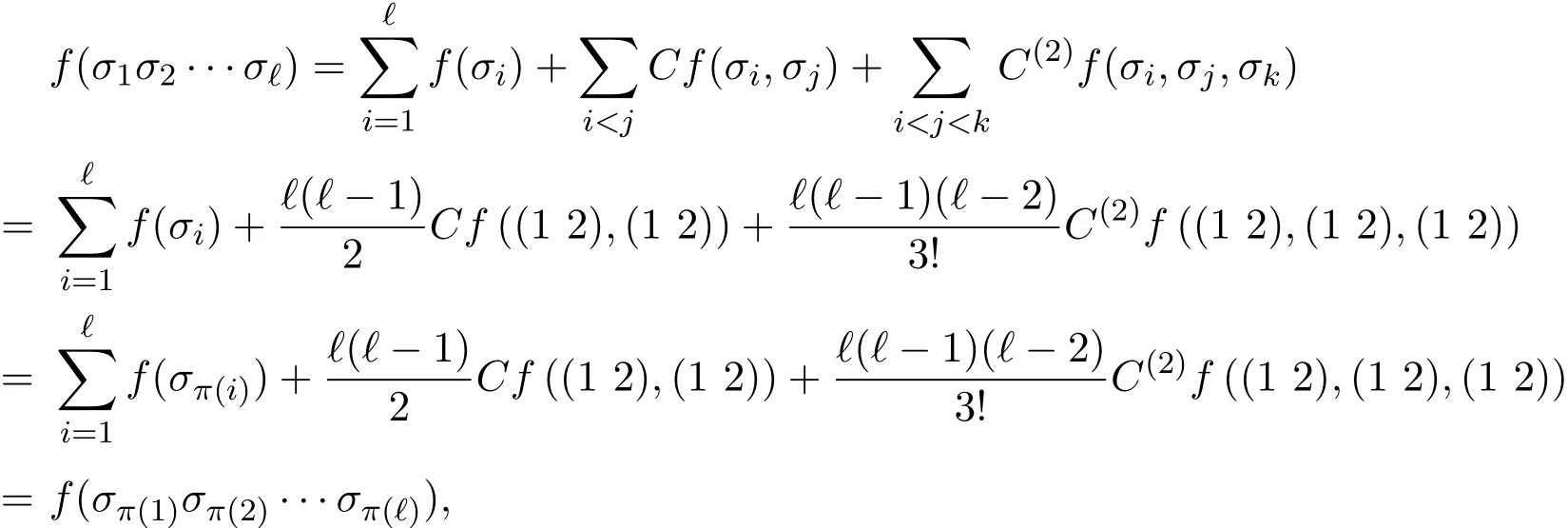
其中2-循环σi∈Sn,π是任意的n级排列.
引理2.1[7]对任意的x,y,β∈Sn,其中β是一个2-循环,则

特别地,在(16)式中令x=y=e,有f(β)=f((1 2)),其中2-循环β∈Sn.
下面求(2)式在群Sn上的解.
定理2.1f∈Ker C(3)(Sn,H)当且仅当f满足下式:

其中h0∈H是一个常数且满足8h0=0.
证明设f∈Ker C(3)(Sn,H).设x∈Sn,则存在2-循环αi∈Sn,i=1,………,p,使得x=α1α2………αp.故

由(9)式,得8f((1 2))=0.因此由(18)式可推出

令h0:=f((1 2)),这就证明了f一定满足(17)式.相反的,设f:Sn→H,满足(17)式,其中h0∈H是一个常数且满足8h0=0.易证f满足(2)式.证毕.
注2.1如果p是偶数,则
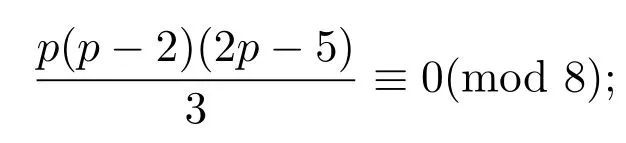
如果p是奇数,则
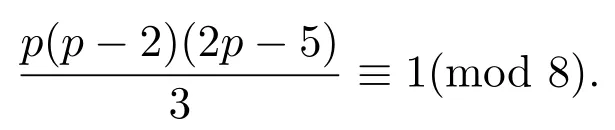
3 方程(2)在有限循环群Gn上的解
设Gn=〈a|an=e〉是由元a生成的n阶有限循环群.
定理3.1设f:Gn→H是方程(2)的一般解,则
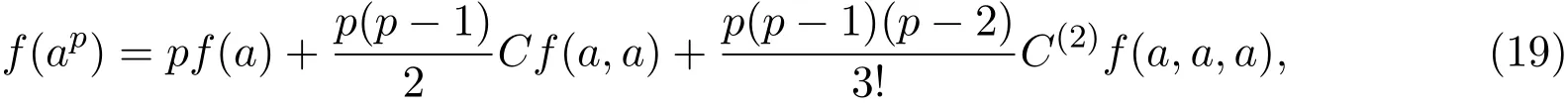
其中∀p∈Z,f(a),Cf(a,a),C(2)f(a,a,a)是群H上的常数且满足:
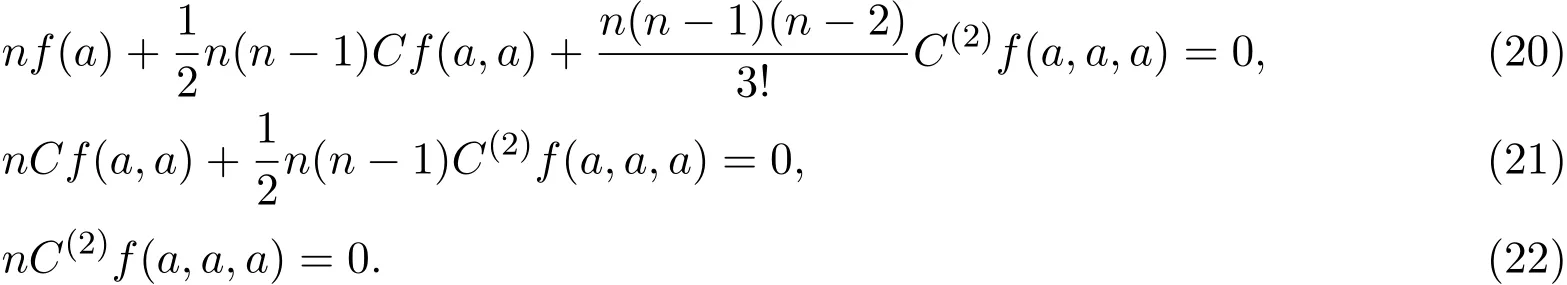
证明设f:Gn→H满足方程(2).则由(4)式得,f满足(19)式:
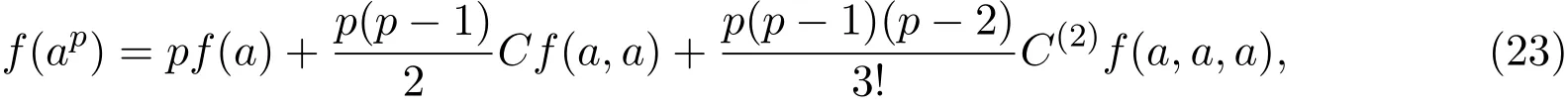
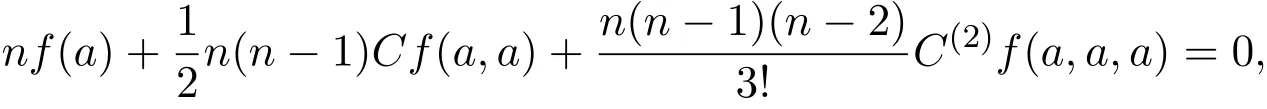
又因为an=e,由引理1.1,得
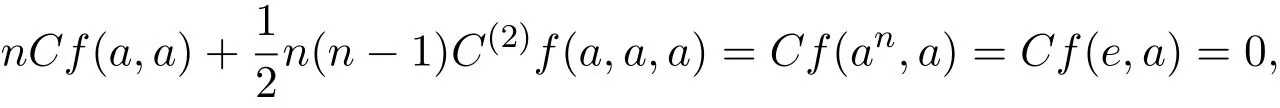
及
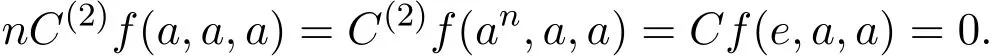
这就证明了(20)-(22)式.
反之,设f:Gn→H由(19)式定义,其中f(a),Cf(a,a),C(2)f(a,a,a)是群H上的常数且满足(20)-(22)式,故有f是定义在群Gn上的.由(20)-(22)式知,
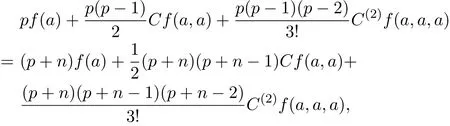
即f(ap)=f(ap+n).
∀x1=ak,x2=al,x3=am,x4=an∈Gn,易证
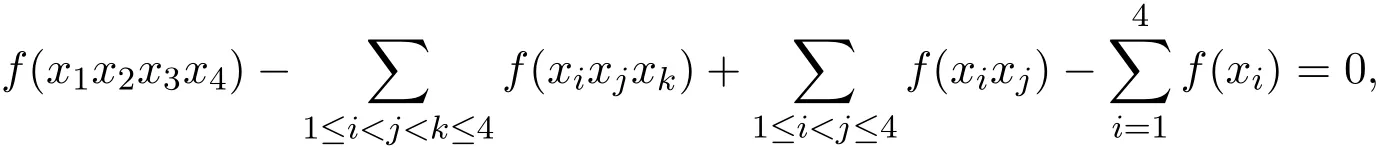
故f满足方程(2).定理得证.
4 方程(2)在二面体群Dn上的解
设Dn=〈a,b|an=e,b2=e,abab=e〉是2n(n≥2)阶二面体群.
定理4.1设f:Dn→H是方程(2)的一般解,则f满足以下形式:
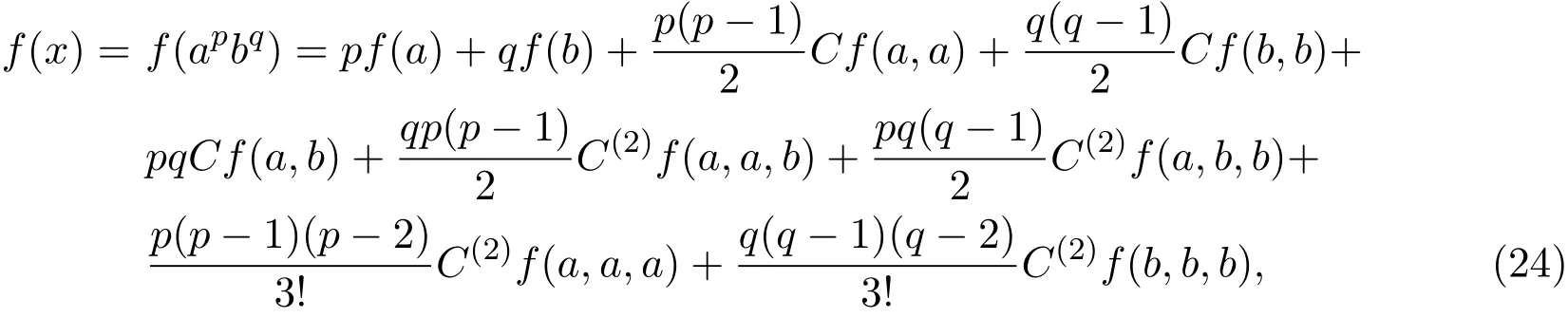
∀p,q∈Z,f(a),f(b),Cf(a,a),Cf(b,b),Cf(a,b),C(2)f(a,a,a),C(2)f(b,b,b),C(2)f(a,a,b)和C(2)f(a,b,b)是群H上的常数,且满足:
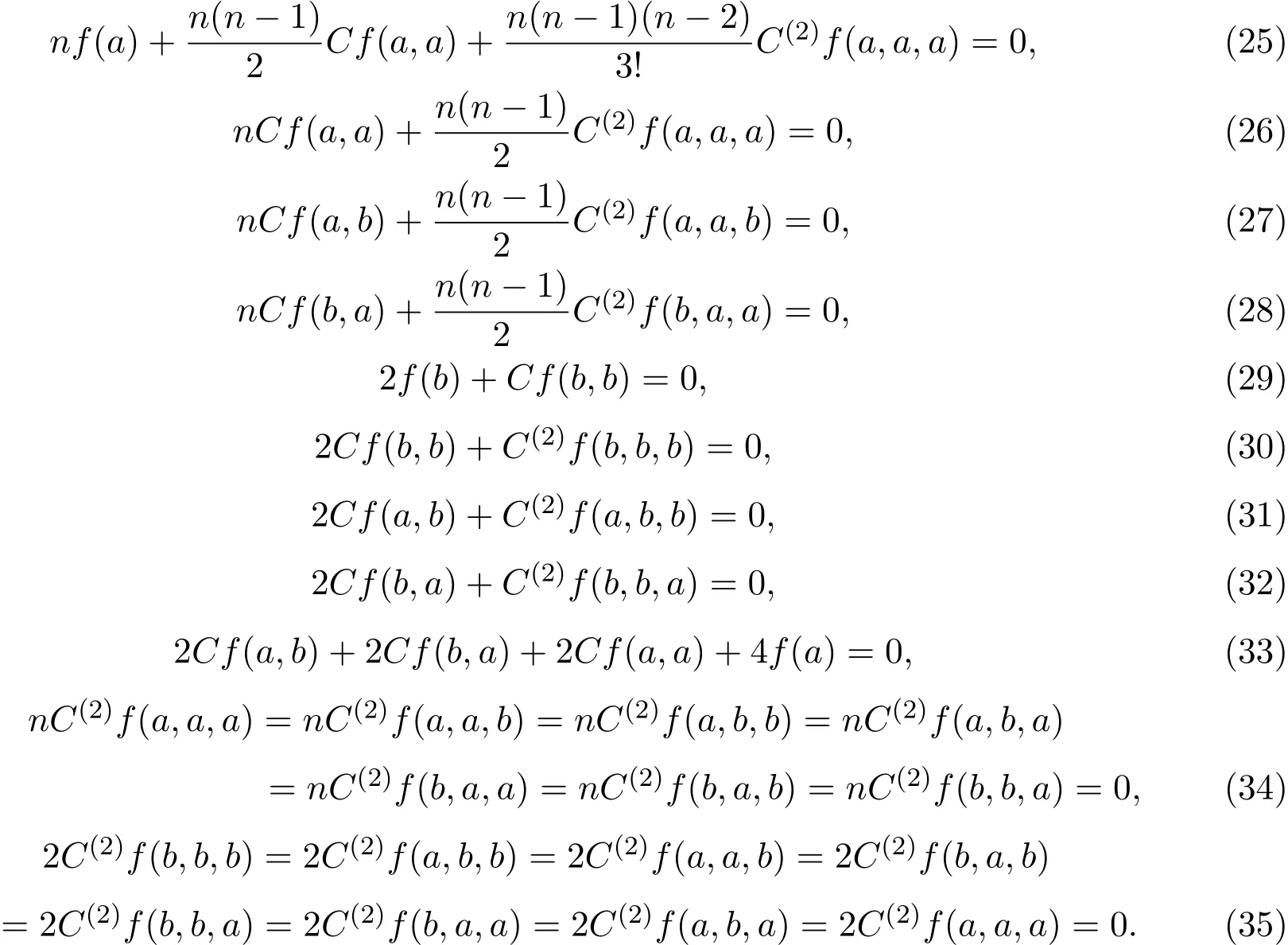
注4.1由上述等式可推出8f(a)=8f(b)=0.由(25)-(35)式,有
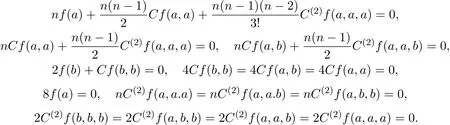
证明设f:Dn→H满足(2)式.由引理1.2可知
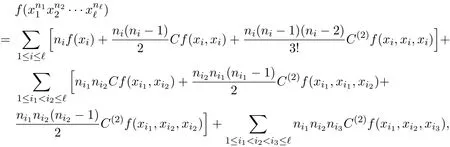
其中xi∈{a,b}.特别地,令x1=a,x2=b,ℓ=2,可得(24)式.
由引理1.1知,对每个群Dn中由a,b生成的满足w=e的元有,
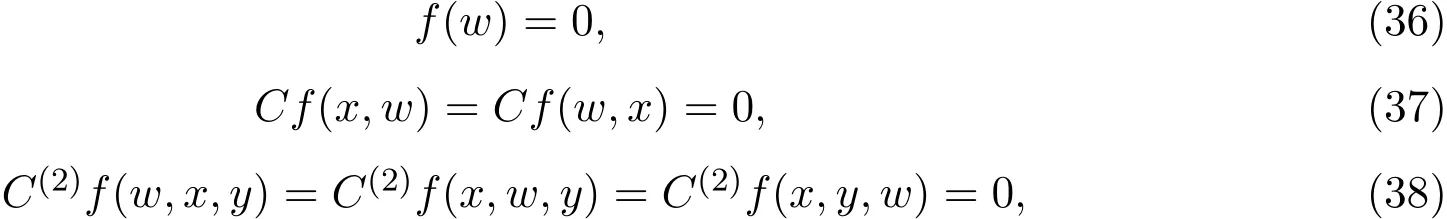
∀x和y∈Dn.因为a,b是Dn的生成元,(37)式对于所有的x成立当且仅当x=a和x=b时(37)式也成立:
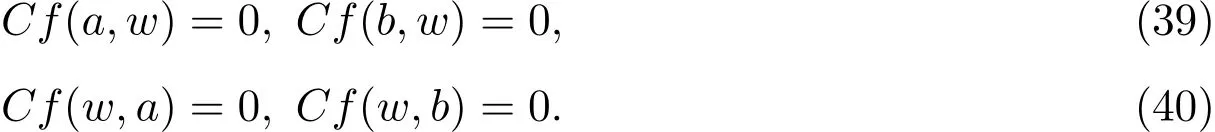
又因为C(2)f是一个三态射,a和b是Dn的生成元,(38)式对于所有的x,y成立当且仅当x=a,y=a;x=a,y=b;x=b,y=a;x=b,y=b这四种情形时(38)式也成立:
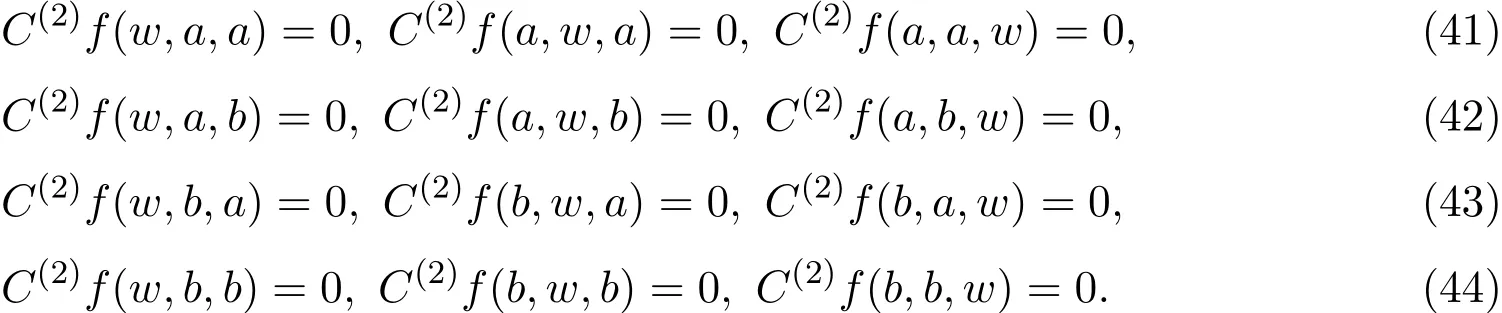
由群Dn的定义,在(36),(39)-(44)式中分别令w=an,w=b2和w=abab,可推出(25)-(35)式.
反之,设f:Dn→H由(24)式定义,其中f(a),f(b),Cf(a,a),Cf(b,b),Cf(a,b), C(2)f(a,a,a),C(2)f(b,b,b),C(2)f(a,a,b)和C(2)f(a,b,b)是群H上的常数,且满足(25)-(35)式.可直接验证(36)-(38)式.这就完成了证明.
注4.2在(24)式中,如果q是偶数,结合(25)-(35)式,有
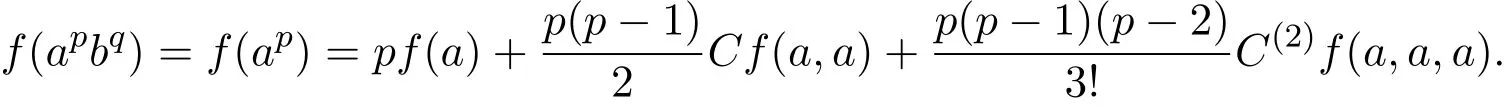
如果q是奇数
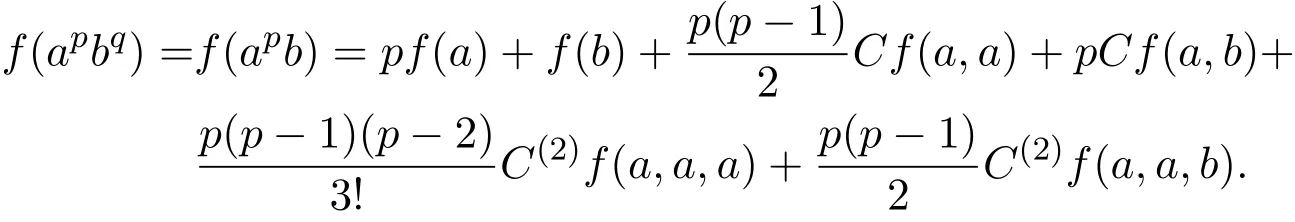
[1]Aczel J,Chung J K,Ng C T.Symmetric Second Di ff erences in Product Form on Groups[M].Singapore: World Scienti fi c Publ.Co.,1989.
[2]Baron K,Kannappan P L.On the Cauchy di ff erence[J].Aequationes Math.,1993,46:112-118.
[3]Ebanks B.Generalized Cauchy di ff erence functional equations[J].Aequationes Math.,2005,70:154-176.
[4]Ebanks B.Generalized Cauchy di ff erence equations,II[J].Proc Amer.Math.Soc.,2008,136(11):3911-3919.
[5]Heuvers K J.A characterization of Cauchy kernels[J].Aequationes Math.,1990,40:281-306.
[6]Heuvers K J.Another logarithmic functional equation[J].Aequationes Math.,1999,58:260-264.
[7]Ng C T,Zhao H Y.Kernel of the second order Cauchy di ff erence on groups[J].Aequationes Math., 2013,86:155-170.
Kernel of the third order Cauchy di ff erence on several groups
Yang Linxiao,Zhao Houyu
(School of Mathematics,Chongqing Normal University,Chongqing401331,China)
In this paper,we study the existence of solutions of third order Cauchy di ff erence on several groups, extend and improve some recent results to third order Cauchy di ff erence equation,and present its general solution on these groups.
functional equation,group,Cauchy di ff erence
O151
A
1008-5513(2014)03-0314-09
10.3969/j.issn.1008-5513.2014.03.014
2013-12-09.
国家自然科学基金(11326120);重庆师范大学自然科学基金(12XLZ04);重庆高校创新团队建设计划资助项目(KJTD201308).
杨林晓(1988-),硕士生,研究方向:微分方程与动力系统.
赵侯宇(1982-),博士,讲师,研究方向:微分方程与动力系统.
2010 MSC:39B52,39A70

