一类高阶变系数线性非齐次微分方程的解
贾庆菊
(山西财经大学应用数学学院,山西太原030006)
一类高阶变系数线性非齐次微分方程的解
贾庆菊
(山西财经大学应用数学学院,山西太原030006)
利用高阶变系数之间的关系,通过适当的线性变换,得到了五阶变系数线性非齐次方程常系数化的条件,给出了一类高阶变系数线性非齐次微分方程的新解法.
高阶;变系数线性非齐次微分方程;线性变换;常系数线性非齐次微分方程
1 引言
线性微分方程在科学研究、工程技术中有着广泛的应用.常系数线性微分方程,利用特征方程和常数变易法,求解问题已经彻底解决.但在生产实践以及经济领域中,人们常会遇到二阶或更高阶变系数线性微分方程.因此,探讨它们的解法具有重要理论意义和使用价值.这类方程虽然在理论上证明了解的存在性,但在实际求解中并不如意,尤其是高阶变系数线性非齐次微分方程没有一般的解法.为了满足理论研究和工程实践的需要,人们用不同的方法不断扩大变系数线性微分方程的可积类型,取得了不少成果.文献[1-3]讨论二阶变系数线性方程求解;文献[4-5]利用首次积分或变量代换将高阶微分方程化为可求解的微分方程,求解的基本原则是降阶的;文献[6-8]仅讨论了二阶变系数线性齐次方程常系数化问题.受著名的欧拉(Euler)方程的启发,试图寻找一种新的求解高阶变系数线性非齐次方程方法.那么,高阶变系数线性非齐次方程能否常系数化?常系数化的条件又是什么?本文借助高阶变系数之间的关系,通过适当的变量替换,将一类高阶变系数线性非齐次微分方程化为高阶常系数线性非齐次微分方程求解.
2 主要结果及证明
定理1五阶变系数线性非齐次微分方程:
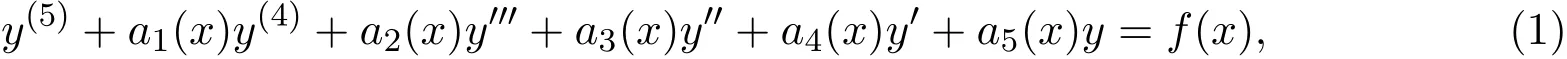
当系数满足:
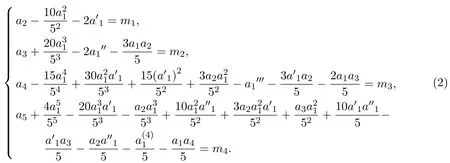
其中,mi(i=1,2,3,4)为常数.可通过变换

将(1)式化为五阶常系数线性非齐次微分方程求解.
证明令则
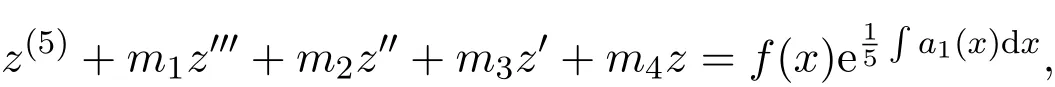
求出通解回代原来变量可得原方程通解.
定理2四阶变系数线性非齐次微分方程:
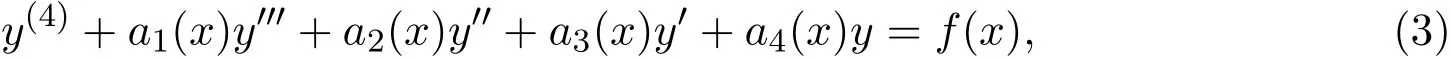
当系数满足:
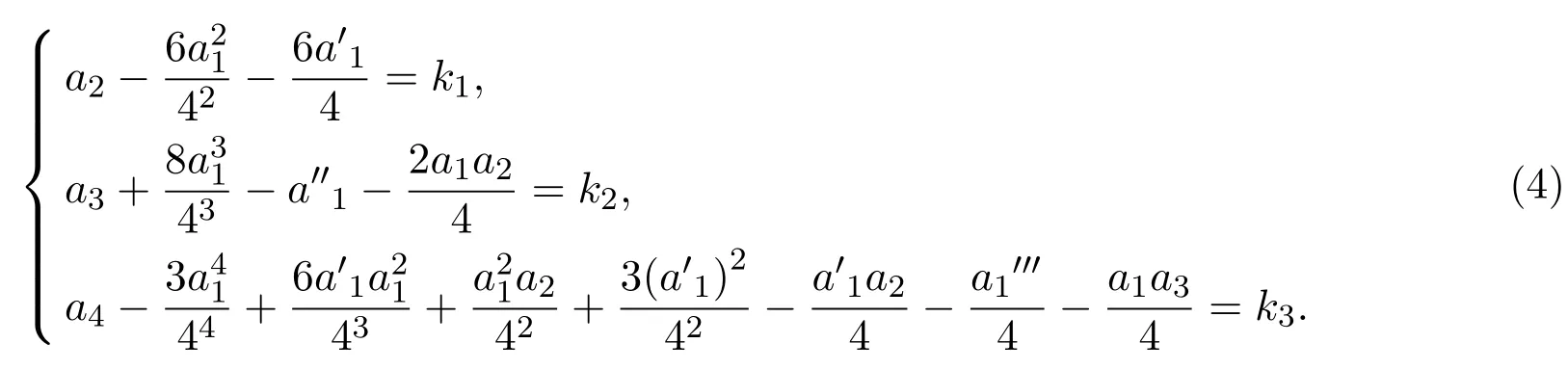
其中,ki(i=1,2,3)为常数.可通过变换
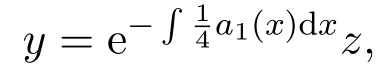
将(3)式化为四阶常系数线性非齐次微分求解.
证明令则
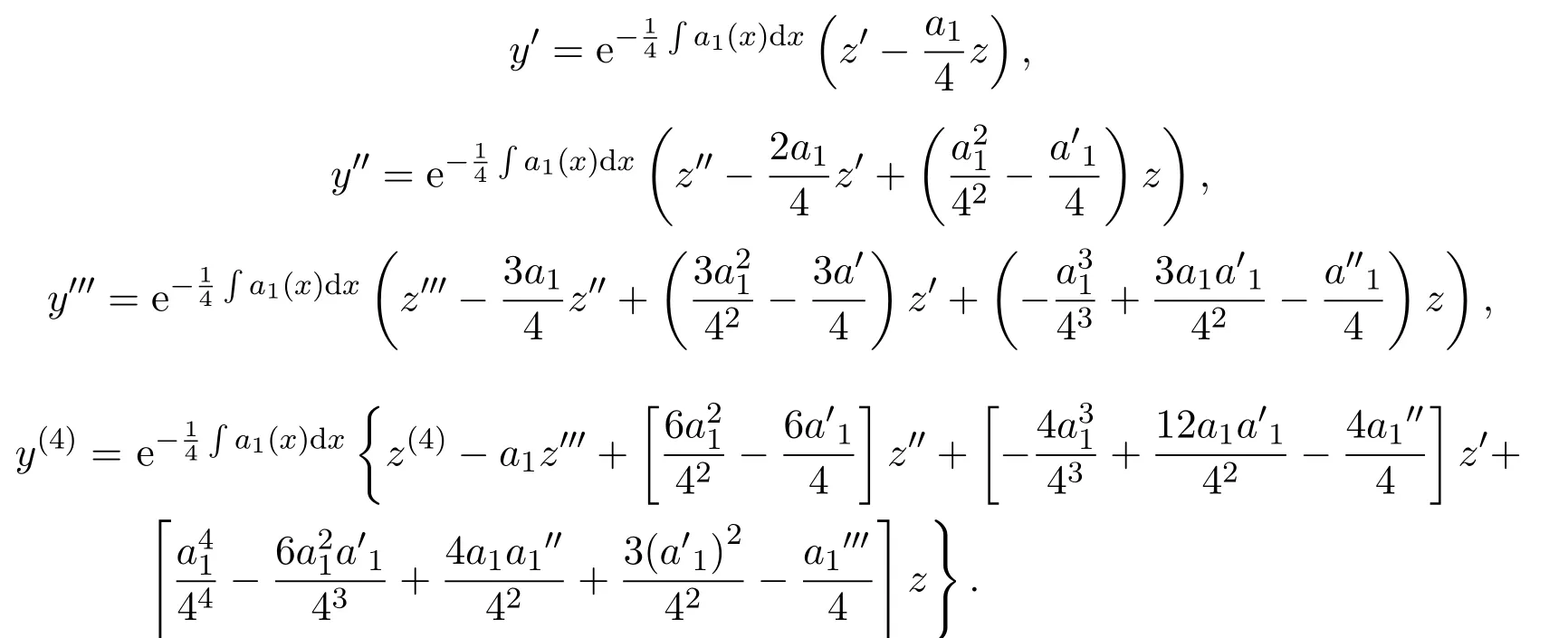
将y,y′,y′,y′′,y(4)及(4)式代入(3)式得到易求解四阶常系数线性非齐次微分方程:
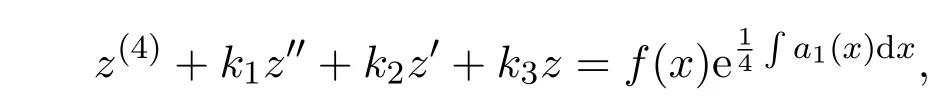
求出通解回代原来变量可得原方程通解.
定理3三阶变系数线性非齐次微分方程:
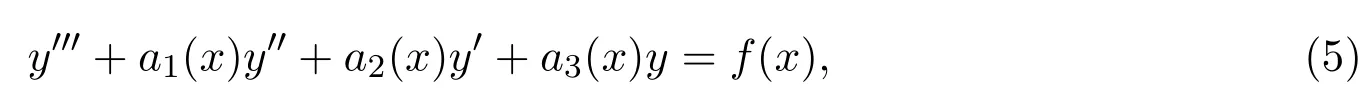
当系数满足:
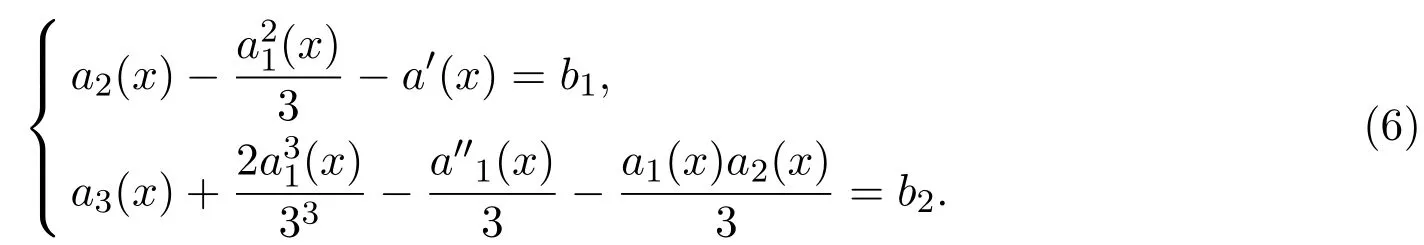
其中,bi(i=1,2)为常数.可通过变换
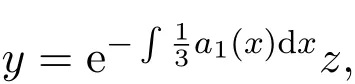
将(5)式化为三阶常系数线性非齐次微分方程求解.
证明令
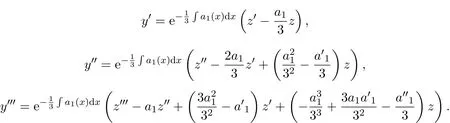
将y,y′,y′,y′′及(6)式代入(5)式可得易求解的三阶常系数线性非齐次微分方程:

求出通解回代原来变量可得原方程通解.
定理4[3]二阶变系数线性非齐次微分方程
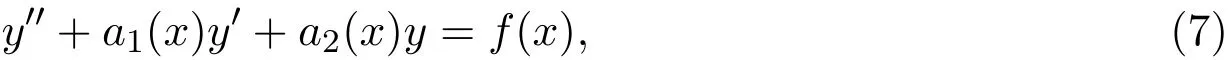
当系数满足:

3 主要结论的应用
例1[7]求解方程xy′+2y′−xy=ex.
解x/=0原方程改写为:

因为
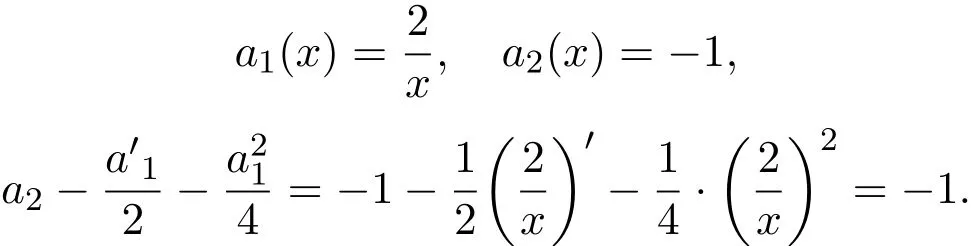
所以,(9)式可通过变换:
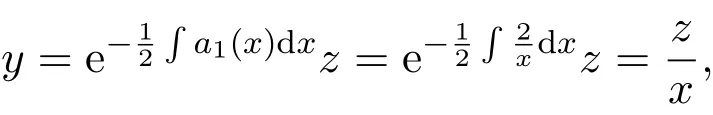
化为二阶常系数线性非齐次微分方程:

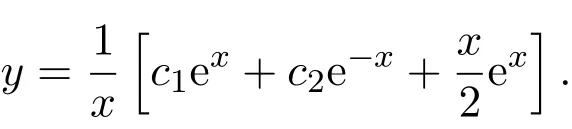
例2[8]求解方程x2y(4)+8xy′′+12y′+x2y=2ex.
解x/=0原方程改写为:
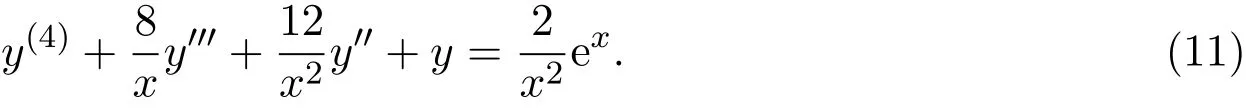
因为
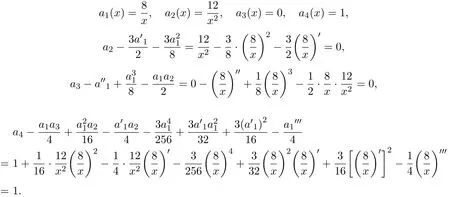
所以,(11)式可通过变换

化为四阶常系数线性非齐次微分方程:

用比较系数法求得(12)式通解:
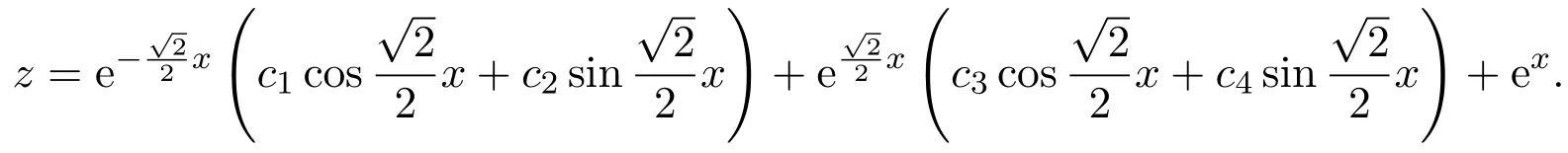
代回原来变量y,得到原方程的通解:
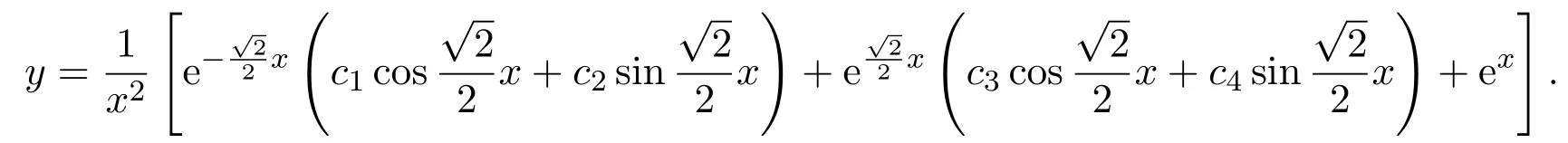
4 结束语
类似地,可以给出六阶变系数线性非齐次微分方程常系数化的条件.顺便指出,用这种方法可以得到更高阶变系数线性非齐次微分方程常系数化的条件,只是计算比较复杂.
[1]彭仕章.一类可积二阶变系数线性非齐次常微分方程[J].纯粹数学与应用数学,1993,9(2):99-100.
[2]冯伟杰,魏光美.二阶变系数线性微分方程的通解[J].高等数学研究,2012,15(3):28-30.
[3]敏志奇.一类变系数线性微分方程的可积定理及应用[J].甘肃高师学报,2010,15(2):6-7.
[4]贾庆菊.高阶变系数线性微分方程的解[J].中央民族大学学报学报:自然科学版,2012,21(2):32-35.
[5]贾庆菊,冯文俊,武跃祥.某些黎卡蒂(Riccati)方程的解[J].中央民族大学学报学报:自然科学版,2013, 22(1):48-51.
[6]王高雄,周之铭,朱思铭.常微分方程[M].3版.北京:高等教育出版社,2006.
[7]钟益林,彭乐群,刘炳文.常微分方程及其Maple,Matlab求解[M].北京:清华大学出版社,2007.
[8]庄万.常微分方程习题解[M].2版.山东:山东科学技术出版社,2004.
A solution of higher-order variable coefficient nonhomogeneous linear di ff erential equation
Jia Qingju
(Faculty of Applied Mathematics of Shanxi University Finance and Economics,Taiyuan030006,China)
The paper,by using higher-order relationship between of variable coefficient,through appropriate linear transformations of variables,and won fi ve-order variable coefficients linear di ff erential equation with constant sufficient conditions,gives a new solution to the higher-order variable coefficients linear non-homogeneous di ff erential equations.
higher-order,variable coefficients linear non-homogeneous di ff erential equation, linear transformation,constants coefficients linear non-homogeneous di ff erential equation, sufficient condition
O175
A
1008-5513(2014)03-0234-06
10.3969/j.issn.1008-5513.2014.03.003
2014-04-15.
国家自然科学基金(11126027);山西财经大学校级教改项目(2013132);山西财经大学校级教学团体项目.
贾庆菊(1956-),副教授,研究方向:常微分方程与应用数学.
2010 MSC:34B15

