一种求解非线性互补问题的filter内点算法
龙君,曾三云
(1.吉首大学民族预科教育学院,湖南吉首416000;2.吉首大学数学与统计学院,湖南吉首416000)
一种求解非线性互补问题的filter内点算法
龙君1,曾三云2
(1.吉首大学民族预科教育学院,湖南吉首416000;2.吉首大学数学与统计学院,湖南吉首416000)
利用Armijio条件和信赖域方法,构造新的价值函数.首次将内点算法与filter技术结合起来,提出一种求解非线性互补问题的新算法,即filter内点算法.在主算法中使用Armijio型线搜索求取步长,在修复算法中使用信赖域方法进行适当控制以保证算法的收敛性.文章还讨论了算法的全局收敛性.最后用数值实验表明了该方法是有效的.
非线性互补问题;filter方法;信赖域方法;Armijio条件;全局收敛性
1 引言
内点法[1-2]是一种比较成熟的最优化方法,有运用内点法求解非线性互补问题[3]的文献,比如文献[4-6]分别研究了某种特殊形式的非线性互补问题的内点算法.文献[7]提出了filter方法,有不少学者尝试将此方法与非线性互补问题结合起来处理[8-11].本文拟在文献[12]的基础上,利用Armijio条件和信赖域方法,构造一个新的价值函数,再结合filter技术,提出一种求解非线性互补问题的新算法,即filter内点算法.
在本文中,考虑的非线性互补问题(NCP)形式如下:

其中x∈Rn,f:Rn→Rn为一给定的函数,T为转置符号.易知NCP等价于非光滑方程组: H(x)=min{x,f(x)}=0.很显然,其零解正好是非线性互补问题(NCP)的解.

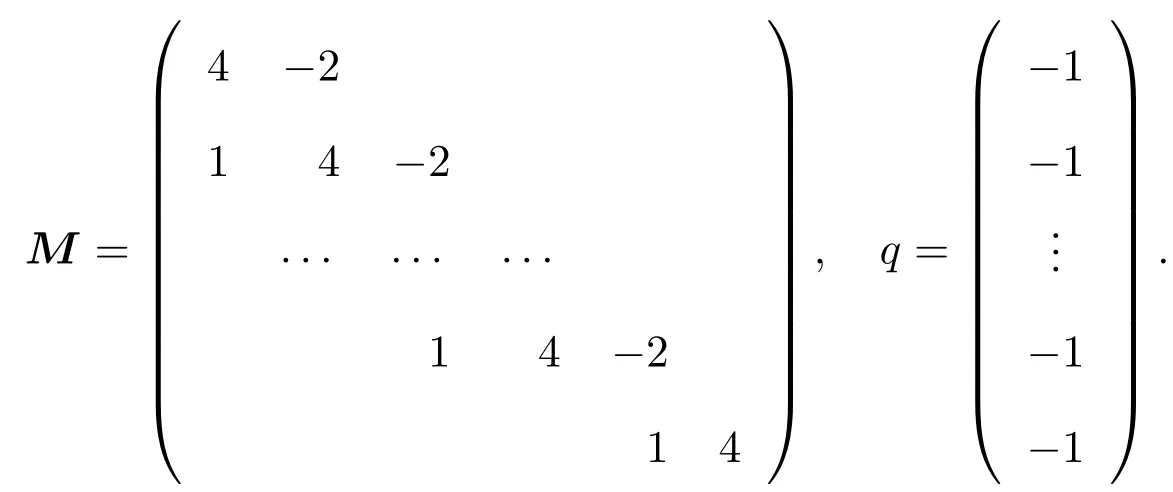
其中,Ix(x)={i:fi(x)>xi},Ie(x)={i:fi(x)=xi},If(x)={i:fi(x) 再令Jf(x)=Ix(x)∪Ie(x),定义一个n×n的矩阵A(x),设其第i列为: 其中ei是第i个位置为1其他全为0的列向量.若则∀d∈Rn,(2)式可变为: 2.1 基本性质 命题1[12]令是任意的,则对任意的序列和任意的序列有 定义如下价值函数: 其中 由命题1和(4)式,立即可得: 命题2[12]令∀x∗∈Ω是任意的.则对任意的序列和使{[(xk)−1]Tdk}有界的dk,有 在后面的算法中,c是可变的罚参数,而ζ是固定的数.由(4)式,有 则∀d∈Rn,Φc的方向导数为: 不等式(5)有两个重要的性质,归纳如下: 命题3[12]对固定的c>0,以下命题成立: 2)对任意的c>0,t∈R,∃a>0,使得 令 其中 由(3)式,(6)-(8)式,有 考虑以下线性系统: 其中M(x)=A(x)A(x)T+X−2是对称正定矩阵,且是(10)式的唯一解,则有d∗=−M(xk)−1wc(xk). 对(10)式先移项,然后两边同时左乘(d∗)T,并由(7)式及M(x)是对称正定矩阵,可得 于是,有Zc(x;d∗)<0⇔wc(x)/=0. 由此可得,若wc(x)/=0,则d∗是Φc(x)在x处的下降方向. 2.2 filter技术 对于某种最优化方法,希望发现一个满意的点,它不仅与目标函数相关,而且与约束条件也有联系.因此,先定义与NCP问题(1)的目标函数和约束条件相关的两个函数: 其中[f(x)]−=max{0,−f(x)},σ是一个常数.而且,x≥0总是得到满足. 定义1[8]一个点对(h(xk),p(xk))占优另一个点对(h(xi),p(xi))当且仅当h(xk)≤h(xi)且记作 由此概念,可以定义一个filter集合,在本文所给的算法中,它将被用作接收或拒绝一个试探点的准则. 定义2[8]filter集合是(指)这样(一个)序列点对(h(xk),p(xk))所组成的集合,使得彼此之间不相互占优.如果点对(hxk,pxk)不被filter集中的其他点对所占优,则说它是可以接受的. filter方法就是将这些“好点”放进filter集,记为F.在第k个点处,如果一个新点能被filter集合接收,则更新 为方便起见,记Dk+1={i|hi≥hk,pi≥pk,(i∈)},其中hi=h(xi),pi=p(xi),则 为得到收敛结果,给出如下的filter准则: 其中,第一个不等式表示h下降,而第二个不等式可得到p的一个充分下降.这个准则可以保证下一节中的主算法1所产生的迭代点趋向可行点. 本文结合Armijio条件、信赖域方法和filter技术,提出求解NCP问题的一个新算法,具体步骤如下: 算法1(filter内点算法) 步3若||wk||≤δ,则令转步2; 令mk为最小的非负整数m,使得 步8若θ(xk)=0,停止.否则令k:=k+1,转步2. 需要注意的是,当mk≥1时,因为mk满足(12)式,所以mk−1一定不满足(12)式,于是有 算法2(修复算法) 步2计算 步3计算 如同文献{[14-}17],对于算法1的收敛性分析基于以下假设: H1:集合xk∈X非空有界; H2:函数F(x)在包含于X的开集上二次连续可微; H3:在求解(14)时,有 其中β2>0为一正常数; 引理1每一个新的迭代点都被filter集合F接受. 证明由算法1知,新迭代点在步7产生.故新的迭代点xk+1被filter集合接收.于是引理得证. 下面分析由算法1所产生的序列{xk}的收敛性. 定义3[12]向量x≥0被称为是S-正则的,如果对变量d∈Rn,以下线性不等式有解 引理2[12]假定罚参数序列c可以无限次更新,x∗是子序列{xk:k∈K}的聚点,则序列{uk:k∈K}有一个聚点u∗,并满足: 其中 引理3[12]令是给定的,对任意的d∈Rn,定义: 令θx:为齐一次的函数且满足: 考虑以下条件: (a)x是一个S-正则向量; 即 则有以下结论:(a)⇒(b)⇒(c)⇔(d). 定理1假设x∗是序列{xk:k∈K}的一个聚点. 1)若算法1中的罚参数序列{ck}被有限次更新,则 2)若算法1中的罚参数序列{ck}可以无限次更新,并且x∗是S-正则的,则θ(x∗)=0. 证明1)因为{ck}被有限次更新,由算法1的步3和步5知,存在指标k0和常数c>0,使得对任意的k≥k0,有||wk||>δ,ck=c. 现假设(15)不成立,即存在常数ε>0和子序列{xk:k∈K},使得 其中K⊂{k0,k0+1,………}.由(9)式中的Φ′(xk;dk)≤Z(xk;dk)和(11)式中的Zc(xk,dk)≤0,可知{Φc(xk):k∈K}是单调递减的,而且,(16)式暗示着{Φc(xk):k∈K}下有界.因此,序列收敛.再由(12)和(13)式,有 由命题3中的(2)和(16)式,有 即{xk:k∈K}有界,且对任意的k∈K,有 由此易知,∀k∈K,∃T>0,使得 当||wk||≥δ时,由(7),(10)和(11)式可得,对任意的k∈K,有 再由(17)和(19)式,有 根据τk的定义,对任意的k∈K,若否则,由(18)式及的某些分量趋于0的事实易知,因此 再注意到(20)式,它意味着 记λk=||dk||.由(20)式,有不难证明{[(xk)−1]Tdk}有界.因此由命题2,有 这与(21)式相矛盾!于是(15)式成立. 2)现假设θ(x∗)/=0.由引理2知,uk:k∈K→u∗,不难得知函数θx(d)=dTu∗满足引理3.又因为x∗是S-正则的,且θ(x∗)>0,由引理3中的(d)知,存在向量使得dTu∗<0,这与引理2相矛盾!于是有θ(x∗)=0. 给出算法的一些数值结果:终止条件为:ε=10−13. 例1考虑如下测试函数: 选取不同初始点的数值,结果由表1给出. 表1问题1的数值结果 其中,“迭代次数”栏中,括号中的数据表示文献[12]中的结果.由此可以看出,当初始点的选取离解较远时,结果还是比较好的. 例2考虑如下测试函数:f(x)=Mx+q,其中矩阵M和向量q分别具有如下形式: 此问题的解为:x∗=(1,0,………,0)T.选取的初始点为x0=(1,1,………,1)T,其数值结果由表2给出 表2问题2的数值结果 其中“迭代次数”栏中,括号中的数据表示文献[12]中的结果.由此可以看出,当维数比较高时,的结果还是比较理想的. 文献[12]给出了求解NCP问题的正内点算法,而文献[9-11]提出了用filter方法来求解NCP问题.本文结合他们的优点,提出了一个新的算法,即filter内战算法.在主算法中使用Armijio型线搜索求取步长,在修复算法中使用信赖域方法进行适当控制以保证算法的收敛性. [1]龚小玉,张明望.求解P∗(K)-阵线性互补问题的高阶仿射尺度内点算法[J].纯粹数学与应用数学,2008, 24(4):699-705. [2]孙清滢,常兆光,王清河.一个求解线性不等式约束的非线性规划的广义梯度投影内点算法[J].纯粹数学与应用数学,1999,15(1):92-98. [3]雷飞燕.无穷维Hilbert空间中的伪单调非线性互补问题[J].纯粹数学与应用数学,2010,26(3):417-419. [4]王浚岭.基于代数等价路径的一致P-函数非线性互补问题的可行内点算法[J].应用数学,2007,20(2):351-356. [5]朱德通,蔡力.线性不等式约束的广义非线性互补问题的仿射内点信赖域方法[J].数学年刊:A辑,2010, 31(1):13-34. [6]陈华平,张明望.单调非线性互补问题基于一类核函数的原始-对偶大步校正内点算法[J].中国科学技术大学学报,2011,41(9):796-803. [7]Fletcher R,Ley ff er S.Nonlinear programming without a penalty function[J].Mathematical Programming, 2002(91):239-269. [8]聂普炎.优化中的筛选法[D].北京:中国科学院计算数学与科学工程计算研究所博士学位论文,2002. [9]Nie P.A filter method for solving nonlinear complementarity problems[J].Applied Mathematics and Computation,2005,167(1):677-694. [10]Long J,Zeng S.A projection-filter method for solving nonlinear complementarity problems[J].Applied Mathematics and Computation,2010,216(1):300-307. [11]Long J,Zeng S.A new Filter-Levenberg-Marquardt method with disturbance for solving nonlinear complementarity problems[J].Applied Mathematics and Computation,2010,216(2):677-688. [12]Ma C,Liang G,Chen X.A positive interior-point algorithm for nonlinear complementarity problems[J]. Applied Mathematics and Mechanics,2003,24(3):355-362. [13]Pang J S.Newton′s method for B-di ff erentiable equations[J].Journal of Mathematics in Operational Research,1990,15(2):311-341. [14]Audet C,Dennis J E.Combining pattern search and algorithms for derivative free optimization[J].SIAM Journal on Optimization.2004(14):980-1010. [15]Fletcher R,Ley ff er S.A Boundle Filter Method for Nonsmooth Nonlinear Optimization[R].Dundee:Department of Mathematics,Scotland,University of Dundee,1999. [16]Fletcher R,Leyfer S,Toint P L.On the Global Convergence of an SLP-Filter Algorithm[R].Dundee: Department of Mathematics,University of Dundee,1998. [17]Powell M J D.Convergence Properties of a Class of Minimization Algorithms[C]//Mangasarian O L,Meyer R R,Robinson S M.Nonlinear Programming.New York:Academic Press,1975. A filter interior-point algorithm for nonlinear complementarity problem Long Jun1,Zeng Sanyun2 A new merit function is constructed by using Armijio conditions and the trust region method.Then fi rstly combining the interior-point method with filter technique,we propose a new algorithm to solve nonlinear complementarity problem.In the main arithmetic,step length is produced by Armijio type line search,and in the repair algorithm,trust region method is used to properly control so as to ensure the convergence of the algorithm.We also discuss the global convergence of the algorithm.Finally,the numerical experiments show that the method is e ff ective. nonlinear complementarity problem,filter method,trust region method,Armijio conditions, global convergence O224 A 1008-5513(2014)03-0245-10 10.3969/j.issn.1008-5513.2014.03.005 2013-11-28. 湖南省教育厅科学研究项目(10C1126,10B088). 龙君(1973-),博士生,讲师,研究方向:最优化理论与方法. 2010 MSC:09C30

2 预备知识
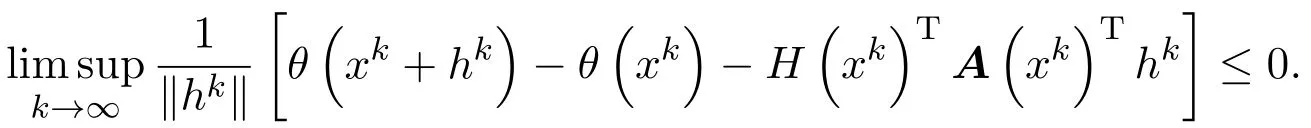

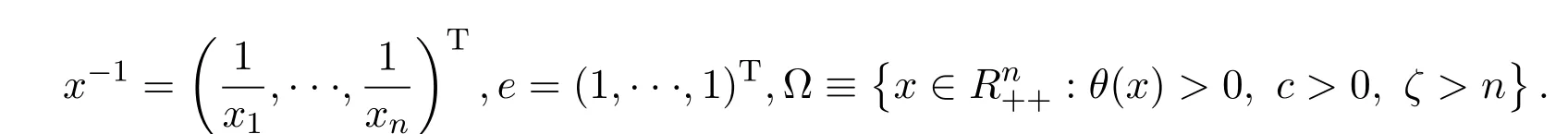










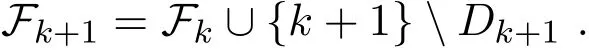


3 filter内点算法

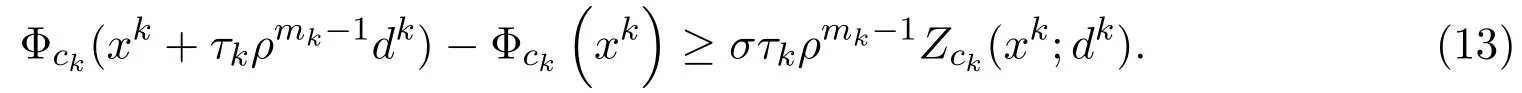
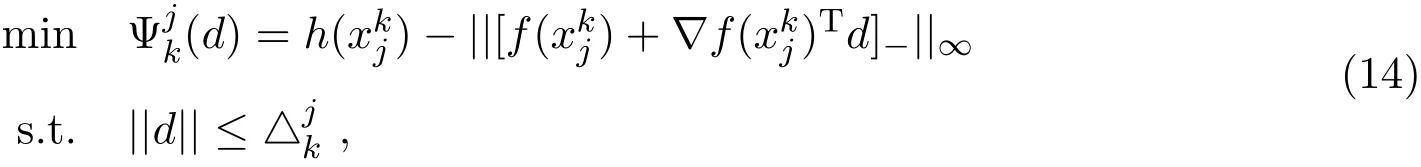

4 收敛性分析
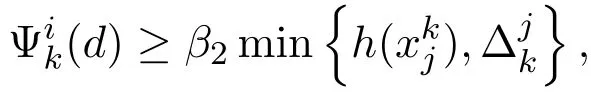


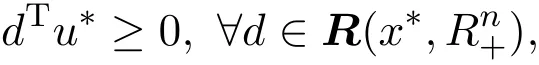














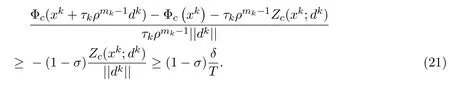

5 数值实验



6 结论
(1.School of Preparatory Education for Minority Nationalities,Jishou University,Jishou416000,China; 2.College of Mathematics and Statistics,Jishou University,Jishou416000,China)

