关于Camassa-Holm方程动量密度的紧支集在半轴上的估计
康顺光,贾佳
(塔里木大学信息工程学院,新疆阿拉尔843300)
关于Camassa-Holm方程动量密度的紧支集在半轴上的估计
康顺光,贾佳
(塔里木大学信息工程学院,新疆阿拉尔843300)
主要考虑在半轴上Camassa-Holm方程解的动量密度紧支集大小的估计,方法是根据区间长度与区间特征值的关系,通过估计第一Dirichlet特征值来估计动量密度紧支集的长度.因为知道动量密度紧支集外解的性态,所以通过估计动量密度支集的大小可以得到方程解的更多信息.
Camassa-Holm方程;动量密度;紧支集;半轴;特征值
1 引言
本文主要是考虑半轴上Camassa-Holm方程解的动量密度紧支集的估计.首先,给出半轴上的Camassa-Holm方程:
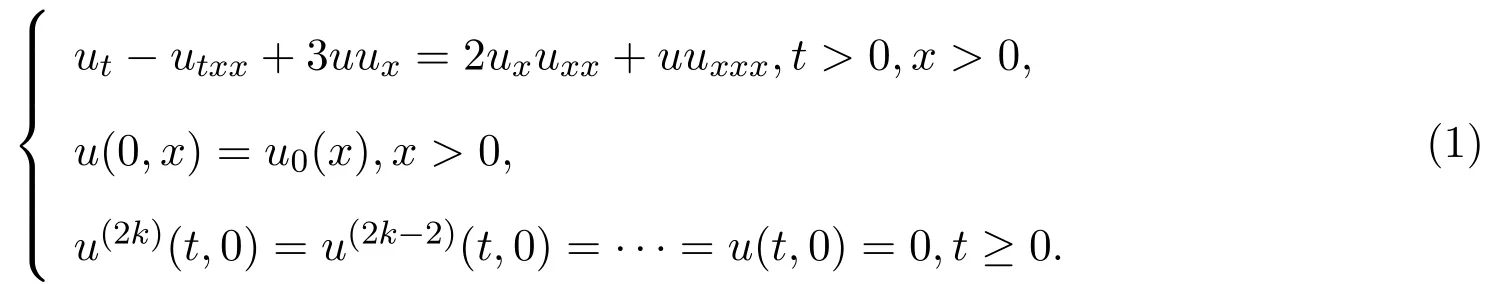
令m(t,x)=u(t,x)−uxx(t,x)为动量密度,则u满足方程(1)蕴含m满足:
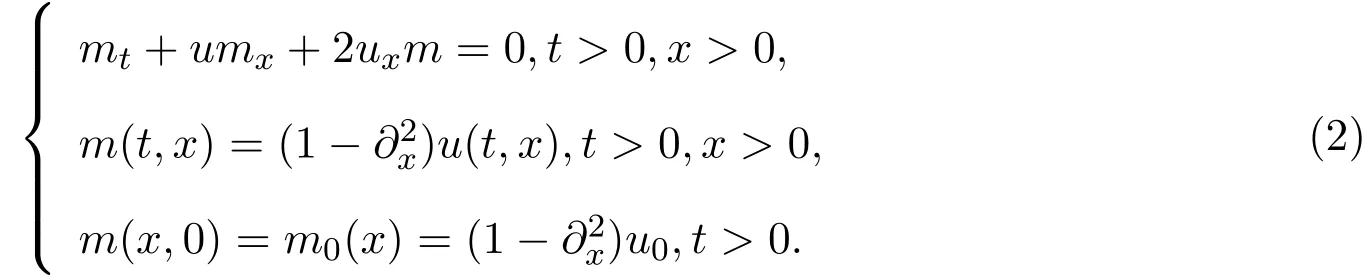
浅水波方程可以由不可压流体的维欧方程在无旋、浅水、小波幅的假定下,在二维自由表面区域的引力作用下用逼近的方法得到.例如著名的KdV方程、Camassa-Holm(CH)方程和Degasperis-Procesi(DP)等[14].本文主要是受二维欧拉流的涡量片大小的估计研究所启发,来研究一维的Camassa-Holm方程.CH和DP方程的动量密度与欧拉流的涡量很相似,它们都满足一阶非线性非局部的偏微分方程,并且支集都随着流线流.但二者也有差别,二维涡量沿流线流时值不变,动量密度不是;欧拉方程描述不可压缩流体,即欧拉流是保持体积的,但CH方程只是欧拉方程的逼近,CH流不再是保持体积的.文献[5]通过估计特征值来估计二维涡片支集的内半径和周界,下面就是利用类似于文献[5]中的方法来估计m的支集的大小,以便更加清楚地了解解u不清楚地方的大小.
2 主要结论
本文主要是估计在半轴上CH方程解的动量密度紧支集的长度.对于动量密度m的紧支集的长度,容易得到一个线性的上界估计,而本文是给出其一个下界估计.不失普遍性,可设初始动量密度的支集是有限区间.若它不连通,可对它的连通分支或凸包作同样的讨论,得到它的性质.
设微分方程:
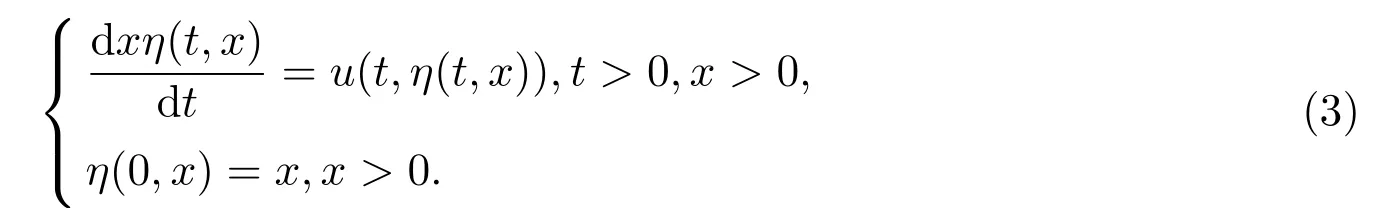
若方程(2)的初值m0有紧区间[c,d]为支集,那么m(t,…)也有紧支集[η(t,c),η(t,d)],即(t,η(t,x))表示从x出发的流线.设D(t)=[η(t,c),η(t,d)],知道方程(1)的解u在区域D(t)之外具体的形式是指数函数,并且在正轴远方永远为正,在负轴远方是负[6];但是方程(1)的解u在区域D(t)之内的情况不太清楚,本文的任务就是估计动量密度m(t,x)的紧支集D(t)在半轴上的大小.

在u0∈G4(+)下考虑,此时存在一个极大时间T∗=T∗(u0)>0,当T∈(0,T∗)时,方程(1)在[0,T]上有唯一解[7]:
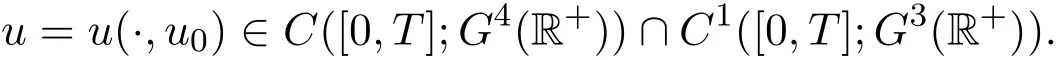
此时,
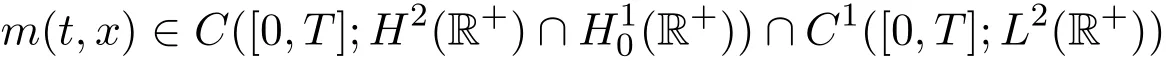
是方程(2)的解.
定理2.1假设
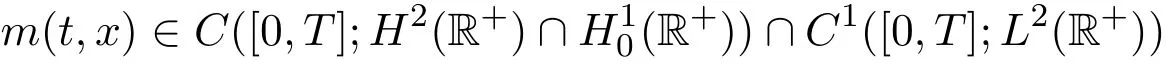
是方程(2)的强解,

连通,如果当[0,T]×R+时,|ux(t,x)|≤M.则
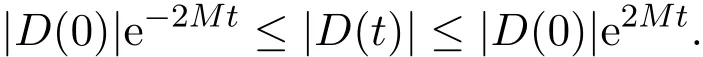
其中,
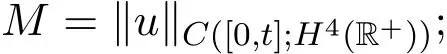
若u的动量密度m不变号,M可取为
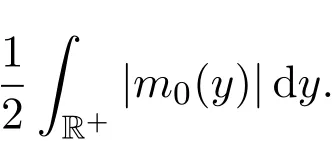
3 主要定理证明
为了主要定理2.1的证明,首先给出下面几个结论.
性质3.1如果u是方程(1)的解,m为u的动量密度,那么
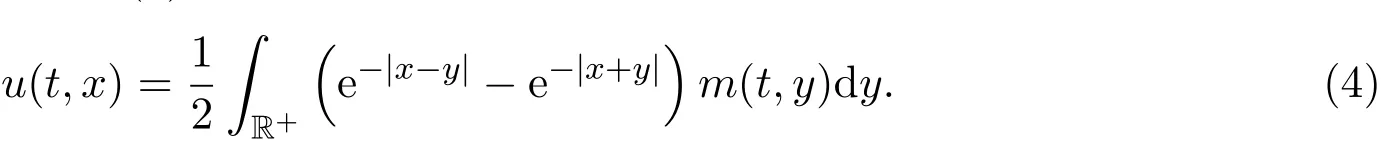
证明记
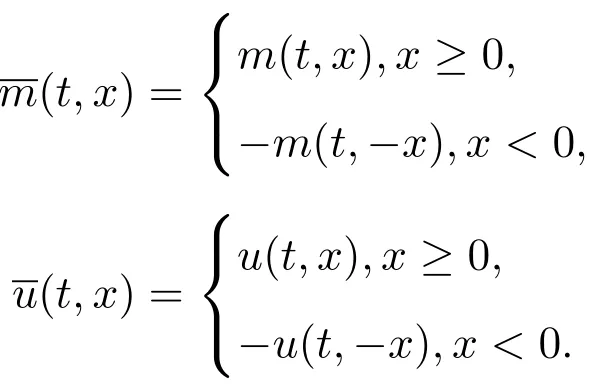
为了方便,以下证明略去t.当x<0时,
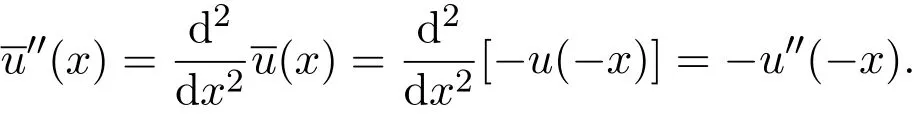
则
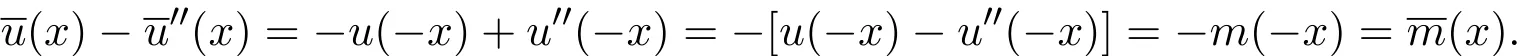
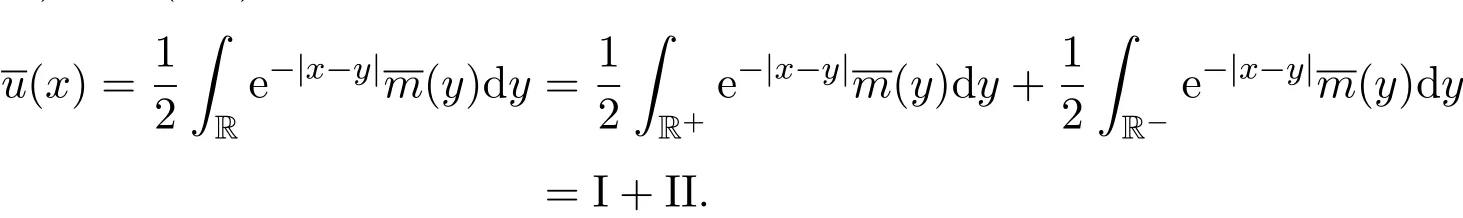
因为
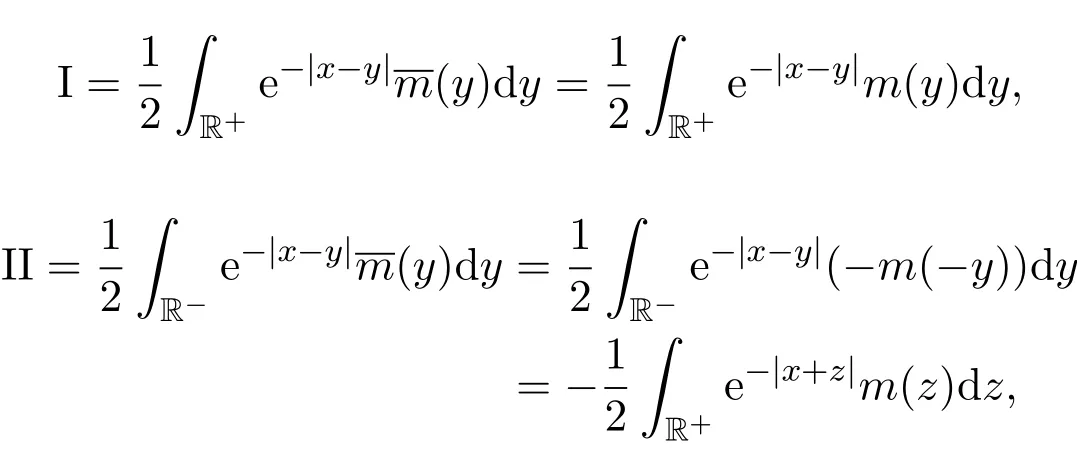
所以
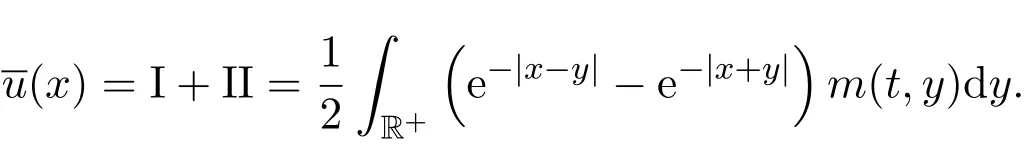
于是命题得证.
性质3.2假设存在一个极大时间T∗=T∗(u0)>0,对于T∈(0,T∗),
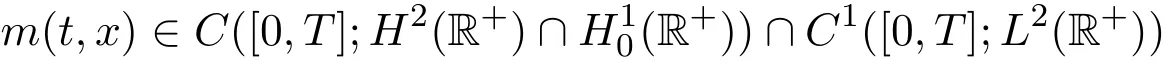
是方程(2)的解,则

证明由性质3.1易知,
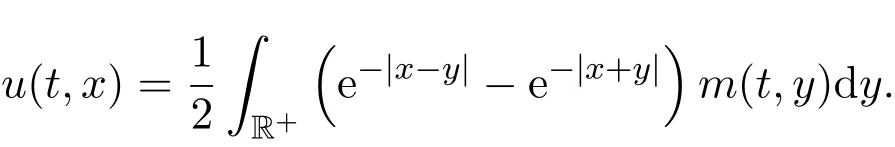
对上面u(t,x)关于x求偏导数,得
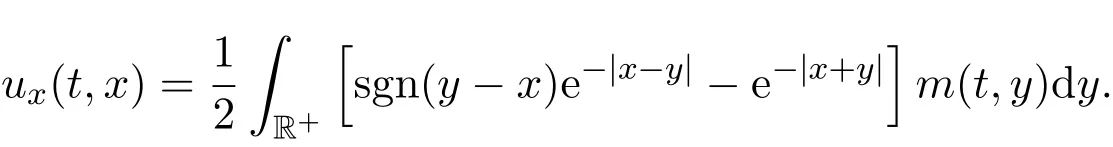
然后,对ux估计,得
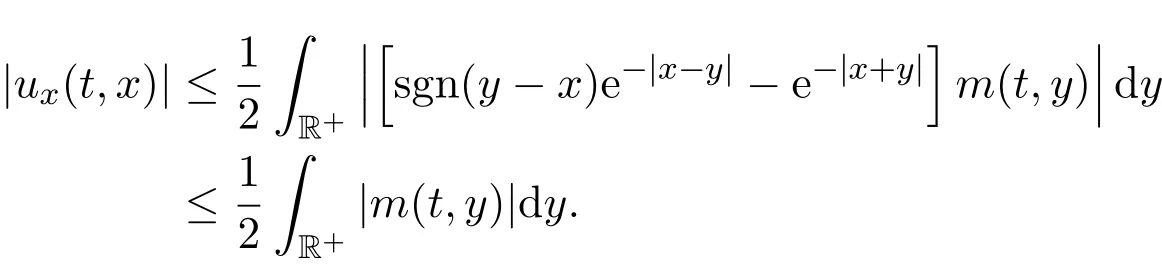
命题得证.
性质3.3设
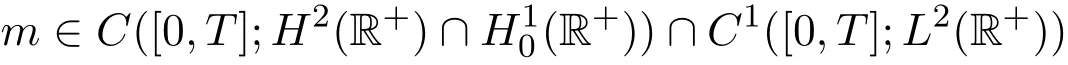
是方程(2)的解,则
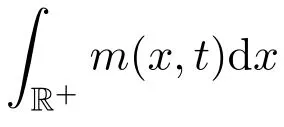
是t的减函数.
证明易知mt+umx+2uxm=0,则
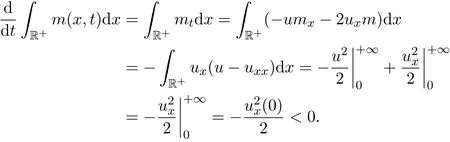
命题得证.
性质3.4设
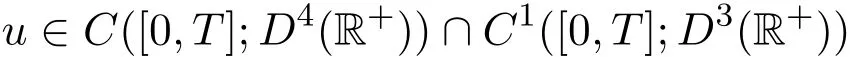
是方程(1)的强解,且T∗=T∗(u0)>0是u存在的极大时间.若T∈(0,T∗),令


证明从u∈C([0,T];D4(+))得
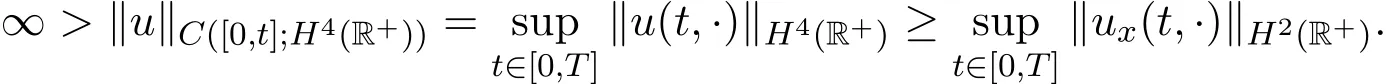
由Sobolev嵌入定理知,H2(+)L∞+)∩C(+),所以
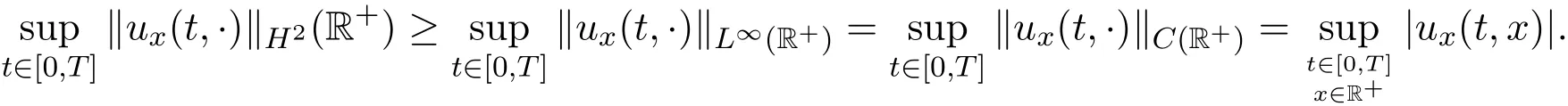
注3.1若u的动量密度m不变号,则由性质3.2和性质3.3可知
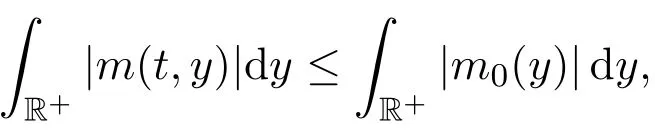
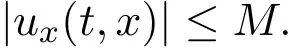
性质3.5(Rayleigh公式)设Ω⊂是开区间,λ1(Ω)为−△在Ω上的第一个Dirichlet特征值,则
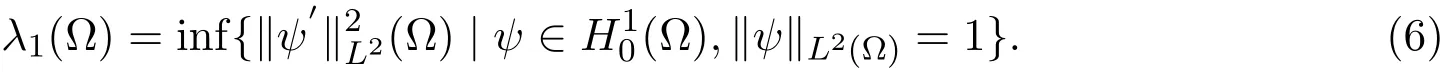
定义3.1设u是方程(1)的解,对于s,s+t∈(0,T),定义η(t;α,s)是以下问题的解:
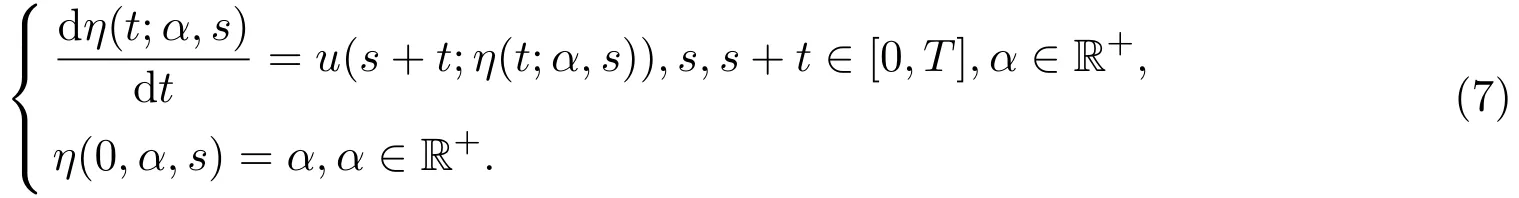
当t=0时,流的速度是u(α,s),且η(t;…,s):R+→R+是微分同胚.
定义3.2设ψ∈L2(D(s)),s∈(0,T),对于s+t∈(0,T),定义ψt∈L2(D(s+t))为

其中η(t;α,s)满足(7)式.
引理3.1假设定理2.1的条件成立,α∈D(s),对于s,s+t∈(0,T)有:
(a)如果η(t;α,s)是定义3.1中所述,那么

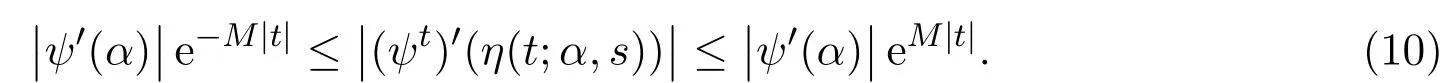
(c)如果ψ∈L2(D(s)),那么
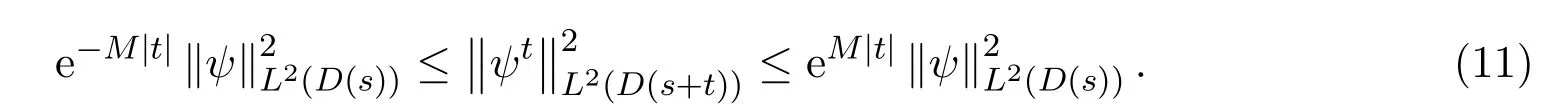
引理3.2假设定理2.1的条件成立,那么,对于s,s+T∈(0,T)有
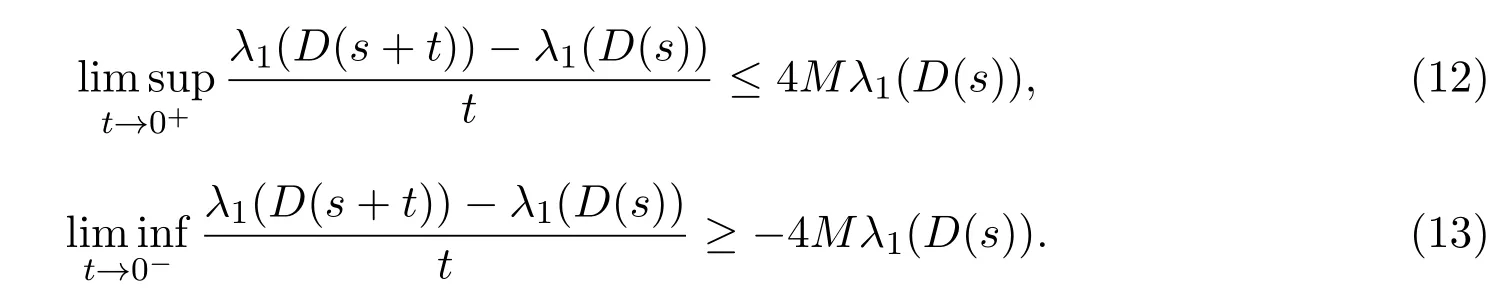
引理3.3假设定理2.1的条件成立,那么,对于s,s+T∈(0,T)有

以上三个引理在文献[8]中被证明,此处不再证明.
定理2.1的证明综合引理3.2和引理3.3可知λ1(D(s))Lipsschitz连续存在,并且有,
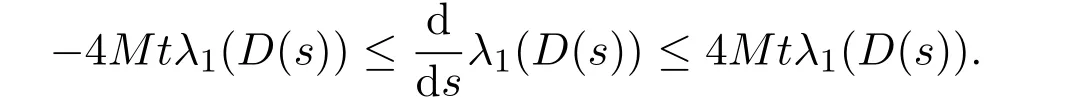
最后,对上式运用Gronwall不等式,得到
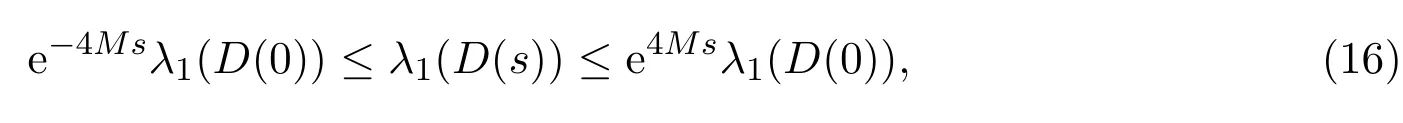
其中λ1(s)=π2/|D2(s)|,所以
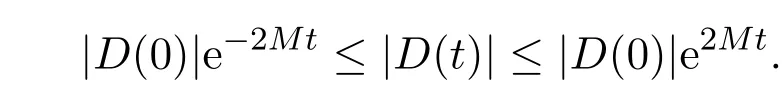
参考文献
[1]Korteweg D J,Vries G D.On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves[J].Philos.Mag.,1895,39:422-443.
[2]Camassa R,Holm D D.An integrable shallow water equation with peaked solitons[J].Phys.Rev.Lett., 1993,71:1661-1664.
[3]Degasperis A,Procesi M.Asymptotic Integrability:Symmertry and Peturbation Theoty[M].Singapore: World Scienti fi c,1999.
[4]Degasperis A,Holm D D,Hone A N W.Anew Integrable equation with peakon soiotons[J].Theo.Math. Phys.,2002,133:1463-1474.
[5]Namkwon Kim.Eigenvalues associated with the vortex patch in 2-D Euler equations[J].Math.Ann., 2004,330:747-758.
[6]Himonas A,Misiolek G,Ponce G,Zhou Y.Persistence properties and unique continuation of solutions of the Camassa-Holm equation[J].Comm.Math.Phys.,2007,271:511-522.
[7]Escher J,Yin Z.Initial boundary value problems of the Camassa-Holm equation[J].Communications in Partial Di ff erential Equations,2008,33:377-395.
[8]Kang Shunguang,Tang Taiman.The support of the momentum density of the Camassa-Holm equation[J]. Applied Mathematics Letters,2011,24:2128-2132.
The estimate of the compact support of the momentum density of the Camassa-Holm equation on the half-line
Kang Shunguang,Jia Jia
(College of Information Engineering,Tarim university,Alar843300,China)
The paper consider the bounds for the size of the support of a compactly supported momentum density of the Camassa-Holm equation on the half-line.This is achieved by estimating the fi rst Dirichlet eigenvalue of the support,according to the relations between the eigenvalues and the geometric properties of a domain.Because the behavior of the solution outside the support of the momentum density is known.By estimating the size of the momentum density to obtain more information on the solution.
Camassa-Holm equation,momentum density,compact support,half-line,eigenvalue
O175
A
1008-5513(2014)03-0264-07
10.3969/j.issn.1008-5513.2014.03.007
2014-02-14.
康顺光(1983-),硕士,讲师,研究方向:偏微分方程.
2010 MSC:35G25
——对2018年广州市一道中考题的研究

