基于ModelCenter的精密气浮工件台系统建模与参数优化*

陈鹏飞,王彦伟

(华中科技大学 国家CAD支撑软件工程技术研究中心， 武汉 430074)

基于ModelCenter的精密气浮工件台系统建模与参数优化*

陈鹏飞,王彦伟

(华中科技大学 国家CAD支撑软件工程技术研究中心， 武汉 430074)

针对精密气浮工件台运动时部件会不可避免地产生偏转和振动，建立了精密气浮工件台的系统模型，包括工件台几何模型, 直线电机模型，气体轴承模型。在设定工况下对工件台系统的动态特性进行了数值仿真分析，得到了工件台系统的运动偏转误差曲线和气膜的垂向振动曲线,为工件台系统的设计提供了重要的理论参考价值。基于多学科协同设计集成优化平台ModelCenter进行系统集成，并建立了精密气浮工件台的多学科设计优化模型。利用遗传算法实现了精密气浮工件台的总体参数优化设计，优化结果满足设计要求。

ModelCenter;精密气浮工件台;系统模型;参数优化;偏转振动

0 引言

光刻机是半导体制造业的重要设备，高度集成了诸多现代科学技术。精密气浮定位工件台则是光刻机极其重要的关键部件，直接决定了光刻机的工作性能[1]。研究气浮定位工件台的动态特性对于提高光刻机的工作性能意义重大。精密气浮定位工件台主要分为粗动台和微动台两级平台。粗动台提供低精度的长行程运动，微动台则提供高精度的短行程运动，本文只针对粗动台的性能做出研究。气浮定位工件台多采用气体轴承进行承载和导向，直线电机直接驱动，结构上具有无机械接触的特点。按拓扑结构分，精密气浮定位工件台主要有H型、口子型以及L型等典型结构。不管是哪一种拓扑结构的工件台在运动时都会因为气体轴承的气膜振动以及电机输出力不同步等因素使得运动部件产生偏转和振动[2-4]。因此精确计算出运动部件的偏转量和振动量这些动态性能，在设计阶段对工件台进行参数优化，有助于提高工件台的运动精度。

气浮定位工件台动态性能分析的一般方法是将气体轴承等效为弹簧，对原系统进行简化，建立工件台动力学模型。Chen X.等采用弹簧单元来模拟气体轴承刚度的波动，提出了精密气浮定位工件台关于静压气浮支承刚度的数值优化方法[5]；Cai Tian等将气体轴承等效为一系列线性和扭转弹簧来分析定位工件台的振动特性[6]；张从鹏等利用有限元计算方法对气浮支承的动态特性进行了详细设计分析，并将结果运用到气浮工件台的动态性能分析中[7]。以上几种方法将气体轴承等效为线性弹簧，在分析过程中，弹簧的刚度系数是不变的。而事实上气体轴承的刚度系数是在不断变化的，一旦工件台的运动精度要求提高，这些方法将不再满足设计的要求。

本文以一种H型工件台作为典型研究对象利用实验方式获得气体轴承的承载力曲线，消除了气体轴承的非线性影响，对气浮定位工件台进行参数化建模，研究气浮定位工件台的动态性能，并利用ModelCenter[8]多学科优化工具对工件台性能进行基于气体轴承分布位置的优化。

1 气浮定位工件台系统建模

典型的H型气浮定位工件台系统模型主要由几何模型，直线电机模型，气体轴承模型组成。

1.1 工件台几何模型

几何外形模型主要确定工件台系统的外形尺寸，并进行三维参数化建模。一个典型的H型气浮定位工件台结构示意图如图1所示。几何模型主要由滑块，横梁，导轨以及基座等元件组成。横梁两端分别与两个相互平行的直线电机Y1、Y2的动子连接，实现Y方向的双边同步驱动；X向直线电机的定子安装在横梁上，其动子与滑块固接，实现X方向的运动。横梁、滑块均通过气体轴承支承和导向。

图1 气浮工件台三维示意图

图2 气浮工件台俯视示意图

描述H型气浮运动平台的重要尺寸参数如图2所示。图中,红色矩形块表示导向气体轴承，而绿色圆形块则表示承载气体轴承。w1和w2分别表示安装在横梁同侧的一对导向气体轴承和一对承载气体轴承的间距；w3和w4分别表示安装在滑块相同一侧的导向气体轴承对和承载气体轴承对的间距；w5和w6则分别表示安装在滑块两侧的导向气体轴承对和承载气体轴承对的间距；s1和s2分别表示安装在横梁上的一对导向气体轴承和一对承载气体轴承之间的跨距；s3表示Y向两直线电机驱动力之间的跨距。表1给出了部分尺寸参数的初始值。

本文利用ModelCenter中所集成的Pro/E软件对工件台进行三维参数化建模，可以实现ModelCenter和Pro/E之间的实时通信，实现分布式计算，减轻了计算机的负荷。在ModelCenter中改变参数的结果可以实时相应地反映在Pro/E造型中。

表1 工件台重要尺寸参数列表及其初始值

1.2 直线电机模型

永磁同步直线电机[9-10](Permanent Magnetic Linear Synchronous Motors PMLSM)因其响应快、直接驱动的特点广泛应用于各种精密、超精密加工设备中。精密气浮工件台系统就采用PMLSM作为驱动工件台部分的执行机构。鉴于PMLSM的强耦合性和非线性，为了便于分析，将电机方程按照统一电机理论做线性变换，实现耦合方程的解耦。建立在轴坐标系下的PMLSM数学模型如下：

定子电压

(1)

定子磁链

(2)

电磁推力

(3)

电机机械运动方程

(4)

上述各式中：ud，uq，id，iq，ψd，ψq，Ld，Lq分别表示永磁同步直线电机d轴和q轴的电压，电流，磁链，电感，Rs表示PMLSM的定子电阻，ω为PMLSM直线速度折合成的等效旋转电机角速度，ω=πv/τ，v为动子的运动速度，τ为极距，P为电机的极对数，Fe为电磁推力，Fl为负载阻力，B为粘滞系数，m为电机运动部分的质量，包括动子以及动子所带动负载的质量。

基于上述理论，直线电机模型可有Matlab中的Simulink模块来实现。ModelCenter的外部组件功能可以完成与Matlab程序的连接，将Matlab中的计算结果返回到ModelCenter中。

1.3 气体轴承模型

气体轴承作为定位工件台导向和承载的关键部件，其性能的好坏直接影响到整个平台系统的动力学性能。气体轴承的工作原理如图3所示，气源提供的高压气体P0流经节流孔和真空腔进入气体轴承间隙，并扩散到大气中，从而在气体轴承承载面形成具有一定承载力和刚度的高压气膜[11]。

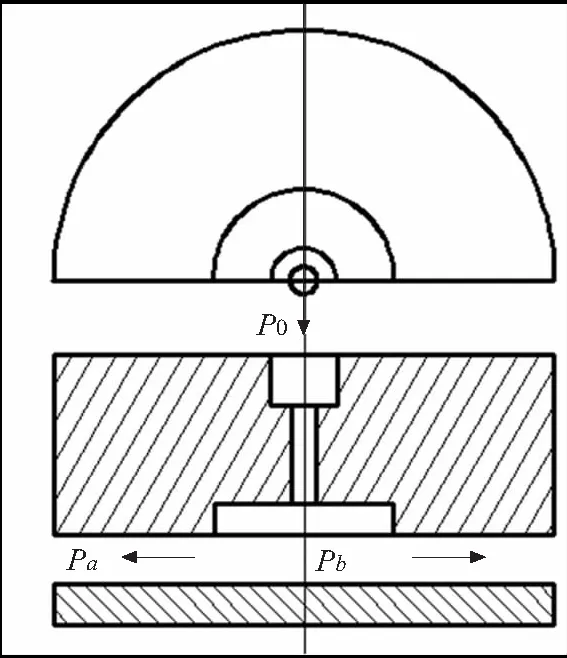
图3 气体轴承工作原理示意图

在供气压力一定的情况下，气体轴承的受力情况仅与所产生的高压气膜厚度有关。气体轴承的动力学建模就是要建立气浮承载力与气膜厚度的关系曲线。本文以一种典型的环形止推气浮支承作为应用实例，通过实验方式获得气体轴承在供气压力为定值的情况下承载力与气膜厚度的关系数据。利用Matlab软件将这些数据拟合，获得最终的承载力和气膜厚度关系曲线如图4所示，图中横轴表示气膜厚度，纵轴则为气浮承载力。表2则给出了相应气体轴承的关键结构尺寸。

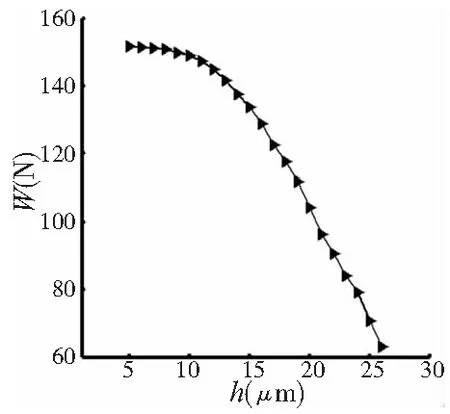
图4 供气压力为0.3MPa时的承载力曲线

由实验结果可知对于给定的气体轴承，如果供气压力保持不变，随着气膜厚度的变大，其承载力不断降低，当气膜厚度增加或减小到一定程度时，承载力随气膜厚度的变化趋势不再明显。同时需要指出的气浮支承的承载力与气膜厚度具有很强的非线性关系。通过实验所获得的数据在仿真过程中可以实时地获得气体轴承的实际刚度，更加接近气体轴承刚度的真实值，这样就降低了因线性化处理所带来的计算误差。

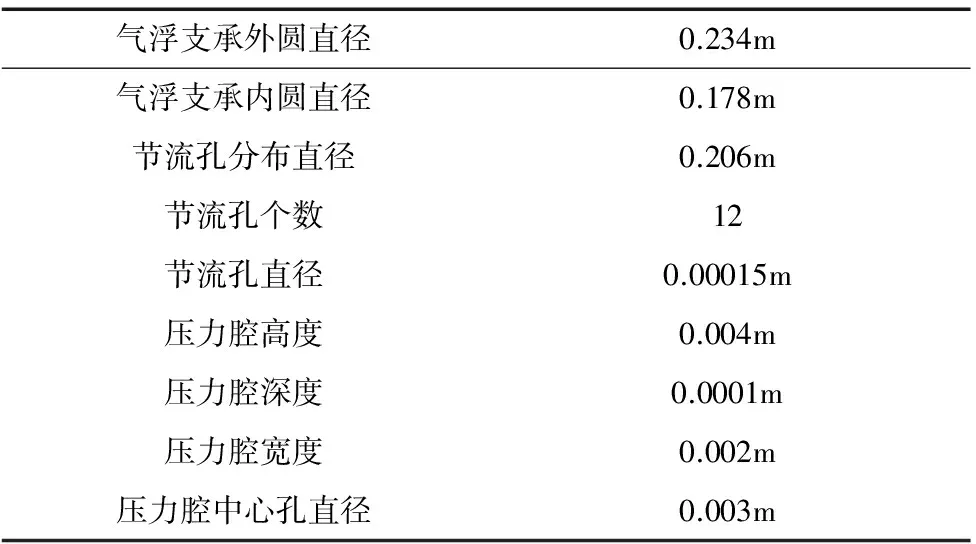
表2 气浮支承关键结构尺寸

2 仿真结果与分析

将上述已经建立的几何模型，直线电机模型以及气体轴承模型利用ModelCenter的QuickWrap技术封装起来，通过组件连接的方式建立工件台系统的ModelCenter仿真模型如图5所示。

图5 工件台系统仿真模型

在本仿真实验中气浮定位工件台的具体结构参数的初始值如下：横梁的质量为52.4kg，滑块的质量为8.2kg，转动惯量分别为J1=diag(0.601032,0.626628,0.426600)J2=diag(0.010798,0.020200,0.022308)单位均是kg·m2。其他结构参数的初始值见表1。

设定工况：Y向两直线电机输出相同大小的推力使得工件台在Y向上先加速再减速为零；与此同时工件台在X向上先加速后减速为零。

气浮工件台系统的动态性能主要由气体轴承的各向振动，运动部件绕三坐标轴的偏转误差等因素所决定。其中，气体轴承的振动大小，主要决定了气浮工件台系统的稳定性；绕坐标轴偏转的误差则能体现系统运动的准确性。因此，本文选取气体轴承的气膜厚度和绕Z轴偏转的误差作为仿真对象。仿真结果如图6所示，图6a中纵坐标为承载气体轴承的气膜厚度，横坐标为时间。工件台在运动的初期由于突变力的作用产生上下振动，在气膜阻尼的作用，经过0.35s后气膜厚度值达到稳定值H=1.25×10-5m。这与实际情况相吻合，表明本次仿真结果的正确性。图6b则反映了气浮工件台在上述仿真过程中，滑块绕Z轴偏转的动态误差。

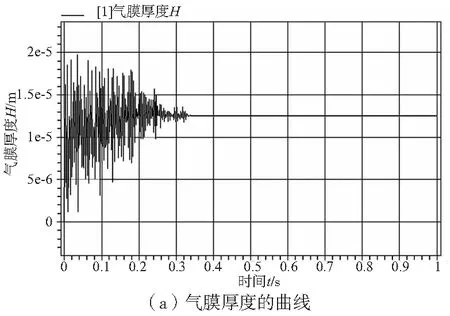
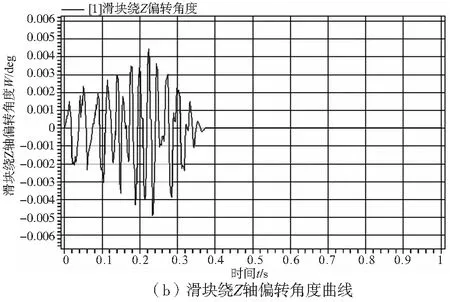
图6 仿真结果曲线

3 工件台设计优化模型

仿真结果如实反应了气浮工件台运动的稳定性和准确性。鉴于气浮工件台运动要求精度高，响应快，有必要在仿真的基础上对气体轴承的垂向振动和绕Z轴的偏转误差进行优化，以提高工件台系统的运动精度。

3.1 优化目标

任务要求工件台在X向和Y向运动时能够以最快的时间达到稳定状态，同时，运动部件绕Z轴偏转的角度值应尽可能地小。具体表现为：系统达到稳定的时间应小于0.25s，而部件绕Z轴偏转的幅值应不大于0.004度。

3.2 设计变量

与工件台系统动态性能相关的独立变量有很多，如何选取对工件台系统性能影响最大的变量进行优化就显得尤为重要。本文采取基于ModelCenter的全因子实验设计(DOE)方法对独立变量进行差分求导数，得到各个变量的灵敏度，从而确定设计变量。图7给出了工件台系统各变量的灵敏度分析结果。根据灵敏度分析的结果最终确定的设计变量有：w1,w2,w3,w4,w6,s1,s2具体各个变量的含义可以参考图2。

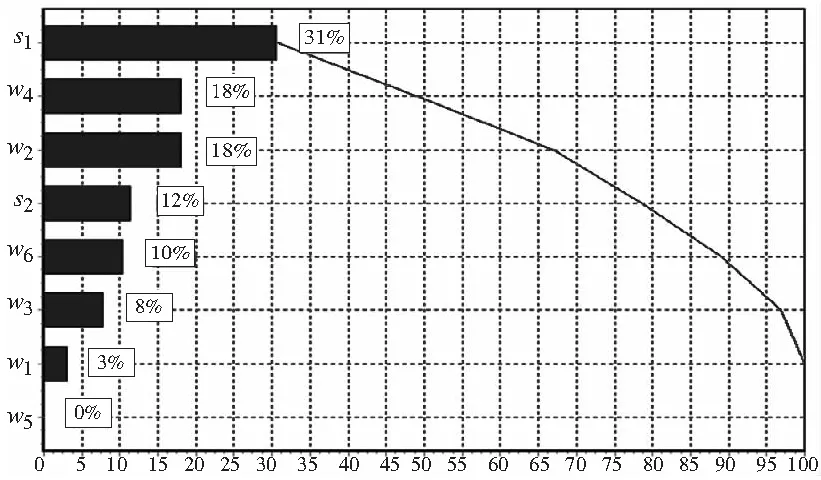
图7 设计变量灵敏度分析

3.3 约束条件

在确定了设计变量后，应该确定相应变量的约束条件。本文所描述的优化问题应满足如下约束条件：各个设计变量的取值区间应同时满足所设定的上下限。同时为了保证气体轴承分布的对称性，应该满足同侧的导向轴承对和承载轴承对的分布距离相同即：

(5)

3.4 数学模型

本文研究的优化问题的数学模型可描述为：

(6)

式中，X——由设计变量组成的列向量；

Wn——权重系数；

Fn——比例因子；

fn(x)——分别代表气膜厚度的最大振动量，运动部件绕Z轴偏转角度值；

Ximin——设计变量的下限约束值；

Ximax——设计变量的上限约束值。

4 优化与分析

采用ModelCenter中基于遗传算法的多目标优化器对模型进行优化，设计变量在优化前后的对比见表3，优化结果如图8所示。

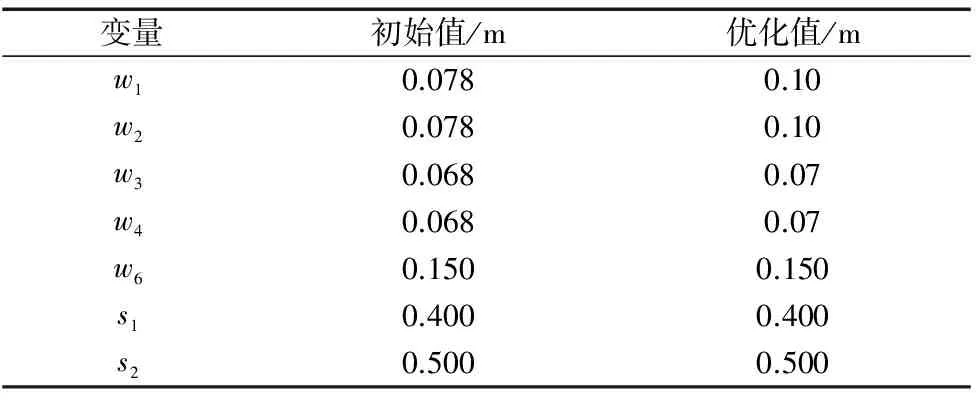
表3 设计变量优化前后对比

从图8a中不难发现，在进行优化后，系统的稳定性显著提高，响应时间明显缩短。相应的图8b中滑块绕Z轴偏转的动态误差也显著减少。

图8 优化结果

5 结论

本文将基于ModelCenter的多学科设计优化方法运用到精密气浮工件台系统的总体设计中，建立了工件台几何模型，直线电机模型，气体轴承模型。并基于ModelCenter进行系统集成，计算出了工件台系统中气膜的振动量以及运动部件绕Z轴的偏转误差。在此基础上，对气体轴承的分布位置进行了参数优化，优化结果显示在相同工况下，气体轴承的气膜厚度达到平衡所需时间由优化前的0.35s左右减少到优化后的0.12s左右；滑块绕Z轴偏转角度的最大值也减少了0.001度左右，比优化前的结果降低了25%。以上分析结果表明优化气体轴承的安装位置可以极大地提高工件台系统的工作性能。 在今后的研究工作中，将进一步研究直线电机以及气体轴承本身的结构设计参数对工件台系统性能的影响。

[1]朱煜，尹文生，段广洪.光刻机超精密工件台研究[J].电子工业专用设备，2004(2)：25-27.

[2]Hiramoto K,Hansed A,Ding S,et al.A study on the drive at center of gravity(DCG) feed principle and its application for development of high performance machine tool system[J].CIRP Annals-Manufacturing Technology,2005,54(1):333-336.

[3]马波琪.精密气浮运动平台动力学建模与动态误差分析[D].武汉：华中科技大学，2011.

[4]陈学东，谢德东，何学明，等.精密气浮直线电机结构动学建模与分析[J].武汉理工大学学报，2008,30(5):117-121.

[5]Chen X D,Yu X Z,He X M ,et al. Dynamic characteristic analysis of precision linear motor with air-bearing in optical lithography[J].Chinese Journal of Mechanical Engineering,2008,21(2):17-22.

[6] Cai Tian,Zhang Ming,Zhu Yu,et al.Dynamic modeling and analysis of a 3-DOF ultra-precision positioning stage with air bearing[J].Procedia Engineering,2011,16,264-270.

[7]张从鹏，刘强.基于静压气浮导轨的直线电机高性能工作台研制[J].机械科学与技术,2006,10(10)：1212-1216.

[8]马继楠，刘莉，龙腾.基于ModelCenter的EPUAV系统模型建立与参数优化[J].系统仿真学报，2009,16(21)：5203-5206.

[9]叶云岳.直线电机原理与应用[M].北京：机械工业出版社，2002.

[10]叶云岳.直线电机技术手册[M].北京：机械工业出版社,2003.

[11]王云飞.气体润滑理论与气体轴承设计[M].北京：机械工业出版社，1999.

(编辑 赵蓉)

System Modeling and Parameters Optimization of Ultra-precision Stage Based on ModelCenter

CHEN Peng-fei , WANG Yan-wei

(CAD Center, Huazhong University of Science&Technology, Wuhan 430074, China)

As the deflection and vibration of the moving components are inevitably incurred in ultra-precision stages,System model of ultra-precision stage was established,including geometry, linear motor and gas-lubricated bearing.The dynamic characteristic of the stage was analyzed through an numerical simulation .Meanwhile, the deflection and vibration evaluation were achieved under given condition,which helped to provide a theoretical reference value for the stage in design.System model of the ultra-precision stage was integrated based on Modelcenter.Optimization model was also established and parameter optimization design of ultra-precision stage was carried on using genetic algorithm.The optimization results meet the design requirement.

ModelCenter;ultra-precision stage; system model;parameter optimization; deflection vibration

1001-2265(2014)04-0026-04

10.13462/j.cnki.mmtamt.2014.04.007

2013-08-20;

2013-09-02

国家自然科学基金项目(51075162, 51375186)； 国家科技重大专项子课题(2011ZX02403-005)

陈鹏飞(1989—)，男，合肥人，华中科技大学硕士研究生，主要研究方向为机械系统CAE， (E-mail) cpfhust@hust.edu.cn。

TH166;TG65

A