基于五次速度曲线的高柔性加减速前看算法*

宁培志,毕庆贞,王宇晗,石 璟

(上海交通大学 机械与动力工程学院，上海 200240)

基于五次速度曲线的高柔性加减速前看算法*

宁培志,毕庆贞,王宇晗,石 璟

(上海交通大学 机械与动力工程学院，上海 200240)

为了减小机床振动，提高连续小线段加工速度，提出了一种基于S型加减速的前看插补算法。采用五次多项式速度曲线，可以实现加速度和跃度的连续变化。首先根据NC代码的目标进给速度、机床动力性能和微段几何特征预求速度约束，然后反向扫描求解满足减速要求的速度约束，最后根据线段长度规划出约束之下的速度曲线，发送至位控模块进行实时运动控制。集成到三轴数控试验平台上试验，算法运行稳定，大大提高衔接速度，仿真结果表明加工时间比传统插补算法缩短了77.31%。

五次多项式;速度规划;高柔性加减速

0 引言

实现对连续小线段的高速高精度加工是当前机床研究的一个重要课题[1]。对CAM软件离散出的微小线段加工时，常规插补器要在每个线段的终点减速到零，频繁启动停止，速度局限在很低的范围内，发挥不出机床应有的性能。而通常的直线加减速会造成加速度的突变，更使得机床的冲击振动加剧，造成加工效率低，表面质量差[1]。因此，消除机床冲击，提高小线段衔接速度是高档机床亟待解决的问题。

为此国内学者对S型加减速和前看算法进行了深入研究[2-6]，同时也采取用Bezier,、B-spline、NURBS等过渡小线段拐角，或者直接拟合线段群来进行速度光顺[6,9-11]。王宇晗等[2]基于直线加减速模型，预处理一定段数，采用循环迭代递归不等式的方法求解约束速度。Leng等[3]提出了一种五次多项式的速度曲线，并根据线段长度分析了单段直线的几种速度轮廓曲线，在前看研究时候却对三次曲线采取先减速点预测再整体跨段加减速的算法[4]。Zhao等[5]将预处理的段数看成是一个浮动窗口，在窗口内进行速度规划，该窗口不断前移推动着前看算法的实施。

本文基于五次多项式的速度曲线进行前看规划，能够实现加速度和跃度的连续变化，消除机床冲击振动，提高段间衔接速度。先介绍了五次速度曲线多项式，根据边界条件推导出计算公式，然后对预处理的线段节点速度进行反向扫描和正向规划，提出了一种优化节点速度的算法。

1 五次多项式速度曲线

1.1 五次多项式曲线公式

为了保证速度、加速度和跃度的连续变化，速度曲线采用五次多项式[3-4]：

V(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5

(1)

对速度进行规划，要满足起始速度为Vs，终止速度为Ve。为了避免相邻速度规划段过渡时的冲击，起始和终止的加速度、跃度都设为0，则边界条件为：

V(ts)=Vs,V(te)=Ve,a(ts)=0,a(te)=0,

J(ts)=0,J(te)=0

记速度规划段持续时间为td，从ts=0到t=te，则td=te-ts；记速度跨度为Vd=Ve-Vs；代入式子(1)则可以得到：

(2)

(3)

考虑机床动力性能约束，加速度和跃度不得超过最大值Am、Jm。对速度函数求导得到加速度和跃度随时间变化的函数，进而可求得该段内加速度、跃度的最值：

(4)

1.2 五次S曲线速度与长度的计算

要发挥机床的最大加速能力实现Vd的速度跨度，根据式(4)取最短时间。一般情况下跃度远远大于加速度的值，即Jm>>Am，所以由Vs到Ve的变速时间为：

(5)

将(5)式中td的值代入(3)式，可得：

(6)

从式(6)可知，若已知要规划始末速度可以直接算出加减速所需要距离；若已知起始速度和线段长度L，所能达到的速度也可以直接算出，计算公式为：

(7)

2 前看多段速度规划

2.1 预求存在的速度约束

段内进给速度在各轴的分量不能超过各个轴的最大速度限制[7]：

段间转向时，速度方向瞬时发生变化会导致各轴速度大小发生变化，要确保不能超过各个轴的最大伺服能力：

由两段夹角大小决定的速度约束：

其中符号代表意义为：

Li：第i段的长度；

Ts：插补周期

ΔΛi：第i段距离在Λ轴的位移分量Λ=X,Y,Z,A,C

VΛmax：Λ轴的最大进给速度

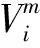
aΛmax：Λ轴允许的最大加速度。

2.2 反向求解满足减速要求的速度限制

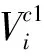
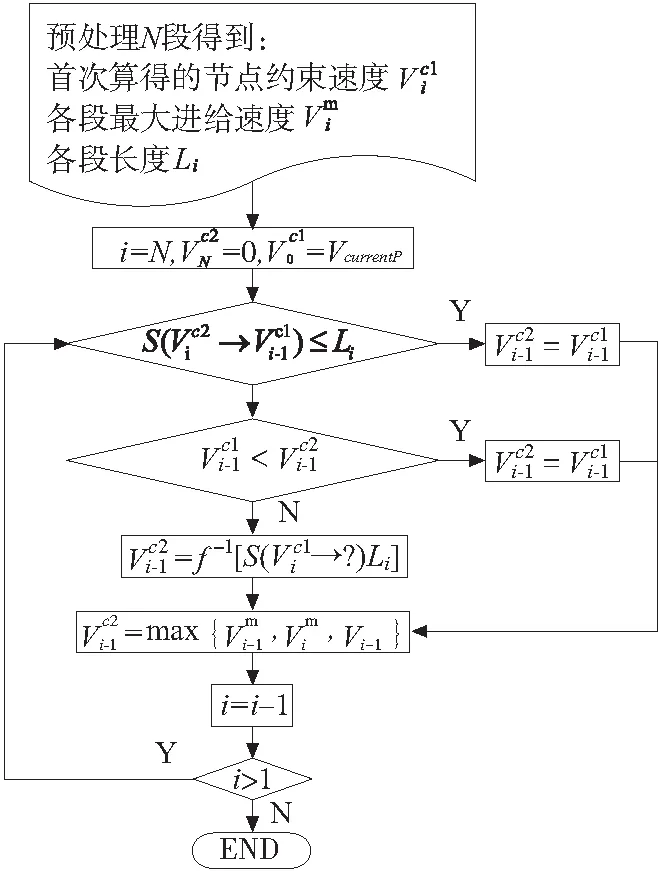
图1 反向求解速度约束流程图

2.3 正向规划速度曲线

在得到满足减速要求的各节点速度约束Vic2之后，开始对预处理的N段进行前看速度规划。根据线段长度、节点速度和段内目标进给速度，正向规流的速度曲线可分为七类：只加速，只减速，加速减速，加速匀速减速，加速匀速，匀速减速，只匀速。流程图如图2，相关公式见1.2节。

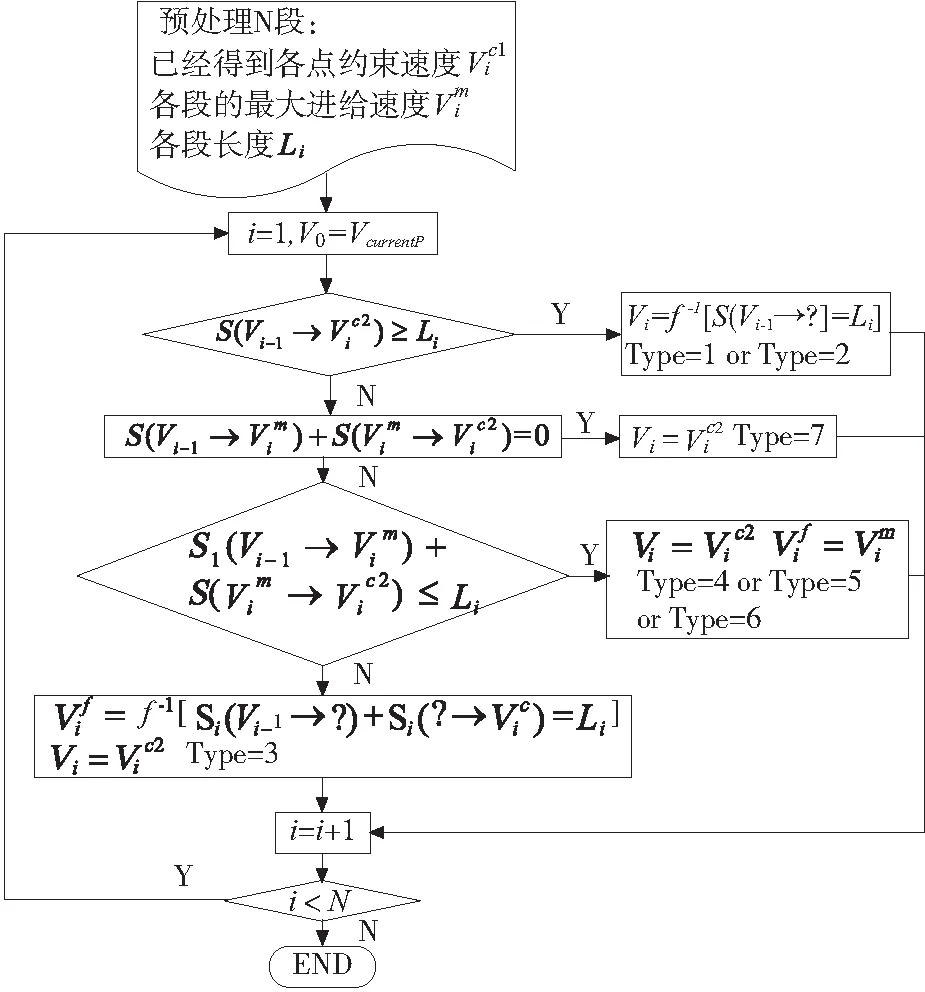
图2 正向前看速度规划流程图

3 数学仿真和机床试验

3.1 数学仿真

为验证算法，对20个随机小线段进行速度规划，各段的长度和各段内进给速度为(mm,mm/s)：0.88/100、1.68/100、1.51/100、0.56/100、1.83/100、0.55/80、1.71/80、0.68/80、0.37/80、2.21/80、2.14/80、0.41/50、1.27/50、0.996/50、0.56/50、0.86/100、0.43/100、0.68/100、1.43/100、3.40/100。用于试验的数控平台参数为：最大速度Vm=100mm/s，最大加速度Am=3000mm/s2，插补周期4ms，最大跃度Jm=106mm/s3。分别前看不同的段数进行仿真，预处理1段(不前看)、2段、4段、8段的速度随时间变化结果如图3。图中横坐标为加工时间，纵坐标为速度，竖直的线为段间分割线也即节点处，水平的线为NC代码的目标进给速度。

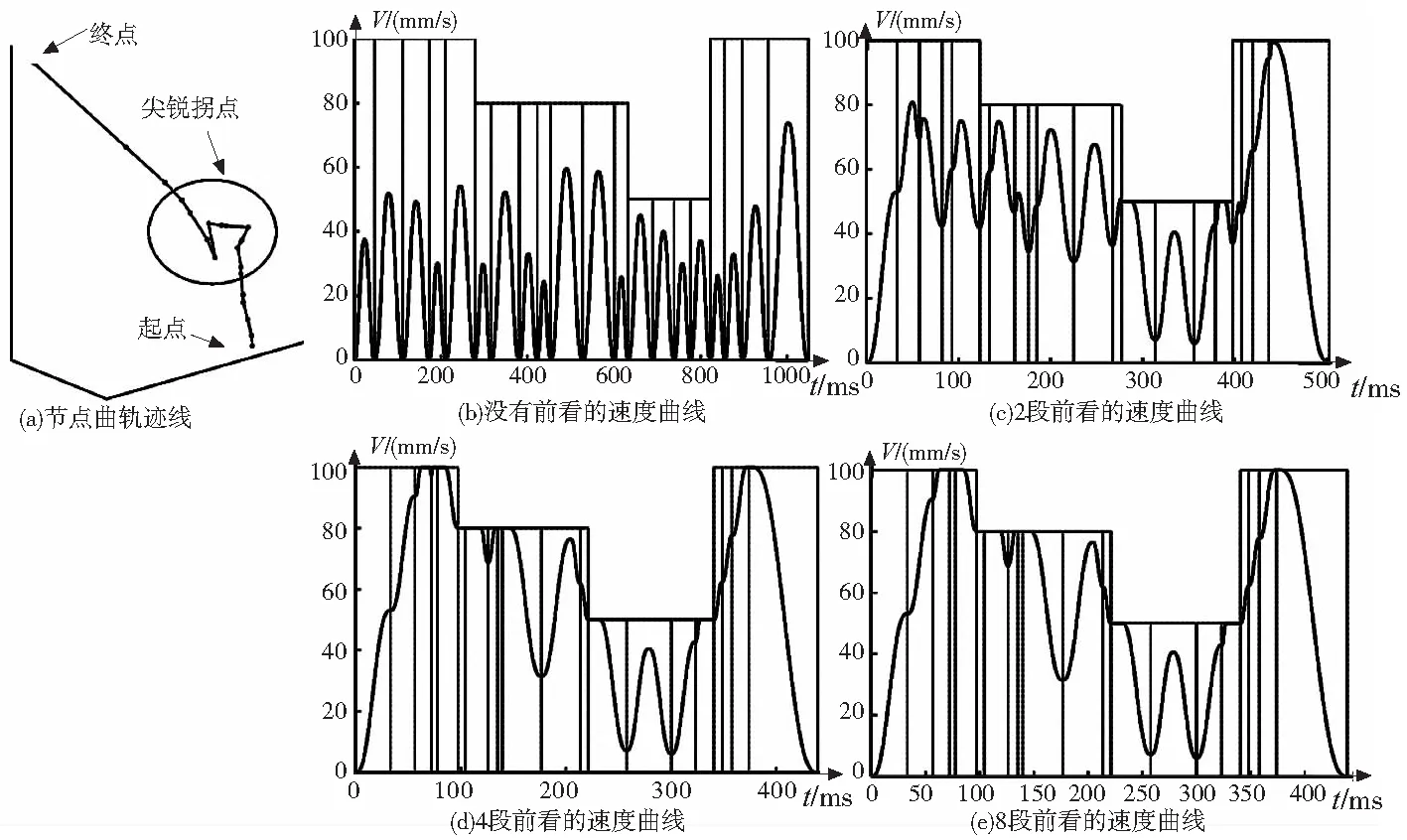
图3 节点轨迹图和前看不同段数的速度曲线图

这些小线段长度在0.3～3mm之间，段间拐角也在6°～180°之间，不同段的进给速度也不尽相同，如图3a。对这些线段处理时，如果不进行前看如图3b，每段结束都将速度减为0，则加工时间为1048.5ms，最大速度大部分在40mm/s以下。每次前看两段的时候如图3c，加工时间为502.7ms，减少了52.1%，最大进给速度也得到提升。当前看4段的时候如图3d，加工时间为439.3ms，最大速度也尽可能的达到了100mm/s。

当再提高前看的段数达到8段时候如图3e，时间已经几乎没有变化，速度曲线也没有更大变化，这是因为中间两个尖锐拐点限制了速度的提升。在一定程度上，前看段数越多效率提高的越多，当达到一定段数之后效率达到最大。考虑到系统计算实时性和存储空间的要求，前看的段数并不是越多越好，段数越多相应算法耗时越长内存要求越大，所以在本算法中采取前看8段。应用前看8段算法对表1的20个线段进行规划，随着每步的前进速度曲线变化如图4所示。

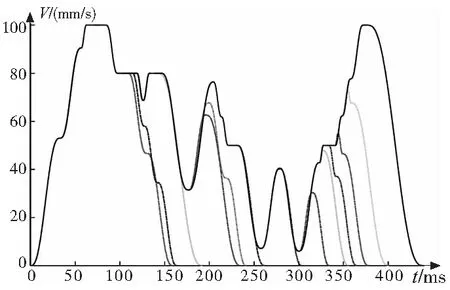
图4 每次前看8段逐步向前推进的速度曲线变化

图5以实例展示了算法每次处理8段逐步前移不断推进的过程。图中虚线表示第一次到达该段时候规划的速度曲线，随着逐段的向前推进会规划出新的速度曲线，更优化的速度会覆盖掉旧的曲线。总体趋势是在不超过速度限制的情况下尽可能提高进给速度，以提高效率。

3.2 机床试验

将前看模块应用到本实验室开放式数控系统试验平台中，加工一个蝴蝶图案，该轮廓是由588个长度在0.02～0.75mm的极小微段组成，如图5。本试验数控平台为自主开发，性能满足基本切削要求：F=3000，Am=0.03×g。仿真结果表明系统不用前看算法的时候加工时间为45.3 s，使用本算法后加工时间为10.3s，效率提高了77.31%，如图6,7所示。

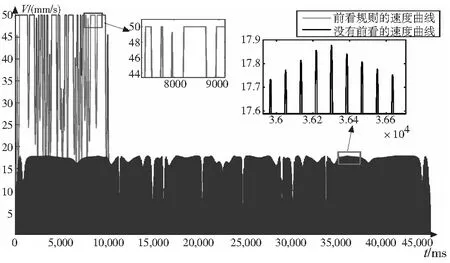
图7 使用前看算法前后速度曲线对比

4 结论

基于五次多项式的速度曲线，提出一种预处理特定段数的前看算法。在前看的段数内先根据机床性能和NC代码编程速度进行速度约束求解，再根据线段长度反向求解满足减速要求的速度约束，然后正向进行速度规划。仿真和试验都证明该算法正确可行，稳定可靠，能大大提高段间衔接速度，进而提高加工效率和表面质量。

[1] 吴祖育, 秦鹏飞. 数控机床[M]. 上海:上海科学技术出版社, 1990.

[2] 王宇晗, 肖凌剑, 曾水生, 等. 小线段高速加工速度衔接数学模型[J]. 上海交通大学学报，2004 , 38 (6) : 901-904.

[3] Leng Hongbin, Wu Yijie, Pan Xiaohong. Research on flexible acceleration and deceleration method of NC system.Technology and Innovation Conference[J].Proceedings of the 2006 International Technology and Innovation Conference, 2006, 524: 1953-1956.

[4] Jin-Hung Chen, Syh-Shiuh Yeh, Jin-Tsu Sun. "An S-curve Acceleration/Deceleration Design for CNC Machine Tools Using Quintic Feedrate Function." Computer-Aided Design& Applications 2011,8(4): 583-592.

[5] 冷洪滨, 邬义杰, 潘晓弘. 三次多项式型微段高速自适应前瞻插补方法[J]. 机械工程学报, 2009, 45(6): 73-79.

[6] Zhao Huan, Zhu Limin, Ding Han. A real-time look-ahead interpolation methodology with curvature-continuous B-spline transition scheme for CNC machining of shortline segments[J], International Journal of Machine Tools & Manufacture, 2013, 65:88-98.

[7] Ming-Tzong Lin, Meng-Shiun Tsai, Hong-Tzong Yau. Development of a dynamics-based NURBS interpolator with real-time look-ahead algorithm[J]. International Journal of Machine Tools & Manufacture, 2007, 47:2246-2262.

[8] Wang Yuhan, Feng Jingchun, Chen Ming, et al, An Optimal Feed Interpolation Algorithm for High-speed Five-axis Machining[J]. Materials Science Forum Vols, 2006, 532-533:873-876.

[9] Bi Q Z, Wang Y H, Zhu L M, et al. Apractical continuous-curvature Bezier transition algorithm for high-speed machining of linear toolpath[J]. Intelligent Robotics and Applications, 2011,465-476.

[10] Haitao Dong, Bing Chen, Youping Chen,et al. An accurate NURBS curve interpolation algorithm with short spline interpolation capacity[J]. The International Journal of Advanced Manufacturing Technology, 2012, 63:1257-1270.

[11] Li Bing Zhang, You Peng You, Jun He, et al. The transition algorithm based on parametric spline curve for high-speed machining of continuous short line segments[J]. The International Journal of Advanced Manufacturing Technology, 2011, 52:245-254.

(编辑 赵蓉)

A High-flexible Acc/Dec Look-ahead Algorithm Based on Quintic Polynomial Feedrate Curve

NING Pei-zhi,BI Qing-zhen,WANG Yu-han,SHI Jing

(School of Mechanical Engineering, Shanghai Jiao Tong University,Shanghai 200240, China)

This paper proposes a interpolation algorithm to reduce vibration and optimize the junction federates between consecutive small line segments. Quintic polynomial is used to ensure the continuities of acceleration and deceleration. First, the algorithm calculates the initial feedrate constraints according to NC code, machine dynamic performance and geometrical characteristic of the lines. Next, the constraints are recalculated from the end of the preprocessing segments so that the feedrate can decelerate to an expected value. At last, the optimized feederate curve is planed regarding the constrains and the lengths of the lines, and the results are sent to the real-time position control module. and reduce the cutting time. When integrated into 3-axis CNC system, simulations indicate that the method can greatly increase the jounction feedrates, and reduce the cutting time by 77.31% compared to the conventional methods.

quintic polynomial;feedrate plan;high-flexible Acc/Dec

1001-2265(2014)04-0015-04

10.13462/j.cnki.mmtamt.2014.04.004

2013-08-05

国家自然科学基金青年科学基金项目(51005155)；中国博士后科学基金特别资助(201104270)；上海市重大技术装备研制专项(ZB-ZBYZ-03-11-2190)

宁培志(1989—), 男, 河南商丘人, 上海交通大学硕士生, 主要从事数控技术和五轴加工研究，(E-mail) ningppz@163.com。

TH166;TG659

A