一个矿产资源的最优价格开采模型研究

王 玲，周 强，李凯鸿，肖海军

(1.武汉职业技术学院，湖北 武汉 430074;2.中国地质大学 数学与物理学院，湖北武汉 430074)

矿产资源的持续利用既是可持续发展战略的重要组成部分，也是可持续发展理论的核心问题之一.矿产资源的最佳耗竭速度的研究为矿产资源的可持续利用提供了相关理论依据.Hotelling［1］的经典论文《可耗竭资源经济学》奠定了非再生资源经济学的基础，开创了可耗竭资源的持续利用研究领域.矿产资源开采的优化目标一般分为两大类［2］:一是局部优化，即使当前开采获得最大利润;二是全局优化，即使开采整个矿床获得最大利润.局部优化是一种仅限于短期利益或个体利益的做法.为了使当前效益获得最大，无论市场价格高低，矿山都尽可能提高开采品位，多采富矿，结果是资源遭受浪费和加速枯竭.全局优化目标的合理性是显而易见的，其最常用的目标是开采整个矿床获得最大的净现值.由于矿产资源的不可再生性及生产对象即矿床的矿化特性，使得矿山开采企业与其它工业企业的生产过程和形式截然不同，一些传统的经济理论的某些方面是难于适用的，因此，理论上就不能简单地从局部优化和全局优化来研究矿产资源开采的优化问题.于是，Dasgupta［3］和Conrad［4］等数理经济学家就从可耗竭资源最佳配置问题进行了深入的研究.文献［5］则又在市场经济条件下，对矿产资源价值与最佳配置问题进行探讨.文献［5］中模型的假设是:在资源寿命期限内，不同的矿产经营主体就各自所允许开采的资源限量已经达成协议(文献［5］的协议形式为每个经营主体开采不同的矿山)，各经营主体不允许侵犯他人的资源开采权.首先，该资源限量协议也不一定能保证所有经营主体在资源寿命期限内获得的经济效益之和达到最大，即当总的资源储量固定时，由于不同经营主体的生产技术、生产成本等因素的不同，存在一个最佳的协议使所有经营主体在资源寿命期限内获得的经济效益之和达到最大.其次，生产者的全局利益最大化可能掩盖了生产者剩余与消费者剩余之间的关系.于是，在文献［6］的基础上，将生产者剩余和消费者剩余引入改进模型，主要工作是从生产者剩余、消费者剩余以及不同偏好下的生产者与消费者剩余总和出发，在矿产资源的最优开采问题中，将生产者剩余与消费者剩余这一永恒的博弈问题转化为优化的决策问题.通过模型的求解，得到资源最优开采的最佳决策方案.

1 基本假设

与文献［6］相同，pt为第t年矿产资源的价格;Q pt()为第t年矿产资源的需求(开采)量，是价格的函数，当价格pt上升时，Qt需求量下降，因此有 dQ/dpt＜0;C Qt( )为成本函数.其满足:当 Qt＞0时，C Qt( )＞0，且dC/dQ＞0，d2C/dQt2＞0，即随着开采量的增大，成本C也随之增加，此外随着开采时间的推移，资源品位不断下降，单位开采成本也越来越大.St为第t年矿产资源的储量;T为该资源耗尽时间;ρ为折现系数，ρ=1/1+r( );r为折现率.

2 系统模型

生产者利润函数:

当价格pt过低时，生产者无利可图，因此存在一个价格，使得π()=0.当价格pt过高，高到人们的最大支付意愿时，资源的开采和消费就会被迫停止.需求被驱逐市场，并被其他代用品所取代，因此存在另一个价格，使得 π()=0.生产者利润也称为生产者剩余，指生产者出售资源Q pt()之后所获得的利润，在研究矿产资源最佳开采利用时不但要考虑生产者利润，同时也要考虑消费者剩余.

消费者愿意花的钱与实际花的钱之差，称为消费者剩余.消费者剩余可以理解为消费者获得的收益，具体表示为:

目标函数中应同时兼顾两者利益，即生产者剩余与消费者剩余总和的现值为最大［5］.

所以目标函数为:

由已知矿产资源开发的特性可得约束条件:

式中t=0为系统的初始时刻;A为初期矿产资源的储量(初始状态已知);St为t期矿产资源的储量，称为状态变量.st+1－st=－Qt(t)(t=0，1，…，T－1)是一组差分方程，给出了状态t到状态t+1的转移规律.

3 模型的改进与求解矿产资源最优价格策略

首先，假设需求函数为:

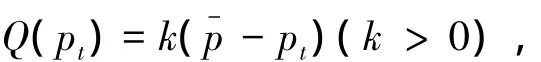
总成本函数为:

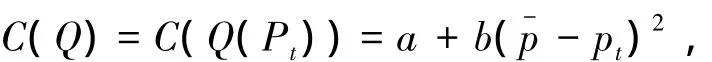
那么，生产者剩余函数为:

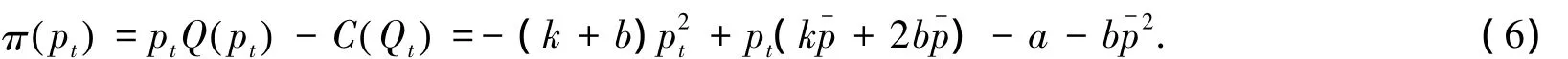
消费者剩余函数为:

由表4表明，试验鹅饲粮中添加不同剂量壳聚糖均能降低血清丙二醛（MDA）含量，1 000 mg/kg壳聚糖组显著低于对照组（P＜0.05），其中500、2 000 mg/kg壳聚糖组均极显著低于对照组（P＜0.01）。除250 mg/kg壳聚糖组略高于对照组外，其它试验组饲料中添加壳聚糖可极显著提高血清超氧化物歧化酶（SOD）活性（P＜0.01）。分析结果同时显示，饲粮中添加500 mg/kg壳聚糖能显著提高试验鹅谷胱甘肽过氧化物酶（GSHPx）活性（P＜0.05），而其它试验组与对照组未见显著差异（P＞0.05）。

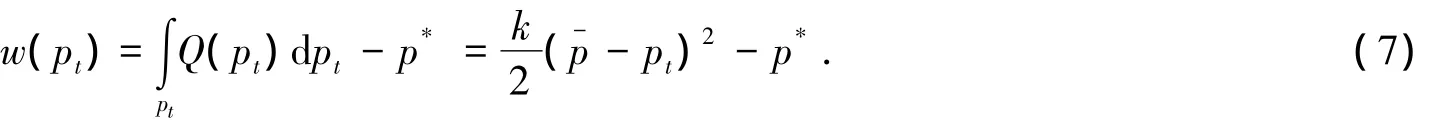
模型(3)是文献［6］研究的主要模型.现对模型(3)稍作修改，即在增加消费者剩余和生产者剩余不同的“偏好”的情形下，对其最佳开采方式进行研究.

模型1 在消费者剩余函数w(pt)至少为c1的前提下，希望生产者剩余函数π( pt)最大.

此时，问题可转化为求最优问题:

再由式(8)、(10)构造拉格朗日函数:

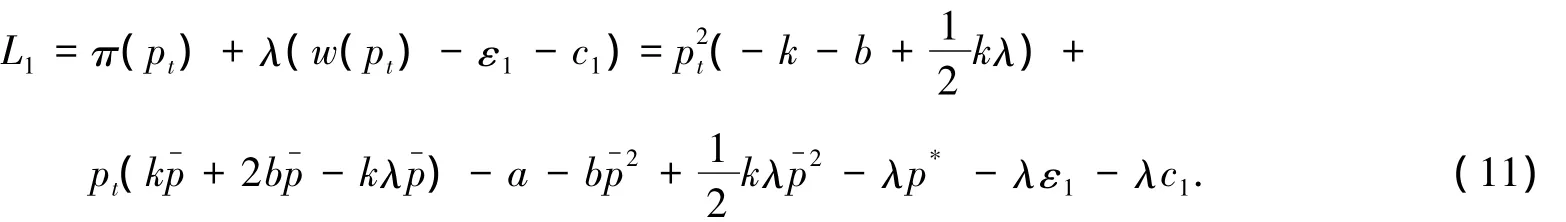
对式(11)分别求导，令:

由方程组(12)解得:

模型2 在生产者剩余函数π( pt)至少为c2的前提下，希望消费者剩余函数w(pt)最大.

此时，问题可转化为求最优问题:

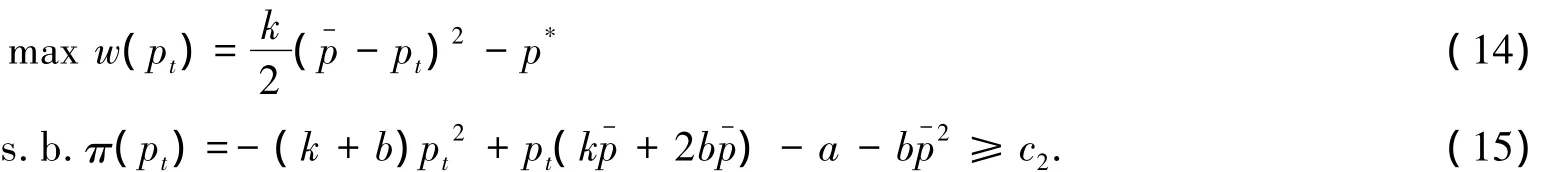
再由式(14)和(16)构造拉格朗日函数:

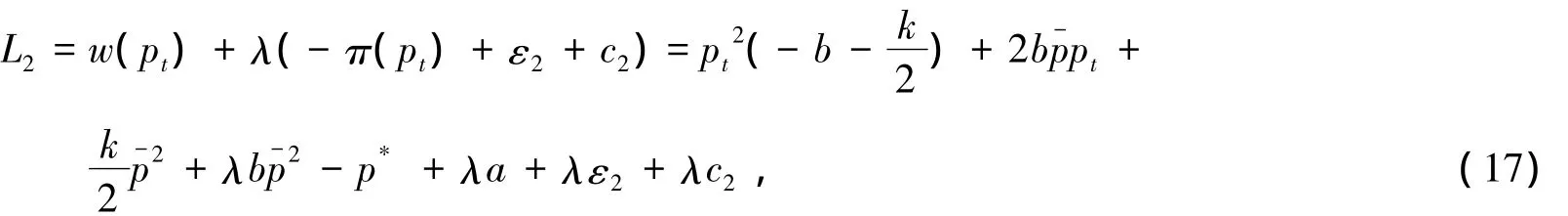
对(17)式分别求导，令:

从方程组(18)解得:

式(20)说明，将生产者剩余控制在某一定水平之下时，消费者剩余可以达到最大.

模型3 针对生产者剩余和消费者剩余的不同“偏好”，希望总剩余最大.

此时，问题可转化为求最优问题:

对式(21)分别求导，令:

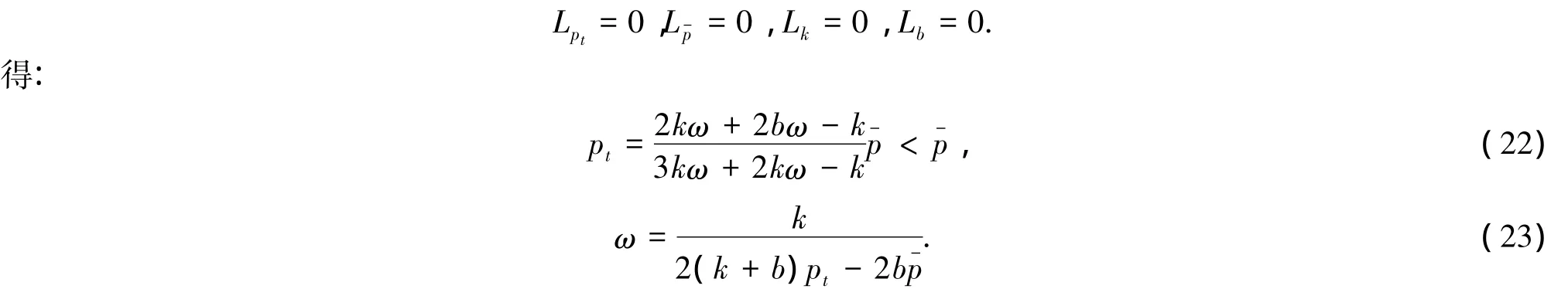
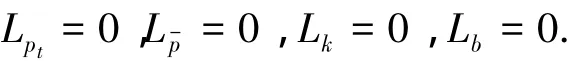
式(23)给出了生产者剩余和消费者剩余总和最大时，矿产资源的生产偏好于消费者的“偏好”大小的计算公式.

4 实证分析

式(21)中的权重系数λ表示消费者剩余与生产者剩余之间的“偏好”.权重系数ω的值越大，说明总剩余源于生产者剩余越大，即生产者剩余占总剩余的比例就越大.此时，矿业生产是“偏好”于矿产企业的;反之，矿业生产“偏好”于消费者.

以汽油价格为例，假定pt表示当前的汽油价格，p－表示人们愿意购买的最大价格.

情形1 假定人们愿意购买汽油的最大市场价格(p－)为5.5元/升，根据式(22)可得市场价格pt与权重系数ω之间的关系，如图1所示.

结论1 汽油的市场价格pt越接近于人们愿意购买的最大价格p－，权重系数ω的值越小，即生产者剩余对总剩余的贡献比例越小，消费者剩余偏大，矿业生产“偏好”于消费者;反之，生产者剩余对总剩余的贡献比例越大，消费者剩余偏小，矿业生产“偏好”于矿产企业.

情形2 假定当前汽油的市场价格pt为6元/升时，根据式(23)可得人们最大可接受价格p－与权重系数ω之间的关系，如图2所示.

结论2 汽油的市场价格pt一定时，人们愿意购买的最大价格p－越接近于市场价格pt，权重系数的值就越大，即生产者剩余对总剩余的贡献比例越大，消费者剩余偏小，矿业生产“偏好”于矿产企业;反之，生产者剩余对总剩余的贡献比例越小，消费者剩余偏大，矿业生产“偏好”于消费者.

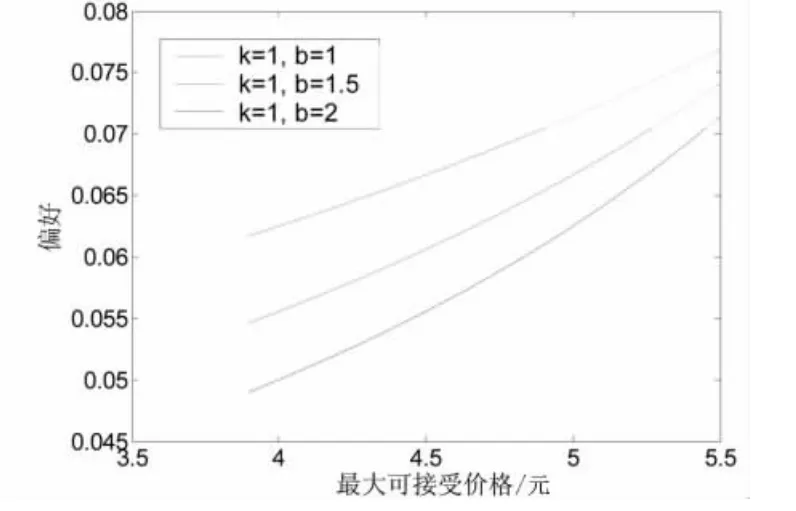
图2 最大可接受价格与利润偏好之间的关系Fig.2 The relationship between the maximum acceptable and prefit preference

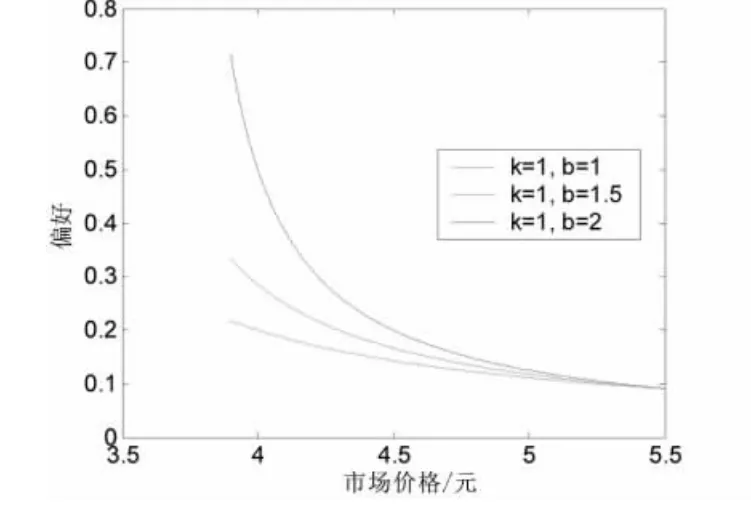
图1 市场价格与利润偏好之间的关系 Fig.1 The relationship between the market price and the profit preference

5 研究的局限性以及后续研究的方向

矿产资源最优开采问题通常研究的是资源利润的最大化问题，它往往取决于资源的开采速度，折现率，市场需求，开采周期和消费者剩余价值等因素，如文献［7－8］所述.但是，在研究资源利润最大化的同时，也有必要对消费者剩余、生产者剩余以及两者的共同剩余等因素进行深入的研究，如本文所述.文章将生产者剩余和消费者剩余引入改进模型，在矿产资源的最优开采问题中，将生产者剩余与消费者剩余这一永恒的博弈问题转化为优化问题.理论研究表明，在消费者剩余首先得到一定保证的前提下，生产者剩余是不可能达到最大.然而，在生产者剩余控制在某一定水平之下时，消费者剩余可以达到最大.最后还得到了两者的共同剩余与不同偏好之间的关系.

当然，在研究资源总剩余最大化的问题时，模型还应该进一步地考虑技术创新、替代资源的发现、资源危机甚至金融危机等突发事件对市场需求的影响，此外，还应考虑勘探活动对于矿产资源价格和开采率的影响.这是都是今后需要进一步研究的问题.

［1］Hotelling H.The economics of exhaustible resources［J］.Journal of Political Economy，1931，39(2):137－175.

［2］任毅，臧维，徐幼林.矿产资源的优化开采经济模型及其求解算法［J］.中国矿业，1998，7(3):60－62.

［3］Dasgupta P S，Heal G M.Economic theory and exhaustible resources［M］.Cambridge:Cambridge University Press，1980:113－176.

［4］Conrad J M，Clark C W.Natural resource economics:notes and problems［M］.Cambridge:Cambridge University Press，1987:122－210.

［5］魏晓平，王立杰.市场经济条件下矿产资源价值与最佳配置研究［J］.系统工程理论与实践，1997(6):26－29.

［6］杨玉凤，魏晓平.市场经济条件下矿产资源最优价格策略研究［J］.中国管理科学，2001，9(4):36－39.

［7］Pindyck，Robert S.The Optimal Exploration and Production of Nonrenewable Resources［J］.Journal of Political Economy，1978，86(5):841－861.

［8］Mueller M J.Behaviour of Non－Renewable Natural Resource Firms Under Uncertainty［J］.Energy Economics，1994，16(1):9－21.