(F,α,ρ,d)-凸性下的非光滑多目标分式规划问题的对偶
姚元金
(吉首大学数学与统计学院,湖南吉首 416000)
在(F,α,ρ,d)-凸性条件下,研究了一类非光滑多目标分式规划问题的对偶问题,给出并证明了该对偶问题的弱对偶定理,强对偶定理和严格逆对偶定理.所得结论改进和推广了相关的结果.
(F,α,ρ,d)-凸;非光滑多目标分式规划;弱对偶定理;强对偶定理;严格逆对偶定理
本文考虑如下多目标分式规划:

其中 X0⊂Rn,fi:X0→R,gi:X0→R,i=1,2,…,p 和 hj:X0→R,j=1,2,…,m,是局部 Lipschitz函数.假定对所有x∈X0,gi(x)>0,i=1,2,…,p.并记可行集为 X={x∈X0|hj(x)≤0,j=1,2,…,m}.
对于多目标分式规划的对偶问题,已有很多文献进行了研究.文献[1]和文献[2]对具有伪不变凸的多目标分式规划问题和(F,ρ)-凸函数的多目标分式规划问题分别给出了相应的对偶定理.文献[3]对(F,ρ)-凸函数的同分母多目标分式规划问题给出了相应的对偶定理.文献[4]和文献[5]对可微的函数引入了(F ,α,ρ,d)-凸和广义 ( F ,α,ρ,d )-凸的概念,并在 ( F ,α,ρ,d )-凸和广义 ( F ,α,ρ,d)-凸性下,获得了一类多目标分式规划的对偶问题的弱对偶定理.
文献[6]建立了(MFP)的一个如下对偶模型:
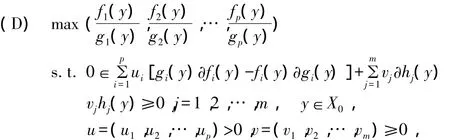
其中∂f(y)为Clarke广义梯度.并对局部Lipschitz函数引入了一类非光滑广义不变凸的概念,并在此条件下,给出并证明了该对偶(D)的弱对偶定理,强对偶定理和严格逆对偶定理.
本文对文献[6]定义的非光滑广义不变凸概念进行推广,定义了一类新的(F,α,ρ,d)-凸性概念,然后在此凸性条件下给出并证明了该对偶(D)的弱对偶定理,强对偶定理和严格逆对偶定理.改进和推广了文献[6]的相应结果.
1 预备知识
设 X0⊂Rn.对 x=(x1,x2,…,xn)∈X0和 y=(y1,y2,…,yn)∈X0,约定:

定义1[7]设有实值函数f:Rn→R,若对正常数k和z的一个邻域N使得对任何x,y∈N有:|f(x)-f(y)|≤k||x-y||,则称函数 f:Rn→R 是局部 Lipschitz的,其中||·||为 Rn中的范数.对于局部Lipschitz函数f(x),Clarke[7]曾经给出如下广义方向导数和广义梯度概念:
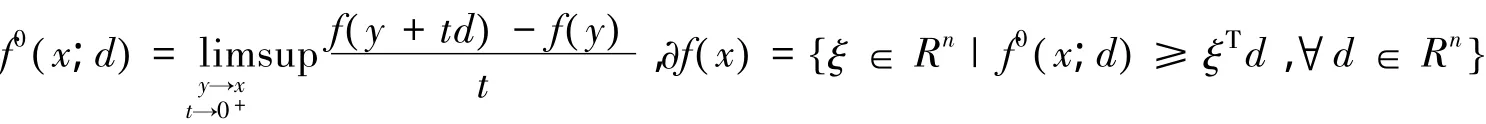
引理1[7](1)∂f(x)是非空凸紧集;(2)∂(-f(x))= -∂f(x);(3)∂(f+g)(x)⊆∂f(x)+∂g(x).
定义 2[8]称函数 F:X0×X0×Rn→R 为次线性的,若对任何 x,y∈X0,有:
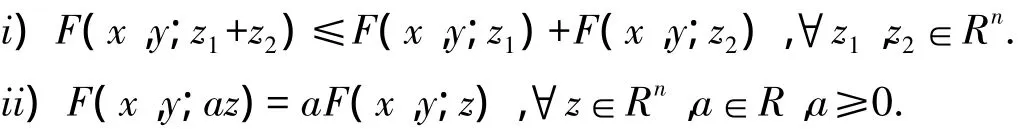
以下均设 X0⊂Rn,函数 F:X0×X0×Rn→R 为次线性的.
定义3 称局部 Lipschitz函数 f(x):X0→R 为在∈X0处是(F,α,ρ,d)-凸的,若存在函数 α:X0×X0→R+{0}和 d:X0×X0→R 以及 ρ∈R,使得∀x∈X0和∀ξ∈∂f(x-),有:

为了给出对偶(D)的强对偶定理,需要先考虑如下规划(EFPk):


引理 2[6]设是(MFP)的有效解且对每个 k∈{1,2,…,p},(EFP)的约束在处满足约束规格 B,则


2 对偶定理
定理1(弱对偶定理)设x是(MFP)的任一可行解,(y,u,v)是(D)的任一可行解,且∀x∈X0、∀i∈{1,2,…,p}、∀j∈{1,2,…,m},若下面条件之一成立:



[1]Liu J C.Optimality and duality for multiobjective fractional programming involving nonsmooth pseudoinvex functions[J].Optimization,1996,37:27-39.
[2]Liu J C.Optimality and duality for multiobjective fractional programming involving nonsmooth(F,ρ)convex functions[J].Optimization,1996,36:333-346.
[3]Chen X H.Optimization and duality theorem for multiobjective fractional programming with the generalized(F,ρ)convexity[J].Journal of Mathematical Analysis and Applications,2002,273:190-205.
[4]曾德胜,吴泽忠.(F,α,ρ,d)-凸和广义(F,α,ρ,d)-凸性下一类多目标规划问题的对偶[J].四川师范大学学报,2006,29(1):63-66.
[5]吴泽忠.广义(F,α,ρ,d)-凸性下一类多目标规划问题的对偶[J].经济数学,2006,23(3):320-324.
[6]姚元金.一类非凸非光滑多目标分式规划问题的对偶[J].西南大学学报,2010,32(3):10-14.
[7]Clarke F H.Optimization and nonsmooth analysis[M].New York:Wiley-Interscience,1983.
[8]Preta V.On efficiency and duality for multiobjective programs[J].Journal of Mathematical Analysis and Applications,1992,166(2):356-377.

