希尔排序效率的真实性拟合尝试——Sedgewick增量序列(1982)

胡圣荣

(华南农业大学 工程学院，广东 广州 510642)

希尔排序效率的真实性拟合尝试
——Sedgewick增量序列(1982)

胡圣荣

(华南农业大学 工程学院，广东 广州 510642)

为了对复杂性未知的希尔排序算法进行合理、可信的数值估计，提出拟合不变性结合拟合准确性和显著性的拟合思想和方法，并对采用Sedgewick增量序列4*22i+3*2i+1的希尔排序算法的平均比较次数进行了数值估计，从cnαlnβ(n)形式开始，在规模为104～108的测试数据的不同区段分别拟合，根据拟合参数的变动特点，进行合理推断并再次拟合及验证，从而逐步分离和确定出α=1,c=1,β=1.41，最终获得了对各区段拟合几乎不变的结果nln1.41(n).拟合方法本身的正确性用已知结果的排序数据进行了验证.

排序；希尔排序；算法；拟合；拟合不变性

0 引言

自从1959年D.L.Shell提出希尔排序算法[1]以来，该类算法的理论分析一直都没有很好解决[2]，有关研究大致有三方面：①理论上下限估计，如文献[3]；②数值估计，如文献[4-6]；③最优增量研究，如文献[7].一般地，对具体的增量序列，除少数特殊情况外都没有理论结果，通常进行数值估计，即采用大量随机输入，对输出结果平均后进行数据拟合.作者发现，这些数值估计，纯粹也只能看做已有数据的一个外在的经验公式，并不代表数据内部的真实变化规律.比如，增加新的数据点，特别是规模更大的新数据点后，新的拟合结果(公式中的有关系数等)一般会有明显变动，而实际的平均复杂性应该是规模的一个确定不变的函数关系.

本文试图从实验数据中得到比较可信的有可能反映真实规律的拟合结果，介绍了拟合原理和方法，对Sedgewick增量序列(1982)的拟合结果具有很好的拟合不变性.

1 拟合思想与方法

1.1 拟合准确性

所见文献一般是对测试数据，按一定的拟合式进行一次性的拟合，主要考察拟合的准确性.如对采用Hibbard序列2t-1，即1, 3, 7, 15, 31, …和Knuth序列(3t-1)/2，即1,4,13,40,121,…的希尔排序，Knuth采用cnα形式拟合，M.A.Weiss采用c1n5/4+c2n+c3n3/4+c4n2/4+c5n1/4+c6形式，后者比前者准确[5].Cotta用an2+bn和anb都能很好拟合Knuth序列[6].显然，采用不同的拟合式必将得到不同的结果，其中总有可能找到比当前更准确的，特别地，采用插值多项式可通过所有样点，但这显然并不意味着“最准确”.

表1 快速排序的平均比较次数 /106

那么，对同一数据的多种拟合，如何判断谁更“真实”呢？作者在文献[8]中提出过一个观点：拟合准确性不一定代表真实性.以快速排序为例，表1为某快速排序算法(快速排序有多种实现)对1000组随机序列排序后的平均结果.

对此数据，发现很多拟合式都能很好地吻合，如y=cnα、cnαlnβ(n)ln[ln(n)]、cnαlnβ(n)、cnln(n)、cnαln(n)、cnln(n)等(转换为适当形式后进行线性拟合).拟合后分别求出y-yi，依次为149.91、0.612 05、0.632 00、14.752、24.584、8.959 1，其中形式较复杂的cnαlnβ(n)ln[ln(n)]拟合误差最小，而较接近理论结果的cnln(n)并不是很好.所以拟合“准确”不一定真实，反之，拟合不太精确的曲线，未必不真实.当然，准确性明显较差的形式cnα优先值得怀疑.

1.2 拟合显著性

另一方面，从统计学观点看，拟合还有一个显著性的问题[9]，一般考察拟合参数的t值、P值和总体结果的R2、AdjustedR2、F值、SignificanceF等，其中t值和F值越大越好，P值和SignificanceF越小越好，R2越接近1越好.

这里进一步指出：拟合显著性也不一定代表真实性.比如SignificanceF，上面6个拟合的结果分别为6.529 8E-16、7.046 8E-21、3.230 2E-25、1.882 8E-15、3.336 1E-21、8.389 4E-22，它们都很显著，其中最显著的是cnαlnβ(n)(此时α=0.992 20、β=1.194 8)，但它并不比cnlnβ(n)(此时β=1.0067)更真实，因为快速排序的理论结果为O(nln(n)).当然，拟合参数明显不显著的cnαlnβ(n)ln[ln(n)](其中ln(c)、的P值为0.148 79和0.641 23较大，而其它几个拟合式的参数P值至少在10-7以下)优先值得怀疑(增加更多数据点拟合会显著些).

1.3 拟合稳定性

为了判断拟合式的真实性，作者在文献[8]提出拟合不变性的思想，即若该拟合式是真实的，则它在数据点的各子区间应该有几乎相同的拟合结果.这是必要条件，但显然没有该特点的拟合，真实性值得怀疑.

为了获得拟合不变的结果，需要将数据分段，再分别拟合.根据各段上拟合参数表现出的特点，进行合理推断以去除数据的“毛刺”(波动)，得到简化形式，然后再次拟合并验证(参数是否稳定、拟合是否显著等).这个过程可能要反复多次，具体实施时还可结合拟合准确性和显著性进行.按此思想，文献[8]对采用Hibbard序列和Knuth序列的希尔排序，拟合结果分别为cn1.26ln-0.5(n)和cn1.25ln-0.5(n)，特别地，当规模n不是很大时，近似为(n1.26)和(n1.25)，这便是Knuth和M.A.Weiss的结果[5].

表2 希尔排序的平均比较次数 /106

表3 区间分段情况

2 拟合过程

Sedgewick在1982年设计了一个增量序列4*22i+3*2i+1(i≥0)，即1, 8, 23, 77, 281, …，效果优于Hibbard序列和Knuth序列，上界为O(n4/3)[2]，但具体平均情况未知.这里取该增量序列进行希尔排序.因测试规模大，测试序列长，为避免序列数据重复(C/C++系统的随机函数rand()只生成0～327 67的随机数)，随机序列的生成采用文献[10]的长周期随机函数，但与之不同的是，这里不通过改变种子来获得不同序列，而是在长周期随机序列中依次截取所需长度的子序列；测试组数也自动选取：最多106组，以当前规模总排序时间不超过1 min为准(该时间根据硬件条件设置)但最少10组.测试结果见表2.

区间分段如下：分别从低到高分4段、2段、1段，见表3所示.其中区段A、B、C、D可考察规模增加时拟合参数是否稳定以及变化趋势，其它几段可考察数据点增加时拟合参数是否稳定以及变化趋势.

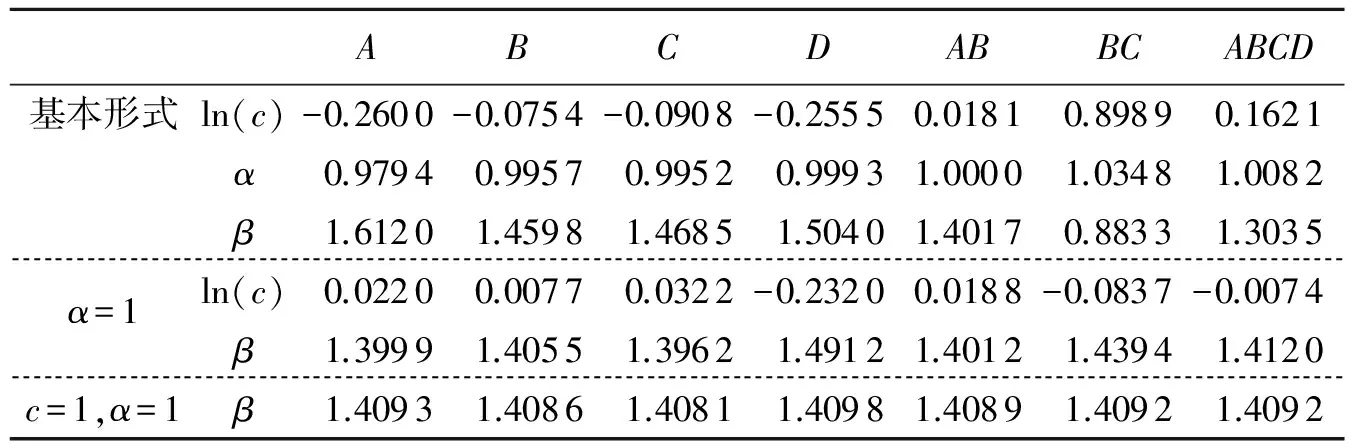
表4 分段拟合及参数的确定(表2数据)

下面对各段分别拟合.由于增量序列有按几何级数变化的特点或趋势，根据文献[8]的思想，拟合形式仍取为cnαlnβ(n)，拟合结果见表4中的基本形式.

从表4基本形式的结果看到，各区段上参数ln(c)变动较大、β次之，而α较稳定，基本在1上下，于是推测α=1，重新拟合，结果见表4中α=1部分.这时参数β也较稳定了，而ln(c)基本在0附近变动(即c接近1)，再次推测c=1后重新拟合，结果见表4最后一行.这时参数β非常稳定，约1.408～1.409.

以上区间分段似乎较特殊，实际上其它分段结果都类似，如改变段的开始、改变段的长度等(数据略).另外，对数据序列细化，如1，1.778，3.162，5.623，10，…，以及其它数据序列，如1，2，4，6，8，10，…，结果也类似(数据略，故本文表2仅取了少量数据).

至于拟合的显著性，表4涉及的3个拟合式(即cnαlnβ(n)、cnlnβ(n)、nlnβ(n))都很显著，如对全段拟合的SignificanceF分别为3.075 7E-20、2.100 4E-15、5.069 4E-23.

综合以上分析，表2数据的最终拟合结果为y=nln1.41(n).

表5 直接插入排序的平均比较次数 /106

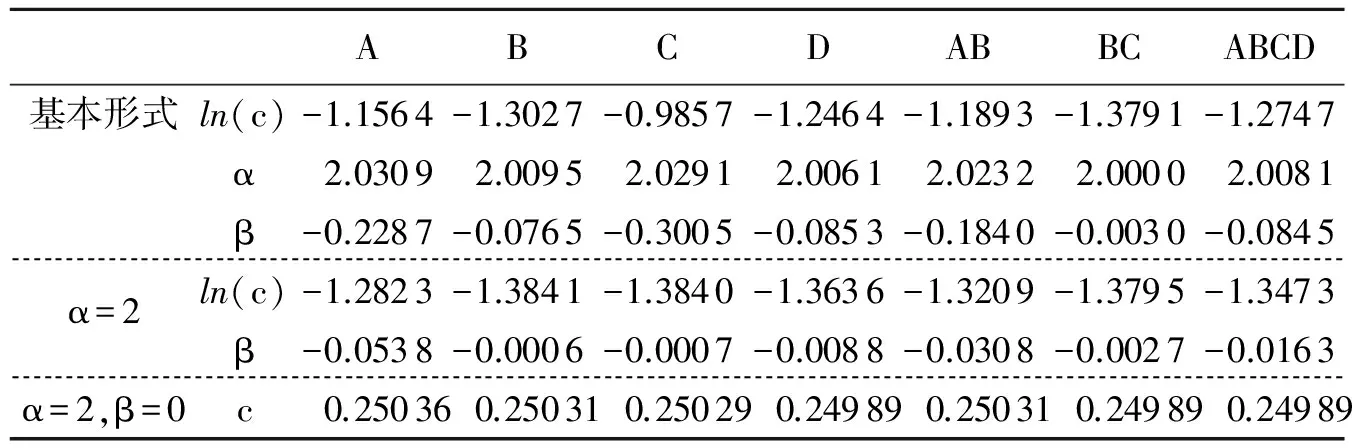
表6 分段拟合及参数的确定(表5数据)

3 拟合方法的验证

下面用已知结果的数据来验证一下上述拟合方法.对表1快速排序的不变性拟合略为繁琐一些，它需要两项形式y=cnαlnβ(n)+n才能稳定，这种情况拟另文介绍.作者发现，简单排序都能一项稳定拟合.以直接插入排序为例，数据见表5.该排序效率低，规模大时排序时间太长，故测试时所取数据组数依次递减：规模量级为102、103、104、105、106时分别取10 000、1 000、1 000、100、1组.仍从cnαlnβ(n)形式开始，拟合结果见表6.

具体过程是，先由基本形式的拟合结果估计α=2；令α=2重新拟合后估计β=0；最后令α=2,β=0再拟合，结果参数c非常稳定，约0.250最后结果为0.250 n2，而理论结果是n(n-1)/40.25 n2.这个过程与表4几乎一样.

4 结论

希尔排序的平均复杂性是规模n的某个确定函数，如果拟合结果是真实的，则它在各数据区段上应该有几乎相同的拟合结果.拟合不变性思想对判断或推测拟合真实性提供了一种值得尝试的可行的方法.

对采用Sedgewick增量序列4*22i+3*2i+1的希尔排序算法，本文的拟合结果nln1.41(n)具有很好的拟合不变性和显著性，虽仍属经验估计，但很可能比其它结果更接近真实.

下一步的工作是探讨合适的其它拟合式及组合拟合式，因为作者的工作表明拟合式cnαln(n)对其它几个测试序列不像本文这样稳定(即使增量类似，但Pratt序列[2-3]除外，对其拟合时很稳定并能得到理论值cnln2(n)[3]，数据略).当然，也可能出现几个拟合式都较稳定如何分辨的问题.另一个要做的工作是对稳定拟合结果的理论证明.

[1]ShellDL.Ahigh-speedsortingprocedure[J].CommunicationsoftheACM,1959,2(7):30-32.

[2]SedgewickR.AnalysisofShellsortandRelatedAlgorithms[J].EuropeanSymposiumonAlgorithms,1996:1-11.

[3]JiangT,LiM,VitányiP.Alowerboundontheaverage-casecomplexityofShellsort[J].JACM,2000,47(5):905-911.

[4]SandersP,FleischerR.Asymptoticcomplexityfromexperiments?Acasestudyforrandomizedalgorithms[C]//AlgorithmEngineering,SpringerBerlinHeidelberg,2001:135-146.

[5]WeissMA.ShortNoteEmpiricalstudyoftheexpectedrunningtimeofShellsort[J].TheComputerJournal,1991,34(1):88-91.

[6]CottaC,MoscatoP.Amixedevolutionary-statisticalanalysisofanalgorithm'scomplexity[J].AppliedMathematicsLetters,2003,16(1):41-47.

[7]CiuraM.Bestincrementsfortheaveragecaseofshellsort[J].Lecturenotesincomputerscience,2001:106-117.

[8]胡圣荣.关于排序效率的数值估计[J].广州城市职业学院学报,2008,2(1):61-64.

[9]何晓群，刘文卿.应用回归分析[M].北京：中国人民大学出版社，2001.

[10]胡圣荣.关于排序算法的随机输入序列[J].武汉理工大学学报,2006,28(9):105-107.

责任编辑：时凌

AttemptatCredibleEmpiricalStudyofShellsort——Sedgewick′s Increment Sequence in 1982

HU Shengrong

(College of Engineering,South China Agricultural University,Guangzhou 510642,China)

In order to estimate unknown complexity of Shellsort reasonably and credibly,this paper suggested combination of fitting invariability with fitting precision and significance, and accordingly the average number of comparisons of Shellsort with Sedgewick′s increment sequence 4*22i+3*2i+1 was obtained about tonln1.41(n),which was originated fromcnαlnβ(n),with parameter inferring from its appearance in different data segments among size of 104to 108,refitting and validating , the values ofα=1,c=1,β=1.41 were determined progressively. The correctness of the fitting method proposed was verified by data with known complexity.

sort; shellsort; algorithm;fit;fitting invariability

2014-05-26.

胡圣荣(1967- )，男，博士，教授，主要从事计算机数值计算相关问题研究.

TP311.12

A

1008-8423(2014)02-0218-04