Boussinesq-burgers方程的对称性约化
房春梅,樊彩虹
(集宁师范学院 数学系,内蒙古 乌兰察布 012000)
Boussinesq-burgers方程的对称性约化
房春梅,樊彩虹
(集宁师范学院 数学系,内蒙古 乌兰察布 012000)
扩展齐次平衡法是求孤子方程的Backlund变换、对称性约化、精确解的一种简单有效的方法,该方法的思想是将高维的偏微分方程约化为低维的常微分方程.根据此方法获得了Boussinesq-burgers方程的新的对称性约化及相似解.
扩展齐次平衡法;Boussinesq-burgers方程;对称性约化
求非线性偏微分方程(组)的对称约化方法很多,如Lie对称方法[1]、Clarkson-kruskal(CK直接方法)[2-3]、扩展齐次平衡法[4-5]等等.本文将扩展齐次平衡法推广应用到Boussinesq-burgers方程[6]:
获得了该方程的新的对称性约化与相似解.
对于Boussinesq-burgers方程,文献[6]讨论了其Painleve可积性,文献[7-8]讨论了该方程基本的Darboux变换.文献[9]获得了无限维的可积系统,进一步得出了(2+1)维Boussinesq-burgers方程的准周期解.
本文将扩展齐次平衡法应用到Boussinesq-burgers方程中,获得了此方程的新的对称性约化以及相似解.
1 Boussinesq-burgers方程的对称性约化与相似解
Boussineq-Burgers方程:
(1)
根据扩展齐次平衡法的思想,对方程(1)可以寻找如下形式的对称性约化:
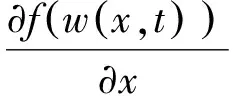
(2)
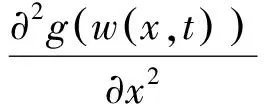
(3)
其中u0,v0是两个待定函数.
将式(2)~(3)代入式(1)可得到:
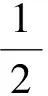
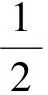
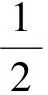
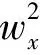
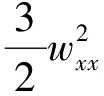
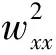
要使上两式约化成f,g关于w的常微分方程,那么f,g的不同导数系数之比仅是关于w的函数,换句话说就是满足下面的限制条件:
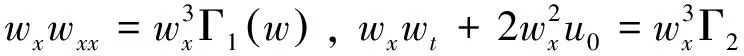
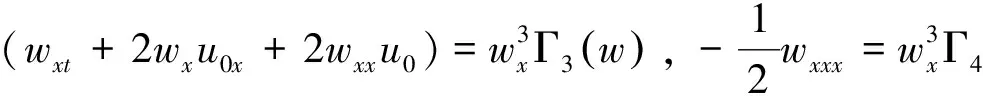
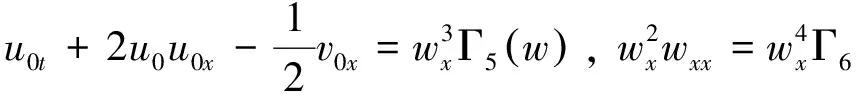
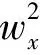
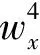
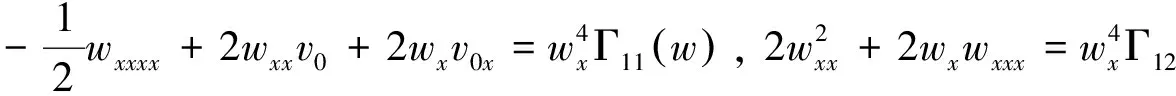
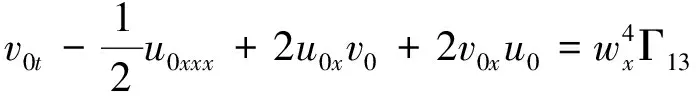
其中Γi(w)(i=1,2,…,13)为待定函数.
求解上述方程时,可以利用下面的三个自由度:
1)如果w(x,t)是由方程Ω1(w)=w0(x,t)所确定,可以取Ω1(w)=w(x,t).
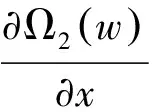
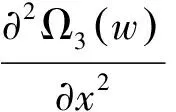
利用上述规则可以得出上述限制条件的解为:
Γ1=Γ2=Γ3=Γ4=Γ6=Γ8=Γ9=Γ10=Γ11=Γ12=Γ13=0,
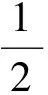
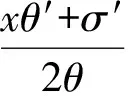
其中θ=θ(t),σ=σ(t)满足如下的方程组:
σ″-2σ′Aθ2=θ4(A2σ-2B),θ′=Aθ3.
且A,B是任意常数.
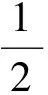
若取f′=R,g″=S,则可得到式(1)如下的对称性约化及相似解:
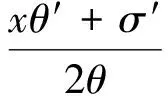
[1]Rodica Cimpoiasu,Rodu Constantinescu.Lie symmetries and invariants for a 2D nonlinear heat equation[J].Nonlinear Analysis,2008,68:2261-2268.
[2]范恩贵.二类变式Boussinesq方程的对称性约化和精确解[J].数学物理学报,1999,19(4):373-378.
[3]楼森岳,唐晓艳.非线性数学物理方法[M].北京:科学出版社,2006.
[4]范恩贵,张鸿庆.齐次平衡法若干新的应用[J].数学物理学报,1997,19(3):286-292.
[5]Fan E G,Zhang H Q.A new approach to Backlund transformation of nonlinear evolution equations[J].Appl Math Mech,1998,19(7):645-650.
[6]Sachs R l.On the Integrable Variant of the Boussinesq System:Painleve Property,Rational Solutions[J].Physica D,1988,30:1-27.
[7]Matveev V B,Salle M A.Darboux Transformations and Soliton[M].Berlin:Springger,1991.
[8]展红霞.Boussinesq-burgers方程的各类达布变换关系及其精确解[J].辽宁工业大学学报,2010(8):265-269.
[9]Zhang J,Wu Y,Li X.Quasi-Periodic solution of the (2+1)-dimensional Boussines q-Burgers soliton equation[J].Physica A,2003,319:213-232.
责任编辑:时凌
SymmetryReductionsoftheBoussinesq-burgersEquation
FANG Chunmei,FAN Caihong
(Department of Mathematics,Jining Teachers College,Wulanchabu 012000,China)
The extended homogeneous balance method is mainly used for finding the Backlund transformation,symmetry reduction and exact solutions of nonlinear evolution equations.The idea of the method is to reduce the high dimensional partial differential to a low-dimensional ordinary differential equation. Based on this method, the new symmetry reduction and solution of the Boussinesq-burgers equation are obtained.
extended homogeneous balance method; Boussinesq-burgers equation; symmetry reduction
2014-04-01.
内蒙古高等学校科学研究资助项目(NJZC13283)
房春梅(1985- ),女(蒙古族), 硕士生,主要从事孤子方程与可积系统的研究.
O290
A
1008-8423(2014)02-0148-02
——评《食品安全治理的中国策》

