双材料反平面非对称界面端研究

赵 绚，杨 林，王小丽，李俊林

(1.运城师范高等专科学校数学与计算机系，山西运城 044000;2.太原科技大学运城工学院基础部，山西运城 044000;3.太原科技大学应用科学学院，山西太原 030024)

文献［1－3］给出了正交异性双材料反平面(对称)界面裂纹的理论分析与研究，并求解出了相应的应力场、位移场及应力强度因子的解析表达式.文献［4－6］给出了正交异性双材料半无限裂纹界面裂纹理论分析.文献［7－8］给出了反平面界面端应力强度因子经验公式及实验结论.本文研究了正交异性双材料非对称反平面的界面端问题，通过构造了应力函数，并结合复变方法，在给定的自由边界及连续条件下，得到了一组四阶齐次线性方程组，从而求解出了正交异性双材料非对称反平面界面端的特征方程，并对特征值λ的变换规律做出了相应的研究.

1 反平面撕开型力学模型

如图1所示，λ为两种不同的材料粘接界面.θ2为第1类正交异性的复合材料，其中复合材料的工程常数为φj(j=1，2)，y＜0为第2类正交异性的复合材料，其复合材料工的程常数是(G23)2，(G31)2.

在反平面撕开型，即III型裂纹中，位移表示如下:

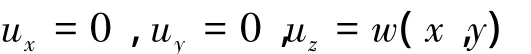
而对正交异性双材料来说，假设材料的弹性主轴与坐标轴是重合的，则由其物理方程得到相应的应力分量:

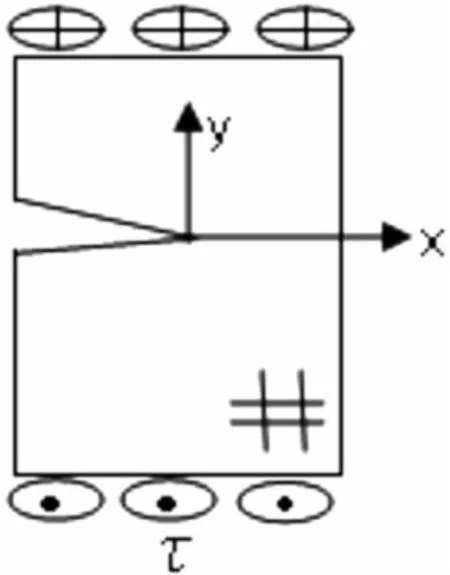
图1 III裂纹Fig.1 III model interface crack

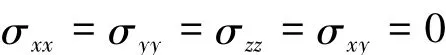
由弹性力学知道，此控制方程为:

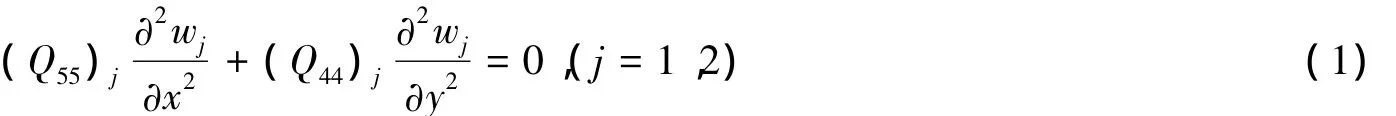
整理式(1)可得到:

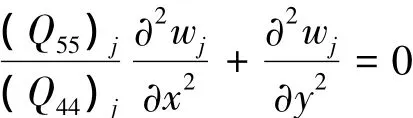
由弹性力学得到，其相应的应力分量为:

其中:r和 θ为从裂纹边缘起度量的极坐标.而常数(Q44)j=(G23)j，(Q55)j=(G31)j;(G23)j，(G31)j(j=1，2)是材料的剪切模量.

2 给定的自由边界条件及连续条件

如图1所示，此图为正交异性双材料反平面界面端的问题，其界面连续条件及自由边界条件可表示为:

设位移为wj=wj(x+sjy)，wj(x+sjy)对固定的j是任一复变函数.

将wj(x+sjy)代入控制方程(1)，得到特征方程:

定义Δj=－(Q44)j(Q55)j，方程(7)有两对共轭虚根，取其虚部大于零的根如下:

3 界面裂纹的特征方程

假设应力函数为:

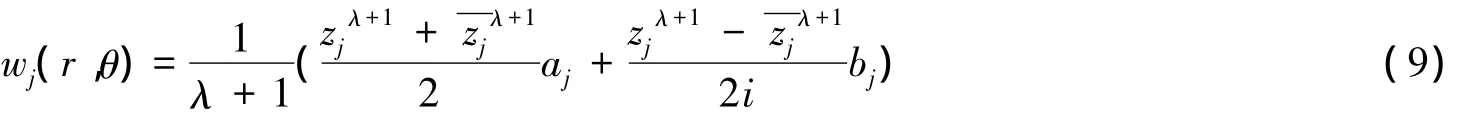
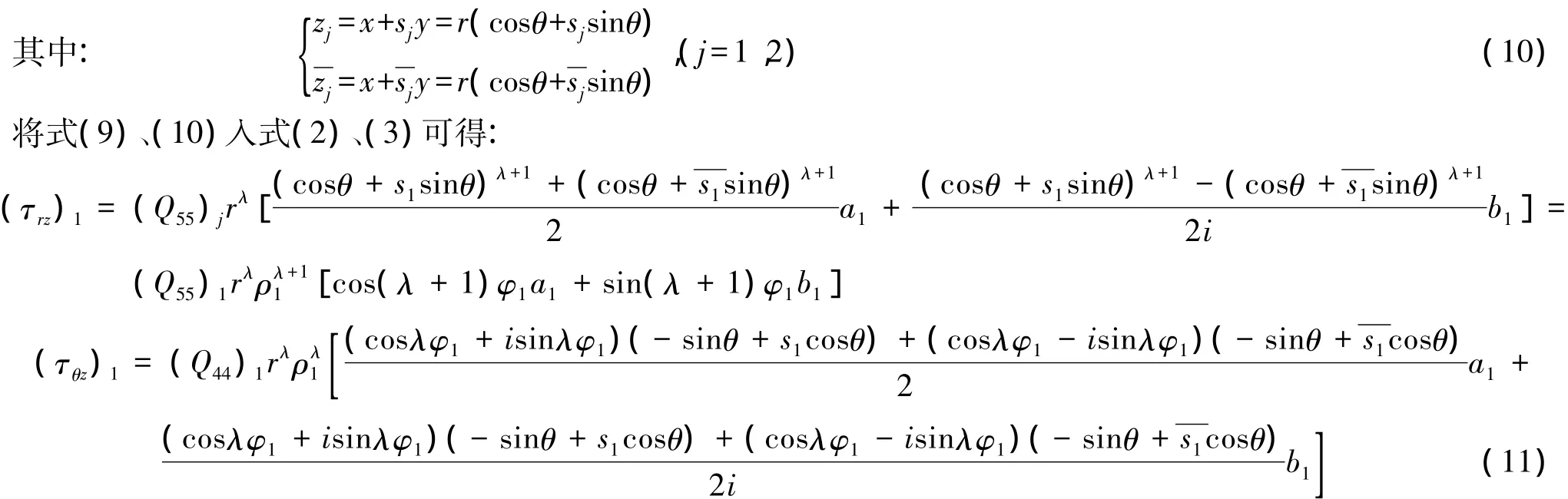
同理可得出(τrz)2，(τθz)2.

将式(11)代入 式(4)～(6)可得到一组关于(a1，a2，b1，b2)的四阶齐次线性方程组:

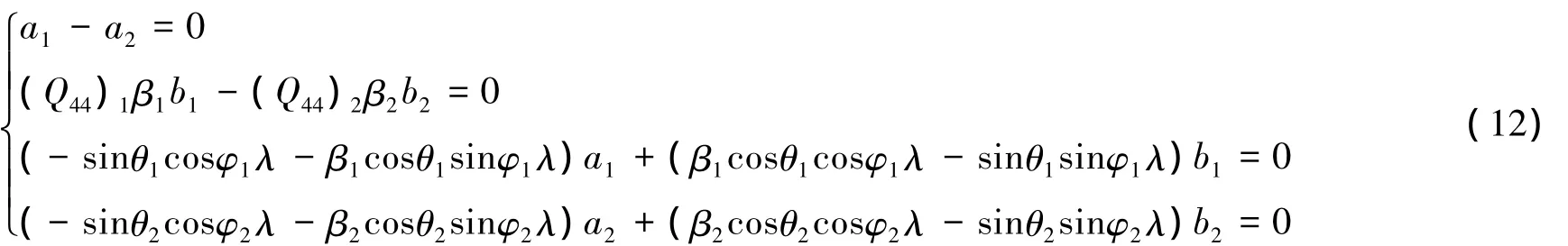
由式(12)得:a1=a2，(Q44)1β1b1=(Q44)2β2b2.

式(12)是一组齐次线性方程组，要使式(12)有一组非零解，则由线性方程组定理知，其系数的行列式必为零.因此可求解出关于λ的特征方程:

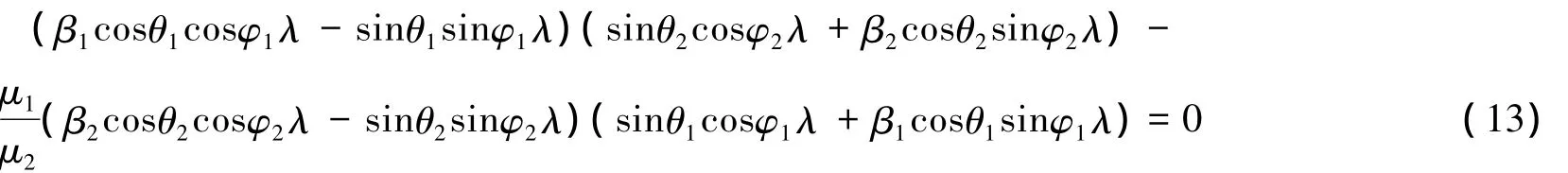
其中:μj=βj(Q44)j(j=1，2)

一般情况下，方程(13)根有很多，有可能是实数，也有可能是复数.考察式(13)不难看出，当给出的复合材料组合确定时，就可以试图通过改变角度θ1，θ2的值，找到使其界面端附近应力场奇异消失的根，下面来研究两种特殊非对称界面端的应力奇异性的相关问题.

4 两种特殊反平面非对称界面端的应力奇异性

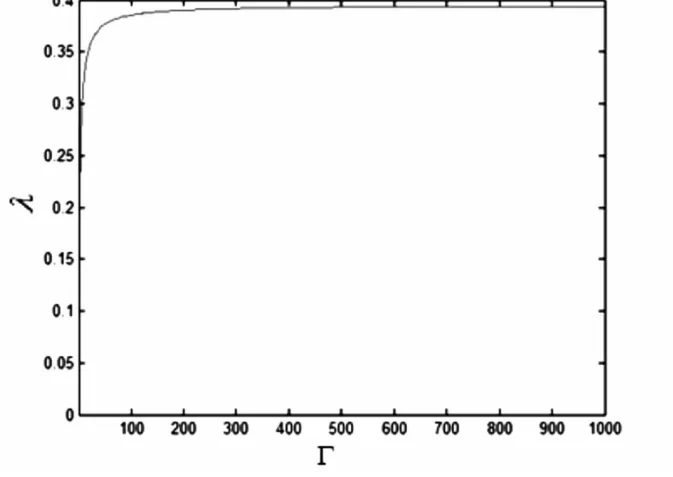
图2 特征根λ随材料参数Γ的变换图F i g.2 The transformation graph of λ eigenvalue changing with material parameter Γ

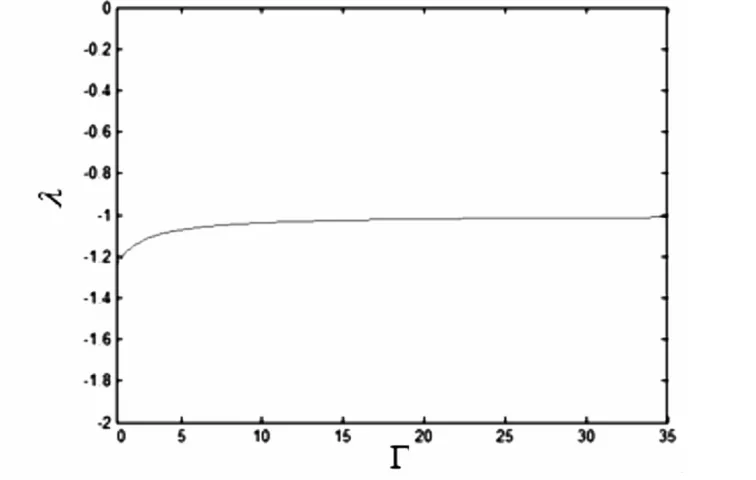
图3 特征根λ随材料参数Γ的变换图Fig.3 The transformation graph of λ eigenvalue changing with material parameter Γ

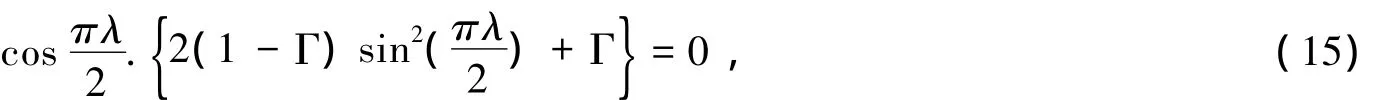
当Γ≤2时，可得λ=±1，3，5，…在这种情况下，双材料(正交异性)反平面界面端附近的应力场是不存在奇异性的.

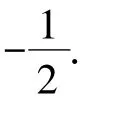
5 结论

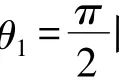
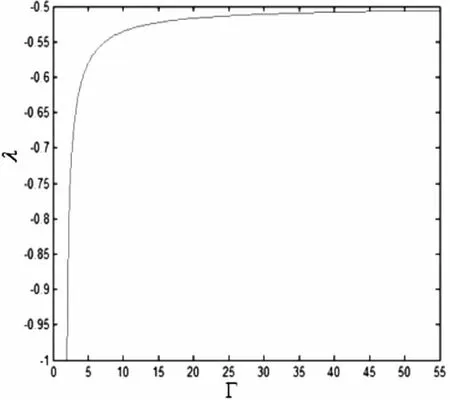
图4 λ随Γ变换图Fig.4 The transformation graph of λ changing with Γ

［1］李俊林，王小丽.正交异性双材料反平面界面端应力场分析［J］.应用数学和力学，2009，9:1078－1084.

［2］程靳，宋兆滨，翟云喜.正交异性体弹性动力学的一类反平面问题［J］.哈尔滨工业大学学报，1994，26(3):140－147.

［3］王小丽，李俊林，杨雅娟，等.双材料反平面对称界面端的应力奇异性研究［J］.太原科技大学学报，2010，31(3):222－225.

［4］Zhang Shaoqin，Yao Hesheng，Li Junlin.Stress Fields near Mode II Interface Crack Tip of Two Dissimilar Orthotropic Composite Materials［J］.Key Engineering Materials Vols，2008，385/387:585－588.

［5］Li Junlin，Zhang Shaoqin，Yang Weiyang.Stress Field near Interface Crack Tip of Double Dissimilar Orthotropic Composite Materials［J］.Applied Mathematics and Mechanics，2008，29(8):1045－1052.

［6］许金泉，姜菊生.界面端附近裂纹的应力强度因子［J］.上海力学，1998，19(3):221－227.

［7］董安强，李俊林.正交异性双材料反平面界面端应力奇异性研究［J］.科学技术与工程，2012，12(3):638－641.

［8］杨维阳，李俊林，张雪霞.复合材料断裂复变方法［M］.北京:科学出版社，2005.