基于AHP－GA的地质旅游资源评价研究

丁圆婷，于吉涛*，宋鄂平

(1.河南理工大学测绘与国土信息工程学院，河南焦作 454000;2.湖北民族学院生物科学与技术学院，湖北恩施 445000)

2000年9月，国土资源部下发《关于申报国家地质公园的通知》(国土资厅发［2000］77号)，正式拉开我国申报、建设国家地质公园的大幕.2001年3月经国家地质遗迹(地质公园)评审委员会评审和国家地质公园领导小组批准，正式公布了首批11处国家地质公园名单.经过10余年的发展，截止2013年底我国大陆已分6批正式批准建立了201家国家地质公园，分9批有29家国家地质公园(包括中国香港)入选联合国教科文组织支持的世界地质公园网络名录.伴随着地质公园这一事物的诞生，国内很多的研究人员从不同方面入手对地质公园或地质遗迹开展了相关研究工作，这些研究工作归纳起来主要包括地质公园的基础理论研究、地质公园与旅游、地质公园保护与管理、地质公园与区域经济发展等方面.在这些研究工作中，有关地质公园(地质遗迹)定量评价工作是“贯穿地质公园申报→地质公园建设→地质旅游资源开发”这一过程中最核心的内容.

在地质公园申报阶段，申报单位依据国土资源部77号文件有关国家地质公园评审标准，基于地质公园的自然属性、可保护属性和保护管理基础三个方面对国家地质公园定量赋分，更加关注地质遗迹资源本身的典型性、稀有性、自然性、系统性和完整性、优美性等方面［1］.另外，很多机构在对地质遗迹景观综合价值等级评价时，常参考国家旅游局颁布的《旅游资源分类、调查与评价GB T18972—2003》中有关“景观质量评分细则”［2］，结合《中国国家地质公园建设技术要求和工作指南》中的地质景观评价指标［3］，制定出既考虑了地质遗迹景观本身的价值又考虑其它条件价值的综合定量评分体系.这两种方法可满足地质公园申报阶段的评价工作所需，但是往往得到的不同园区(或景区)的评价结果相差不大，并且更大程度上基于不同判别人士的主观认识.因此，国内学术界对地质遗迹资源评价多在定性评价(经验的)的基础上采用数学模型(定量的)进行评价，即综合性评价方法.常用的主要方法有层次分析法、综合价值评价法、模糊赋分法、特尔菲法等［4］.其中，由美国著名的运筹学家、匹兹堡大学教授Saaty于20世纪70年代初提出的层次分析法(Analytic Hierarchy Process，AHP)，作为一种定性和定量相结合的多目标决策方法［5］，在地质遗迹评价中应用较为广泛［6－11］.但常规层次分析法通常采用专家打分、多轮意见征询等方法修改调整判断矩阵，耗时、费力、工作量大，且效果也不一定理想.基于此，本文通过构建国家地质公园旅游开发决策系统，尝试采用AHP法和AHP－GA法进行决策评价、对比，以期为地质旅游资源开发带动型县域经济发展模式的地区提供更具针对性的决策依据.

1 层次分析法与遗传算法

1.1 层次分析法的步骤

1)基于目标建立层次结构模型.针对复杂的决策系统，从利于决策的角度出发，将系统进行递价分层，依次划分为目标层、准则层(可为多层)和方案层，每一层可包含多个指标(准则C1～Cn，U1～Um或方案P1～Pi，n，m，i=1，2，…，n)，构建一个各指标相互联结的层次结构模型，如图1所示.

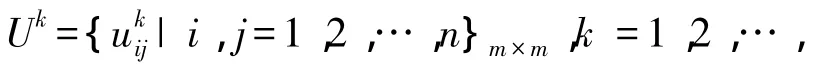
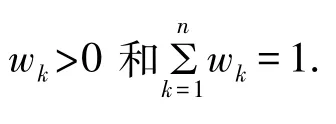
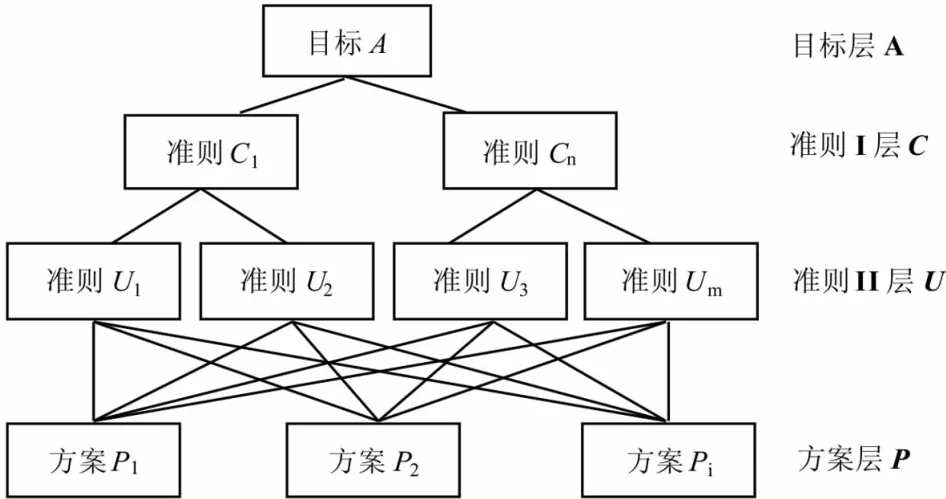
图1 基于目标建立的层次结构模型Fig.1 The hierarchical structure model based on the target

由公式(1)可知，如果计算出的CI值为零，那么判断矩阵满足完全一致性条件，则满足cij=wi/wj(i，j=1，2，…，n).但实际情况是，当人们对客观问题进行评估时，由于每个人对问题的主观认识有所偏差，很难达到完全一致性，因此处于应用的考虑，采用了人为设定的满意一致性(CI＜0.10).判断矩阵C的一致性程度主要取决于判断人员对决策系统各指标的掌握程度，掌握程度越深入，矩阵的一致性程度就越高.层次分析法在应用过程中存在的主要问题就是判断矩阵的一致性问题，这也是目前层次分析法研究的难点和热点.

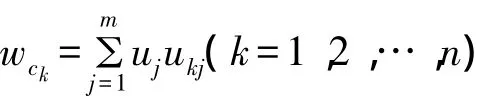
同样只有当CR＜0.10，才认为这一层的总排序结果满足满意一致性检验，而当CR大于0.10时，就需要对判断矩阵的元素取值进行重新调整.

1.2 遗传算法

由层次分析法的计算步骤可以看出，层次分析法拟解决的核心问题是步骤3)采用何种方法来计算判断矩阵的特征根和特征向量.常用的计算方法除了最简单的和积法和方根法之外，应用较多的还有［12－14］:行和正规化法、列和求逆法、特征值法、梯度特征值法、对数回归法、最小平方法和最小偏差法等.这些方法致力解决的关键问题是如何合理计算判断矩阵的排序权值，但是归根到底本质问题是如何解决判断矩阵的一致性问题.由上文步骤3):如果判断矩阵C={cij|i，j=1，2，…，n}n×n，满足完全一致性条件，所计算的各指标的单排序的权值{wk|k=1，2，…，n}，那么 cij=wi/wj(i，j=1，2，…，n)，于是就有:

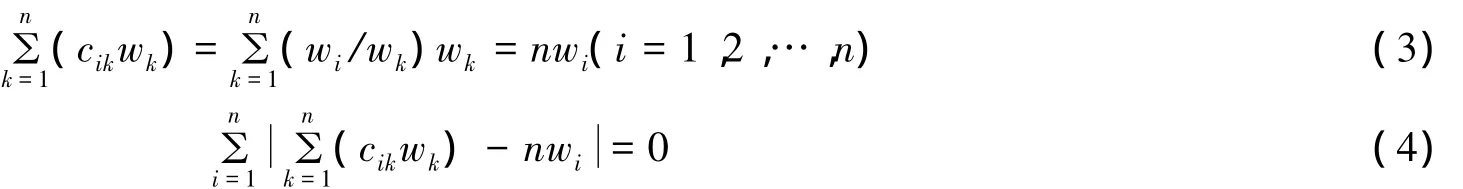
金菊良等将式(4)左端变换后标记为CIF(n)，称为一致性指标函数［15］(consistent index function).如果CIF值越趋近于0，则判断矩阵C的一致性程度就越高.这就将层次分析法中的判断矩阵的排序权值的计算和一致性检验问题转化为针对特定目标、决策的非线性优化问题，这一问题采用常规方法较难处理.如下式(5)所示.

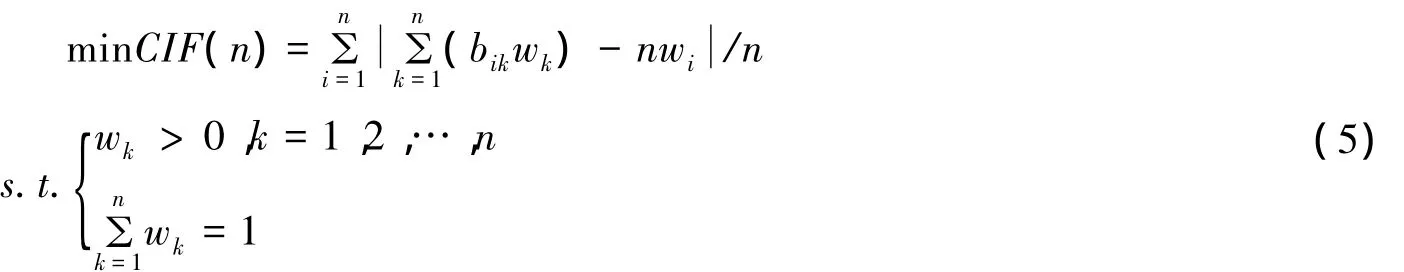
基于模拟生物优胜劣汰规则与群体内部染色体信息交换机制的遗传算法(genetic algorithm，简称GA)，是一种全局寻优的优化算法，用GA来求解公式(5)十分简便、有效.采用遗传算法对层次分析法的指标权重进行优化已引起广泛关注［16－18］，主要采用的算法是标准遗传算法(SGA)和加速遗传算法(AGA).但这些算法在地质遗迹、地质旅游资源评价方面尚没有明显应用.

2 基于AHP－GA的思南乌江喀斯特国家地质公园旅游资源开发评价

贵州思南乌江喀斯特地质公园位于黔东北铜仁地区西部思南县境内，公园占地面积202.99 km2，主要地质遗迹面积 35.94 km2(其中一级保护区面积 23.41 km2).地理坐标:107°52'～108°28'E，27°32'～ 28°09'N.公园以喀斯特地貌景观为主体，结合峡谷地貌、水体景观、生态景观与人文景观，集地学资源的独特性、系统性、科学性与观赏性于一身的大型喀斯特地貌型地质公园.公园分别由长坝、文家店－荆竹园、思林、青杠坡、鹦鹉溪、板桥、思唐等七个景区组成.作为原先的国家级贫困县，确定地质公园带动县域经济的发展模式，就需要平衡地方经济发展与地质遗迹保护之间的关系，也需要确定县域地质旅游景观开发顺序这一关键问题，这就需要在国家地质公园的开发和建设过程中制定科学的旅游开发决策.

2.1 基于AHP法评价

2.1.1 选取评价因子 评价因子的选取是进行国家地质公园旅游开发决策评价的基础和关键，这些评价因子既要针对地质遗迹资源自身的自然属性，也要考虑这些地质遗迹资源的科学、美学及科普价值，还要体现可持续发展的理念，即体现“在保护中开发，在开发中保护”的原则;同时作为一种待开发的旅游资源，也需要分析公园及所在区域的开发条件.曾文煜根据旅游资源的评价体系，选取自然属性、价值属性、保护条件、景观特征和开发条件等5个评价指标和20个评价因子，采用层次分析法对陕西商南金丝峡国家地质公园和陕西岚皋南宫山国家地质公园进行了决策评价［8］.这一评价模型一方面体现了国土资源部地质环境司关于国家地质公园评审时所依据的指标体系，另一方面也较好的体现了地质公园自身以及公园内涵盖的地质遗迹各个方面的因素，因此本文也倾向采用这一评价体系(如表1).但是，本文是针对一个公园各个景区进行量化计算，通过将各个景区作为层次分析模型的方案层，自上而下分别采用AHP法和AHP－GA法进行决策评价，并且将两种方法的决策结果进行对比分析，一方面可进一步对思南县地质旅游的开展进行更准确的决策，另一方面也希望能较好地解决运用层次分析法时可能出现的人的主观因素偏差所致的层次一致性难以保证的问题.

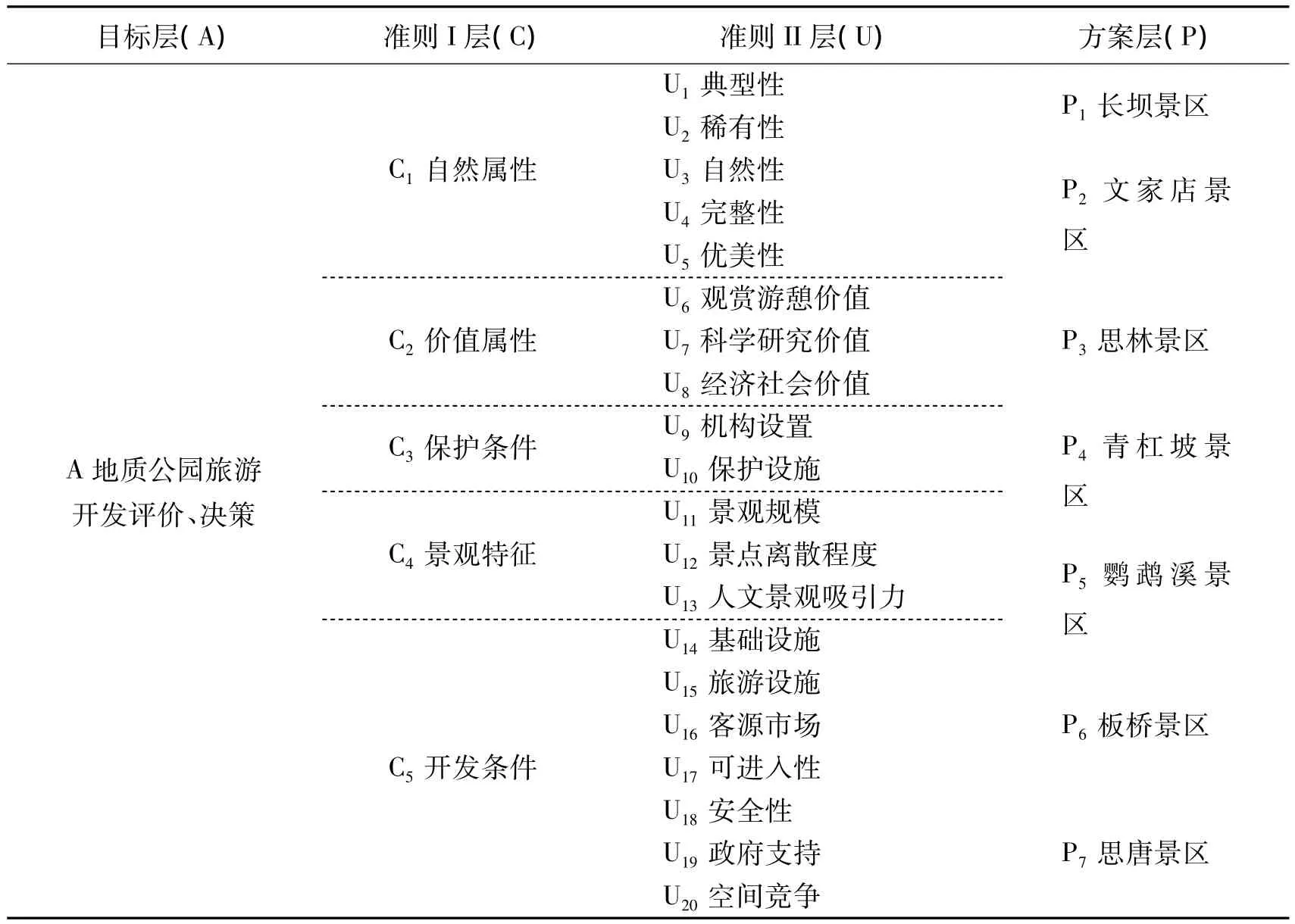
表1 贵州思南乌江喀斯特国家地质公园地质旅游评价决策系统Tab.1 The geological tourism evaluation and decision system of Wujiang Karst National Geopark，Sinan，Guizhou

2.1.2 建立评价体系 思南乌江喀斯特国家地质公园地质旅游评价、决策模型如表1所示，目标层为A，目标是对思南乌江喀斯特国家地质公园的地质旅游资源进行评价、决策;准则I层为C层，包括针对地质遗迹资源的自然属性、价值属性及地质公园自身开发的保护条件、景观在公园内的分布特征、公园自身的开发条件等;准则II层为U层，是指针对准则I层C层各个指标所涵盖不同的评价内容(评价因子);方案层为P层，是指公园的长坝景区、文家店－荆竹园景区、思林景区、青杠坡景区、鹦鹉溪景区、板桥景区和思唐景区，共七个景区.

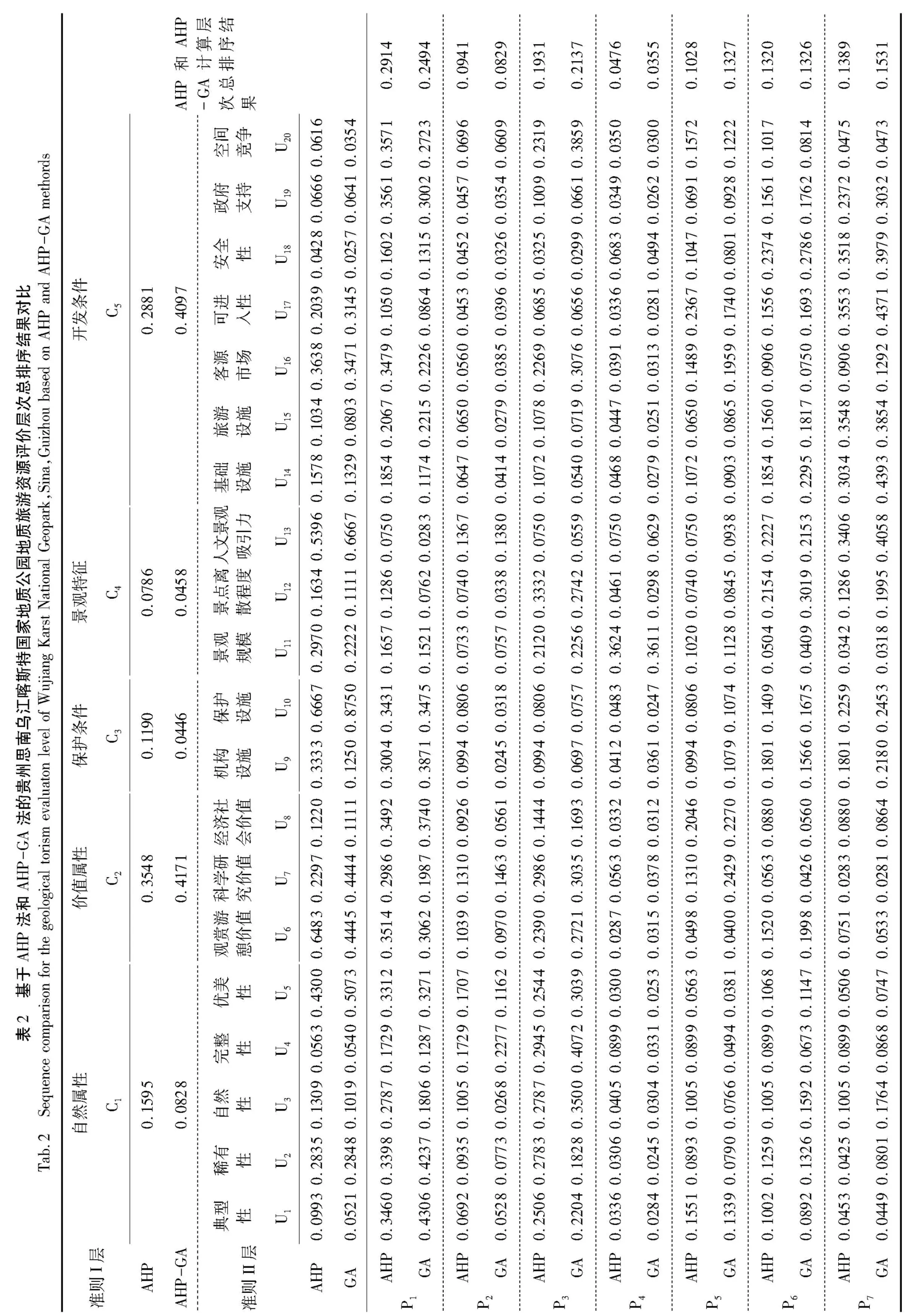
2.1.3 AHP计算 按照层次分析法的计算步骤2)～4)，构建目标层－准则I层判断矩阵A－C矩阵1个，构建准则I层－准则II层判断矩阵C－U矩阵5个，构建准则II层－方案层判断矩阵U－P矩阵20个，计算各个矩阵的权重并通过一致性检验，根据公式(2)对C－U层、U－P层进行层次总排序一致性检验:C－U层:CI=0.0461，RI=0.8103，CR=0.0569＜0.10，满足一致性检验;U－P 层:CI=0.1548，RI=6.6000，CR=0.023 5＜0.10，满足一致性检验.最终经AHP法计算的贵州思南乌江喀斯特国家地质公园地质旅游评价、决策的层次排序结果如表2所示.

2.2 基于AHP－GA评价

采用标准遗传算法(SGA)，选取种群大小为40，染色体长度为52，最大进化代数为25，代沟为0.9，以公式(5)作为目标函数，通过调整矩阵的标度范围而对层次结构模型进行优化，得到的C－U层、C－U层层次总排序一致性检验结果为:C－U 层:CI=0.021 4，RI=0.773 9，CR=0.027 7＜0.10;U－P层:CI=0.069 9，RI=6.6000，CR=0.0106＜0.10.

计算结果比基于层次分析法所得到的一致性检验结果更优.基于AHP－SGA法所计算出的贵州思南乌江喀斯特国家地质公园地质旅游评价、决策的层次排序结果如表2所示.

2.3 评价结果与讨论

1)对七个景区基于AHP法得到的最终排序顺序为:P1长坝景区(0.2914)＞P3思林景区(0.1931)＞P7思唐景区(0.1389)＞P6板桥景区(0.1320)＞P5鹦鹉溪景区(0.1028)＞P2文家店景区(0.0941)＞P4青杠坡景区(0.0476);基于AHP－GA法得到的最终排序顺序为:P1长坝景区(0.2494)＞P3思林景区(0.2137)＞P7思唐景区(0.1531)＞P5鹦鹉溪景区(0.1327)＞P6板桥景区(0.1326)＞P2文家店景区(0.0829)＞P4青杠坡景区(0.0355).两种方法得到的排序结果稍有不同(如图2)，长坝景区的“思南石林”类型丰富、形态多样，在全国范围内具有较高的对比意义，是该公园最核心的景区;思林景区峡谷－喀斯特瀑－天生桥－地下峡谷－盲谷－溶洞的组合在成因上与乌江河谷的下切密切相关，在喀斯特学研究与科普上具有重要现实意义，是仅次于长坝景区的另一核心景区.基于AHP－GA法压低了长坝景区的得分权重，而一定程度提高了思林景区的权重值，更加能够体现这两大核心景区的地位.

另外，思唐景区的江心洲－边滩－民俗－思南古建筑群组合，蕴涵了浓厚的民族风情，体现了多民族文化融合、多宗教交汇，是该公园的重要景区.而两种方法排序顺序不同的是鹦鹉溪景区和板桥景区，从目前实际情况看，以温泉－冷泉－溶洞组合为主的鹦鹉溪景区，因贵州省内水温最高的天然泉水——罗湾坨热泉的发现，相比于以峰丛—喀斯特泉—明清古民居群－溶蚀洼地组合为主的板桥景区，应更具有开发潜力，AHP－GA法得到的评价结果更能体现出这一点.而文家店景区和青杠坡景区相比来讲，开发潜力较差.

2)由表2也可以看出，由AHP方法和AHP－GA方法所计算的每一层指标的权重结果有所不同，但是两种方法对层次评价模型中各指标权重所能指示的意义基本相同.如决定公园地质旅游景观的5个大的指标—自然属性、价值属性、保护条件、景观特征、开发条件，相对而言价值属性和开发条件更加重要，不同之处在于基于AHP－GA法得到的计算结果更加凸显了价值属性和开发条件这两个因素的重要性.而公园自然属性方面，AHP－GA法也更加凸显了优美性的重要性;价值属性方面，也都能指示景观的观赏游憩价值和科学研究价值更为重要，但AHP－GA法体现了地质公园的观赏游憩价值和科学价值同等重要;保护条件方面，两种方法都指出保护设施比机构设施更为重要;景观特征方面，两种方法也都指出人文景观吸引力更为重要;开发条件方面，两种方法皆指示了客源市场和可进入性这两个指标更为重要，但AHP－GA法指示了客源市场与可进入性几乎同等重要.综上所述，基于AHP－GA法得到的思南乌江喀斯特国家地质公园各个景区最终权重值的排序结果更加科学，这对于思南县基于地质旅游资源开发带动县域经济发展的开发、决策更有针对性和指导意义.

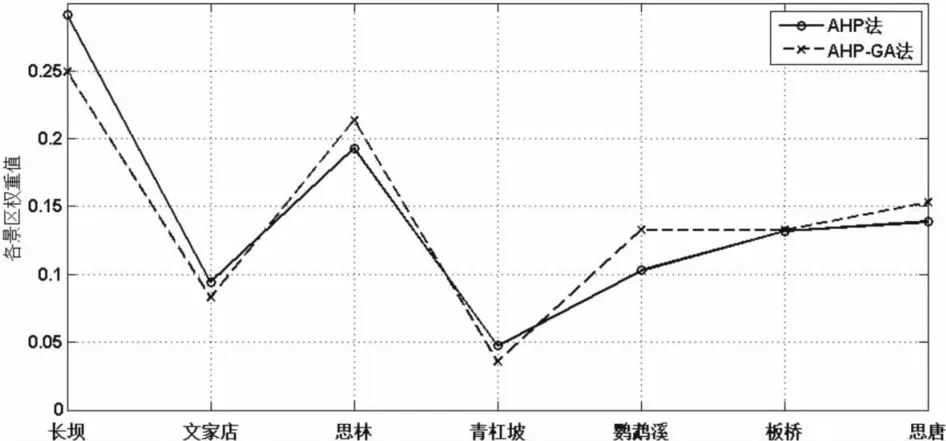
图2 AHP法和AHP－GA法得到的方案层最终权重对比Fig.2 The final weight comparison of the solution layer based on the method of AHP and AHP－GA

3 结论

目前在旅游资源评价方面，AHP方法由于其高度的逻辑性、系统性的特点，以及针对系统目标处理灵活简洁的优点，被广泛使用.但AHP法存在着人的主观因素影响较大，构建的判断矩阵一致性检验难以通过的问题.本文采用遗传算法优化AHP法构建的各个判断矩阵，并基于AHP－GA法对思南乌江喀斯特国家地质公园七个景区的开发、决策顺序进行了量化评价，两种方法所计算出来的结果进行对比，得出如下结论:

1)AHP－GA法能较好地解决常规层次分析法由于可能出现的人的主观因素偏差所致的层次一致性难以保证的问题，计算结果比常规层次分析法更优，这一方法目前在地质遗迹评价、地质旅游资源开发方面应用较少.

2)构建贵州思南乌江喀斯特国家地质公园旅游开发评价、决策系统，采用AHP－GA法对地质公园所覆盖的7个景区进行定量评价，最终评价结果按权重高低依次为长坝景区、思林景区、思唐景区、鹦鹉溪景区、板桥景区、文家店景区、青杠坡景区，评价结果将对思南县基于地质旅游资源开发带动县域经济发展的地区提供更具针对性的决策依据.

［1］国土资源部.关于申报国家地质公园的通知(国土资厅发［2000］77号)［A］.2000－09－22.

［2］GB/T18972－2003.旅游资源分类、调查与评价［S］.2003.

［3］国土资源部地质环境司.中国国家地质公园建设工作指南［M］.北京:中国地大出版社，2006.4.

［4］黄喜峰，庞桂珍，杨望暾，等.陕西金丝峡地质公园旅游资源及综合评价［J］.生态经济，2010(1):102－103，109.

［5］Satty T L.The analytic hierarchy process［M］.New York:Mcgraw－Hill，1980.

［6］方世明，李江风，赵来时.地质遗迹资源评价指标体系［J］.地球科学－中国地质大学学报，2008，33(2):285－288.

［7］张国庆，田明中，刘斯文，等.地质遗迹资源调查以及评价方法［J］.山地学报，2009，2009，27(3):361－366.

［8］曾文煜.基于层次分析法的国家地质公园旅游开发决策研究［D］.长安大学，2010.

［9］王艳红，武法东.综合定量评价方法在内蒙古巴彦淖尔地质公园地质遗迹资源评价中的运用［J］.中国农学通报，2013，29(4):210－215.

［10］齐文涛，吴天伟，木合塔尔·扎日，等.新疆富蕴县五彩湾地质遗迹景观资源评价［J］.干旱区资源与环境，2013，27(4):160－164.

［11］肖景义，侯光良，唐仲霞，等.青海省贵德国家地质公园地质遗迹及综合评价［J］.地球学报，2013，34(1):111－120.

［12］王莲芬.层次分析法中排序权数的计算方法［J］.系统工程理论与实践，1987(2):31－37.

［13］王莲芬.梯度特征向量排序法的推导与改进［J］.系统工程理论与实践，1989(2):17－21.

［14］徐泽水.层次分析中判断矩阵排序的新方法—广义最小平方法［J］.系统工程理论与实践，1998(9):38－43.

［15］金菊良，魏一鸣，付强，等.层次分析法在水环境系统工程中的应用［J］.水科学进展，2002，13(4):467－472.

［16］黄燕玲，罗盛锋，程道品.基于GA优化的农业旅游地可持续发展能力评价—以西南少数民族地区为例［J］.旅游学刊，2009，24(10):32－37.

［17］金菊良，张礼兵，张少文，等.层次分析法在水资源工程环境影响评价中的应用［J］.系统工程理论方法应用，2004，13(2):187－192.

［18］丁琨，张薇薇，金菊良，等.改进层次分析法在引水工程方案优选中的应用［J］.人民黄河，2010，32(6):86－88.