具有小周期震荡参数时间分数阶扩散方程的二阶双尺度有限元算法

王自强，曹俊英

(贵州民族大学理学院，贵州贵阳 550025)

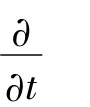
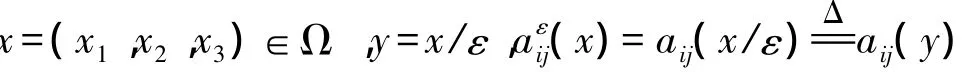
1 二阶双尺度渐近展开式的构造及逼近性分析

考虑问题:

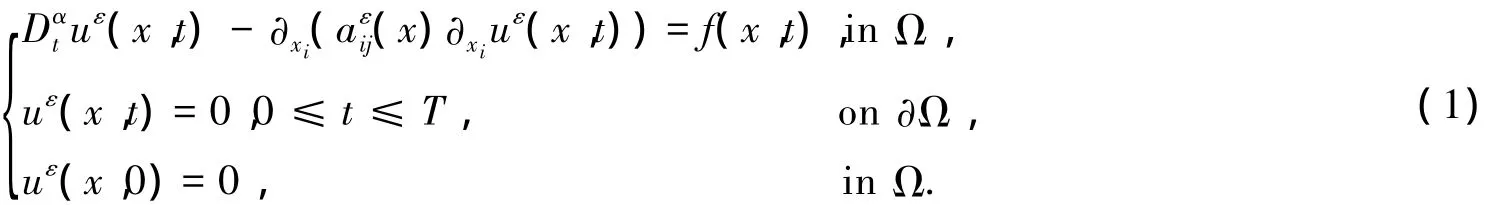
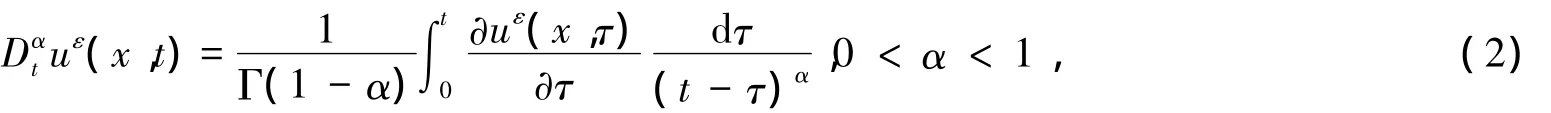
类似于文献［1，7－8］，假设(1)的解具有下面的多尺度渐近展开式:

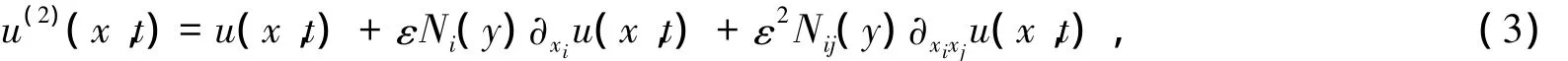
这里:

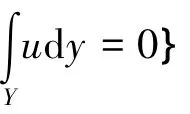
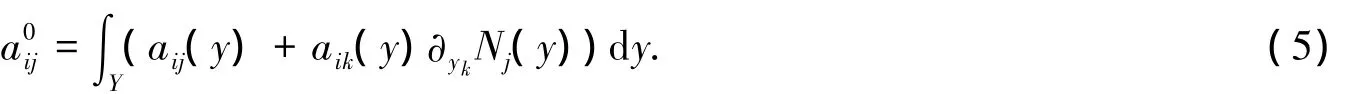
iii)均匀化方程为:

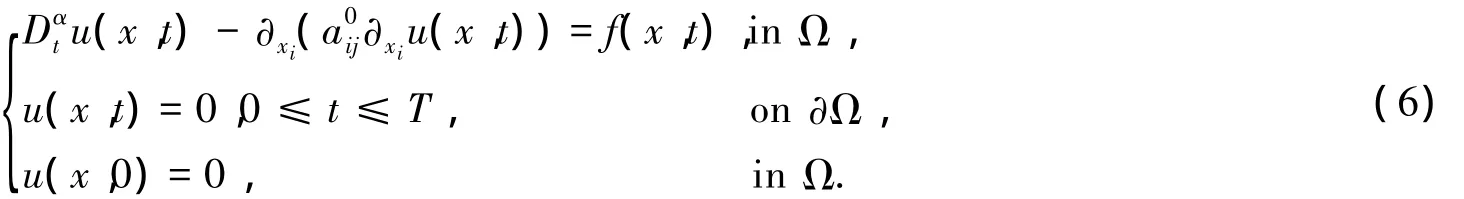
iv)局部函数Nij(y)属于V且满足:

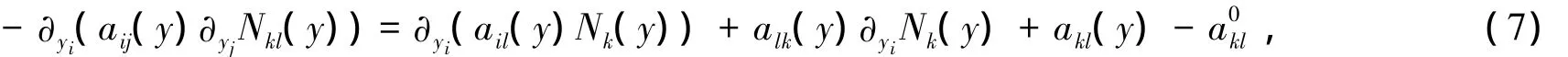
利用文献［1］中处理热传导方程二阶双尺度渐近展开式的收敛性分析方法和文献［6］分析时间分数阶方程解始定性的技巧，可以证明下面的结果:

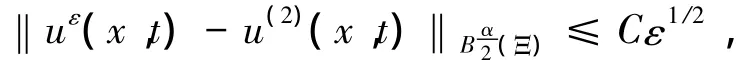
2 基于二阶双尺度渐近展开式的有限元算法及数值算例

类似于文献［7］，建立问题(1)的二阶双尺度有限元算法如下:

3)在参考单胞Y上利用与(ii)相同的有限元网格求解方程(7)得到二阶的局部函数(y)的近似值.

为了验证本文提出算法的有效性，下面对问题(1)进行二阶双尺度近似解的计算.取f=10，α=0.6，ε=0.1，T=1，Ω=［0，1］2和 Y=［0，1］2.进一步，设方程(1)的系数为在 Y1中 aij(y)= δij和在 Y1中 aij(y)=0.01δij.在图3～6中分别给出了uε的细网格有限元解，均匀化解u，一阶双尺度近似解u(1)和二阶双尺度近似解u(2).

图1 宏观区域ΩFig.1 The macro domain Ω

图2 参考单胞YFig.2 The reference cell Y

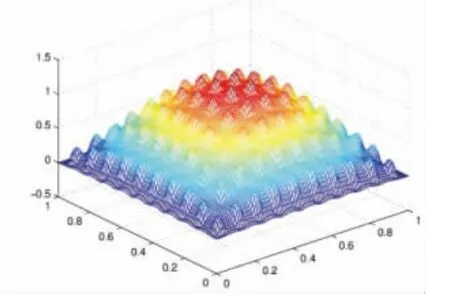
图3 uε的细网格有限元解Fig.3 The FEM solution of uεin refined mesh

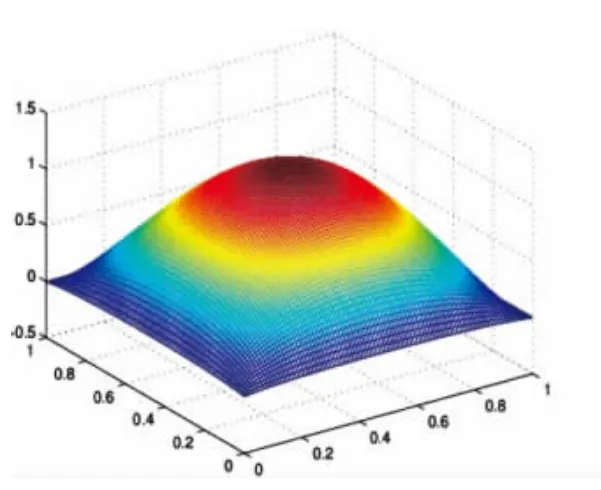
图4 均匀化解uFig.4 Homogenization solution u

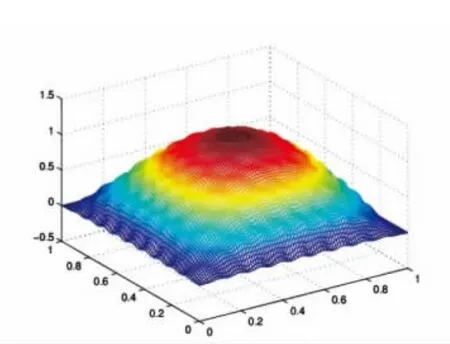
图5一阶近似解u(1)Fig.5 FOTS’s solution u(1)

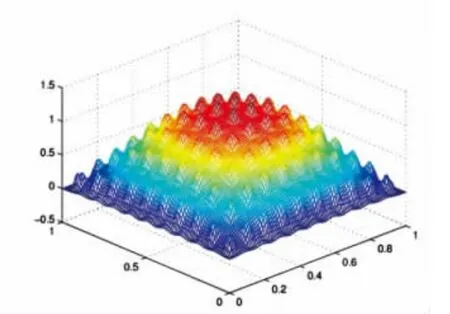
图6 二阶近似解u(2)Fig.6 SOTS’s solution u(2)

通过图3～6可知:均匀化解u仅仅可以反映出uε变化的宏观特征，一阶双尺度近似解u(1)可以反映出uε的部分特征，二阶双尺度近似解u(2)是比一阶双尺度近似解u(1)对uε的一个更好的近似.

［1］王自强，尹文双，张恩宾.平面复合材料热传导问题的一个新的多尺度渐近展开式［J］.湖北民族学院学报:自然科学版，2008，26(4):391－394.

［2］Bagley R L，Calico R A.Fractional order state equations for the control of viscoelastically damped structures［J］.Journal of Guidance，Control，and Dynamics，1991，14(2):304－311.

［3］Benson D A，Wheatcraft S W，and M M.Meerschaert.Application of a fractional advection dispersion equation［J］.Water Resour Res，2000，36(6):1403－1412.

［4］Cao J Y，Xu C J，Wang Z Q.A high order finite difference/spectrial approximations to the time fractional diffusion equations［J］.Advanced Materials Research，2014，875－877:781－785.

［5］Lin Y M，Xu C J.Finite difference/spectral approximations for the time－fractional diffusion equation［J］.J Comput Phys，2007，225(2):1533－1552.

［6］Li X J，Xu C J.A space－time spectral method for the time fractional diffusion equation［J］.Siam J Numer Anal，2009，47(3):2108－2131.

［7］Cui J Z，Yang H Y.A dual coupled method for boundary value problems of PDE with coefficients of small periodic［J］.J Comput Math，1996，14:159－174.

［8］Wang Z Q，Cao J Y.Second Order Two－scale Method for Composite Plate with 3－D Periodic Configuration under Condition of Coupled Thermoelasticity［J］.Advanced Materials Research，2014，898:7－10.