统计收敛意义下的Slutsky定理

张 宾

(湖北民族学院预科教育学院，湖北恩施 445000)

0 引言

在文献［1－2］利用自然密度的概念将实数序列的极限推广得到了实数序列的统计收敛的概念，文献［3］讨论了随机变量的统计收敛性，分别定义了统计几乎必然收敛性、统计依概率收敛性和统计依分布收敛性，文献［4－7］研究了统计收敛的测度理论.Slutsky定理经常用来寻求一些统计量的渐近分布，近些年来，有学者对Slutsky定理进行了推广文献［8－9］，本文考虑了统计收敛意义下的Slutsky定理，证明了在统计收敛意义下Slutsky定理仍然成立.

下面给出文献［3］中的两个定义:

定义1称 xn{ }统计依概率收敛于X，如果对任意的ε＞0，有:

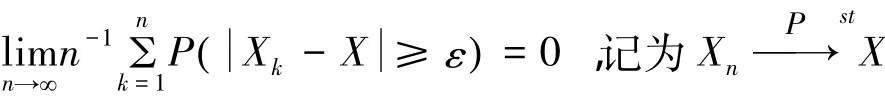
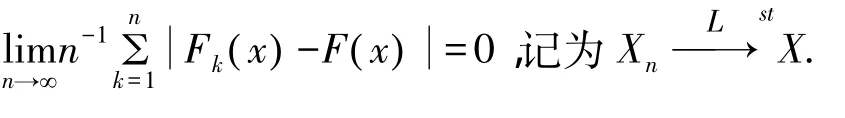
1 主要结论

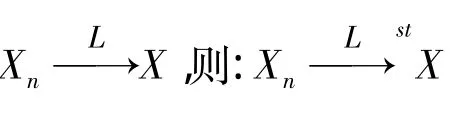
例1记N表示服从标准正态分布N( 0 ，1)的随机变量，设:

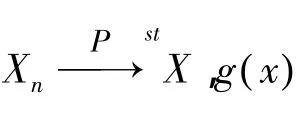
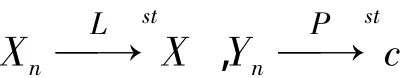
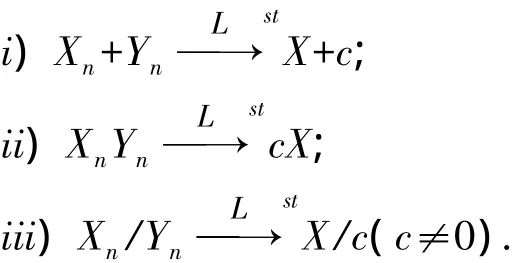
2 主要结论的证明

定理1的证明:

i)设随机变量X的分布函数为F x()，则X+c的分布函数为F x－c( )，根据定义2，即需证明对F x－c( )的连续点x－c，成立:

类似(i)中式(1)可得，∀ε＞0，有:

iii)证明和ii)类似，不再赘述.

［1］Fast H.Sur la convergence statistique［J］.Colloq Math 2，1951(2):241－244.

［2］Fridy J A.Statistical limit points［J］.Proc Amer Math Soc，1993，118(6):1187－1192.

［3］刘君霞，刘卫东，林正炎，等.随机变量的统计收敛性［J］.浙江大学学报:理学版，2007，34(2):132－135.

［4］蓝永艺.统计收敛与概率测度［J］.数学研究，2006，39(4):441－446.

［5］程立新，蓝永艺，林国琛，等.统计收敛的测度理论［J］.中国科学A辑:数学，2008，38(4):450－468.

［6］蓝永艺.统计收敛与平均收敛［J］.集美大学学报:自然科学版，2010，15(2):147－149.

［7］蓝永艺，邹增堂.随机变量的依概率统计收敛［J］.西南师范大学学报:自然科学版，2012，37(11):10－13.

［8］李国亮.Slutsky定理的一个推广［J］.数学杂志，2003，23(2):166－168.

［9］陈菲，宋立新.关于Slutsky定理的推广［J］.吉林师范大学学报:自然科学版，2005(2):41－44.