热力学关系式的关联记忆＊

塔金星

（东北林业大学理学院 黑龙江 哈尔滨 150040）

1 引言

在学习热力学统计物理这门课程时，有许多热力学关系式需要牢记，但是学生们学不得法，找不到这些公式的内在联系，只是孤立片面地学习，给应用这些公式求解问题带来很大的障碍.因此，在教学过程中如何使学生们牢记三者之间的关系式就显得十分重要.

本文将从3个基本热力学函数内能、物态方程、熵出发，采用联想法将热力学关系式建立联系来记忆，最后给出应用关系式的例子.

2 联想法记忆热力学关系式

2.1 内能主线

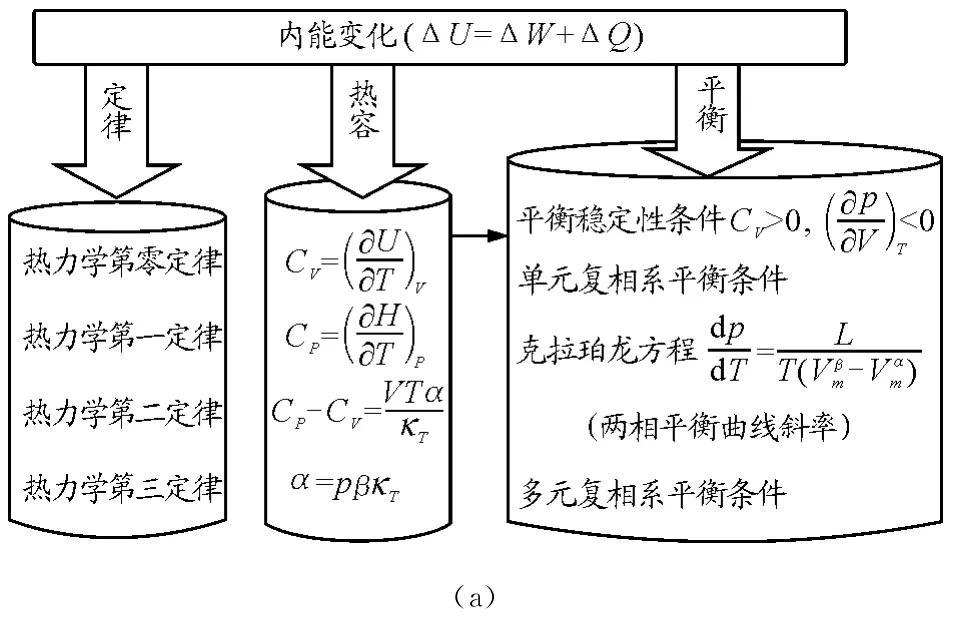
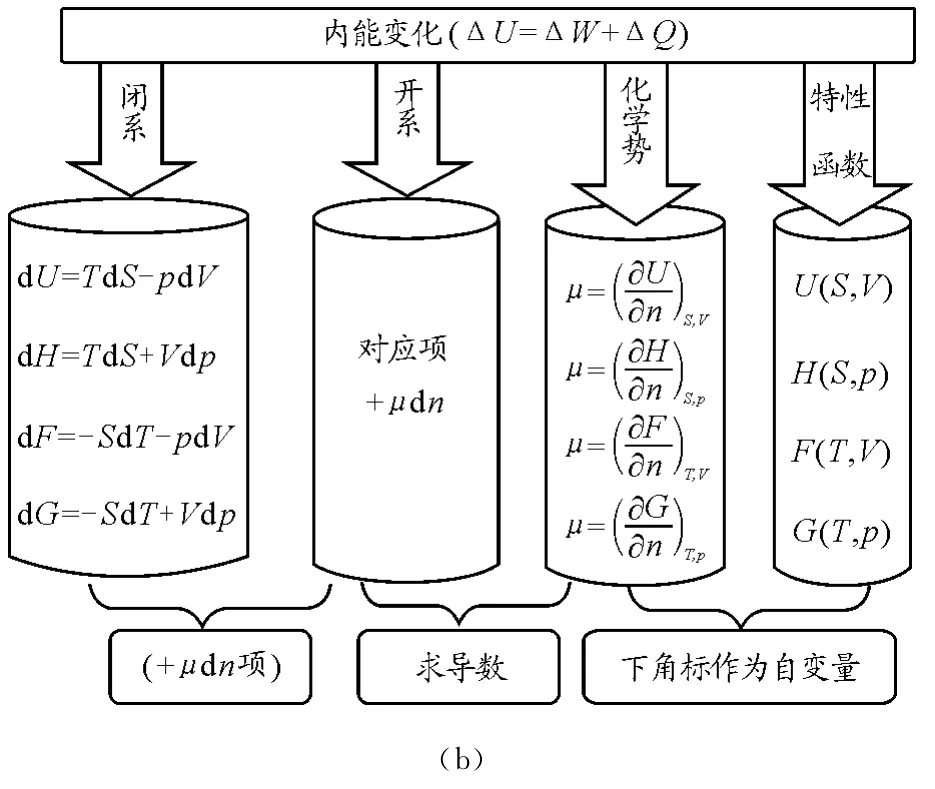
图1 以内能为主线联想记忆脉络图

如图1（a）所示，以内能为主线，由内能变化衍生出关键词：定律、热容、平衡内能变化对应热力学第一定律（ΔU＝ΔW＋ΔQ），由此联想到其他3个定律，从而掌握它们的各种表述及实质；还可以联想到热容，包括等容和等压热容及其二者之差的公式，由公式中的体胀系数联想到和压强系数和等温压缩系数的关系式；由热容的符号问题可以联想到平衡稳定条件，从而扩展到单、多元复相系的平衡条件以及两相平衡曲线斜率的克拉珀龙方程.其他细节问题留给学生补充.

图1（b）给出了由内能变化联想到的一些热力学关系式.首先是基本热力学方程由此可以想到其他3个关系式.对应项＋μdn项即为开系的热力学方程.对这4个等式求导数，则可用内能、焓、自由能、吉布斯函数导数表示出化学势μ，并可以联想到把下角标作对应函数的自变量后便是特性函数的例子.

2.2 物态方程主线

以物态方程pV＝nRT为主线，由图2可以联想到和温度相关的关系式.分别是焦耳定律内容及焦耳系数的物理意义、绝热过程的泊松方程pVγ＝C以及另外两个等式、卡诺循环的定义以及热机效率等问题、降温方法有节流和绝热膨胀，需要掌握两个偏导数分别是及其物理意义（给出了和物态方程和热容的关系），其他细节问题留给学生补充.

图2 以物态方程为主线联想记忆脉络图

2.3 熵主线

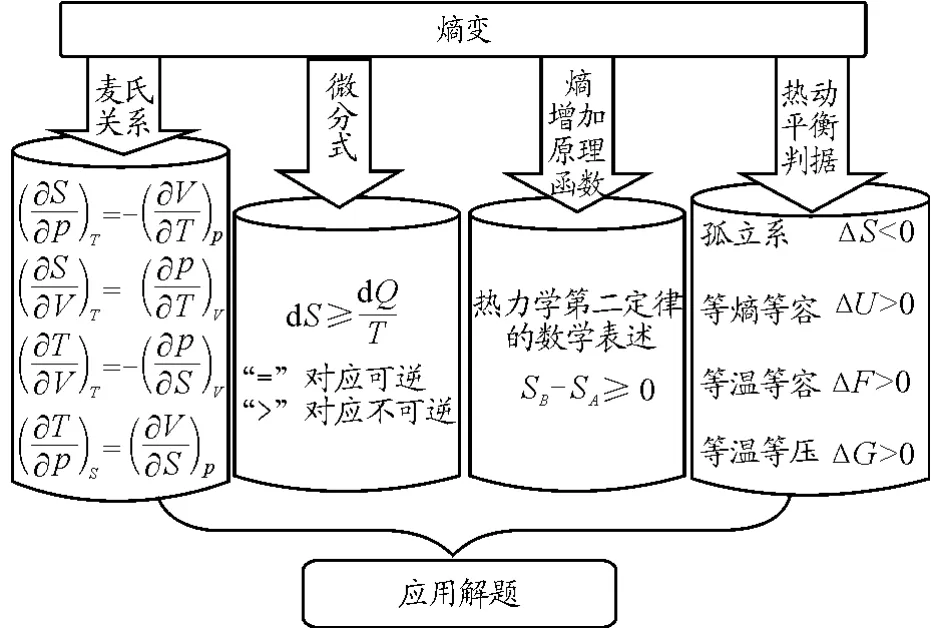
图3 以熵为主线联想记忆脉络图

如图3所示，由熵变可以想到的关键词：麦氏关系、微分式、熵增加原理、热动平衡判据.麦氏关系可以把实验不可测量的熵的导数转变成可测量导数形式.由熵的变化可以联想到表达式对相关内容的深入理解.由孤立系的平衡熵判据熵永不减小，可以联想到自由能判据、吉布斯函数判据以及内能判据.扩展其他细节问题由学生们自己完成.

3 简单应用

把以上的联想记忆脉络图应用到考试中常见的两道题.

【例1】下列关于化学势的各式中不正确的是

【例2】在等温等容的条件下，系统中发生的不可逆过程，包括趋向平衡的过程，总是朝着哪种进行

A.F增加的方向 B.G减少的方向

C.G增加的方向 D.F减少的方向

解题思路：记住图1（b）中的关系，直接可以选出例1答案应该是B，因为该项下角标标示错误.记住图3中4种热动平衡判据，等温等容时自由能永不增加，例2直接选出答案是D.类似题型都可以很快得出答案.

4 结束语

在热力学统计物理课程中，经常涉及到很多复杂的关系式，而且必须熟记.在教学中，找出其中的内在联系，给出脉络图，然后让学生们自己补充细节知识，有助于学生们对知识的深层次理解并记住这些枯燥公式，这样必将大大降低学习难度并提高学生们的学习兴趣，从而取得良好的课堂学习氛围和教学效果.

1 汪志诚.热力学与统计物理（第五版）.北京：高等教育出版社，2013.8～9

2 塔金星.浅谈麦克斯韦热学关系式的记忆与应用.物理与工程，2006，16（6）：56～58