半潜船振动特性

陈志强，周 力

(1．大连测控技术研究所，辽宁 大连116013;2．大连理工大学 运载学部，辽宁大连116024)

半潜船振动特性

陈志强1，周 力2

(1．大连测控技术研究所，辽宁 大连116013;2．大连理工大学 运载学部，辽宁大连116024)

利用Patran软件建立某半潜船有限元模型，应用Nastran软件的Lanczos方法计算此半潜船在不同载况下船舶总体垂向振动各阶模态。将计算得到的各载况下固有频率与该船主机和螺旋桨激励频率进行比较得出此半潜船振动性能良好。附连水质量对于半潜船各载况下的固有频率有十分重要的影响，因此将以源汇分布法为代表的数值计算方法与刘易斯法为代表的经验公式方法进行验证和对比，得出半潜船下潜状态的附连水质量计算应该应用数值计算方法的结论。本文对于半潜船振动设计预报及附连水质量计算具有一定的参考意义。

半潜船;振动;模态;固有频率

0 引言

半潜船是一种能够通过改变自身下潜上浮状态来运输超长超重又无法分割吊运的超大型货物 (如海上石油钻井平台、大型舰船、潜艇、龙门吊、预制桥梁构件等)的新型特种海运船舶。由于海洋石油开发和海底通信光缆的铺设等需求日益增多导致半潜船的需求十分巨大，具有极高的经济价值。目前，世界上只有少数几个国家具备半潜船的设计制造能力。国内对于半潜船的研究主要有冯志根［1］关于半潜船船型特点及其发展前景的研究，作者在文中阐述了半潜船特殊的船体结构。陈伟等［2］研究半潜船完整稳性，对“发展之路”号半潜船在几个典型工况下的大倾角稳性进行分析。郝威巍等［3］应用概率法对“发展之路”号半潜船破舱稳性进行了研究。陈华伊［4］对“泰安口”和“康盛口”号半潜船技术设计和生产设计出现的问题进行研究。焦宇清［5］介绍了50 000 DWT，半潜船的一些常识性概念和理论以及半潜船运输市场的现实状况和发展前景。桂满海［6］对20 000吨级自航半潜船Wish Way(“希望之路”)的基本设计和详细设计情况进行论述，指出半潜船下潜和上浮过程是半潜船强度和稳性计算的重点和关键技术之一。

由于半潜船的载况十分复杂，船体结构比较特殊，其振动特性分析非常重要。

1 简介

1.1 全船三维有限元模型的分析方法

在船舶总振动分析中应用有限单元法时，首先要把船体结构离散成很多单元 (杆元、梁元、膜和板元等)，通过节点的连接构成计算模型，利用有限元程序计算出各个单元刚度矩阵，再组装构成整个船体结构刚度矩阵，同时采用相同的方法构成质量矩阵，从而使自由振动问题归结为求解广义特征值问题，由此便求得船体梁固有频率和振型［7］。

全船三维有限元模型与二维模型相比更接近于船舶实际结构，对于半潜船总体振动分析更加适合。

1.2 附连水质量计算

刘易斯 (F W Lewis)方法计算附连水质量理论［8］。

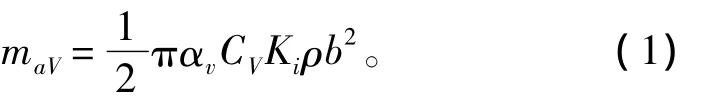
式中：ρ为水的密度;b为计算剖面处的水线半宽;d为计算剖面处的吃水;CV为垂向振动时，船舶水下部分剖面形状不同于椭圆而引入的无因次修正系数，取决于宽度与吃水之比2b/d和浸没剖面面积系数β，β=S/2bd，S为浸没剖面面积;Ki为三维流动引入的无因次修正系数，对垂向振动 (水平振动)，与船的长宽比L/B(船长吃水比L/d)及振动协调数有关;αv为浅水修正系数，和水深与剖面水线半宽之比值有关。

源汇分布法计算附连水质量理论［9］。假定在二维剖面在水中运动过程中，不计自由液面上升和兴波等因素的影响，则问题可以简化为无限水域内二维剖面在水中运动问题。本文采用源汇分布法对任意形状的二维剖面的附加质量进行求解。

设流场为无限水域，假定流体是不可压缩、均质和无粘性的理想流体，流动是无旋的有势运动，则流场存在速度势函数Φ。由于流体是不可压缩的，速度势Φ在整个流体域内满足连续方程，可以得到控制方程，即拉普拉斯方程：

同时，还应满足底部条件［B］、线性自由表面条件［F］、物面条件［S］和远方辐射条件［R］。这里自由表面条件采用高速时的近似式，具体如下：

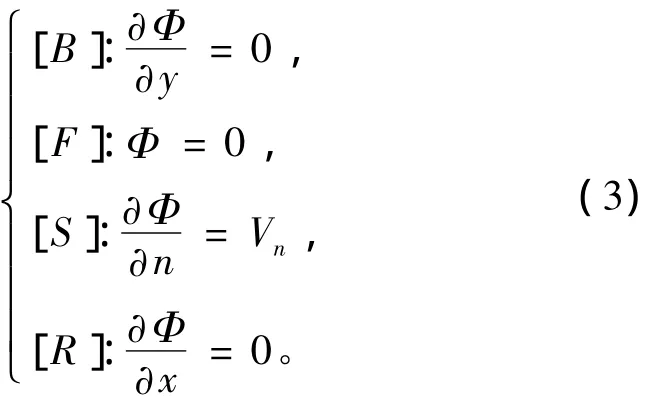
满足控制方程式(2)和式(3)的边界条件，即可构成定解问题，对速度势Φ进行求解。本文采用源汇分布法对速度势Φ进行求解。

设p(x，y)为流场内的任意一点，q(ξ，η)为点源所在的位置。二维物体剖面周围的流场速度势Φ可以表示为：

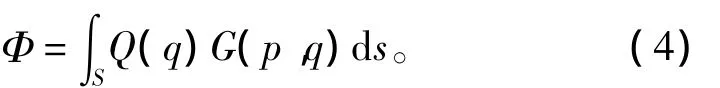
式中：Q(q)为点q处的源强;G(p，q)为二维无限水深格林函数，其满足拉普拉斯方程以及底部条件［B］、线性自由表面条件［F］和远方辐射条件［R］，表达式为：

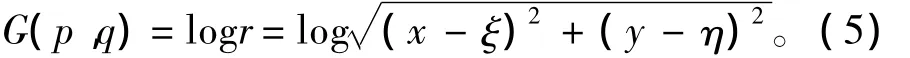
根据物面条件［S］可知：

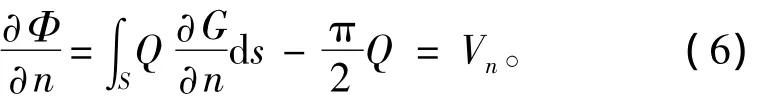
假设将流体域边界划分为N个线元Sj，且将每个线元上分布的源强Q视为常数，则速度势的积分方程可以离散为：

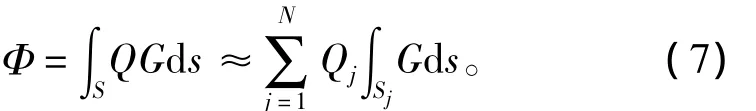
每个线元上控制点的速度势Φi可以表示为：

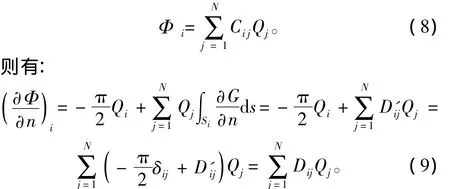
根据速度势所需要满足的边界条件，可得代数方程组：

进一步地，可将上式表示为：

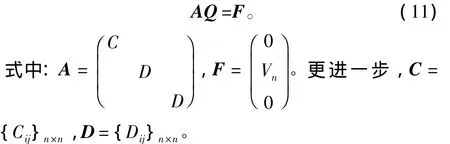
求解上式，即可得到源强Q和速度势Φ，进而可得附加质量

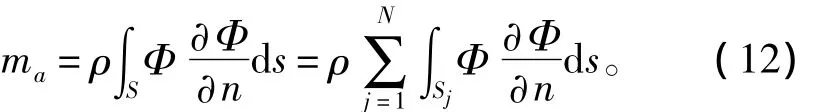
根据以上推导结果，用Fortran语言编制了计算程序。使用该程序即可计算得到任意形状的二维剖面以某一入水速度达到某一入水深度时的附加质量ma。

2 半潜船实例

本文以“发展之路”号半潜船为例，应用源汇分布法计算其在各个载况下垂向振动的附连水质量，尤其是下潜状态时的垂向振动附连水质量，建立全船三维有限元模型，计算“发展之路”号半潜船在各个载况下垂向振动固有频率。将源汇分布法计算结果与刘易斯(F W Lewis)理论计算结果沿“发展之路”号半潜船纵向分布进行比较。将“发展之路”号半潜船在各个载况下垂向振动固有频率与主机和螺旋桨激励频率进行比较得出此半潜船振动性能良好。

2.1 “发展之路”号半潜船

“发展之路”号半潜船主尺度参数如表1所示，总布置图如图1所示。

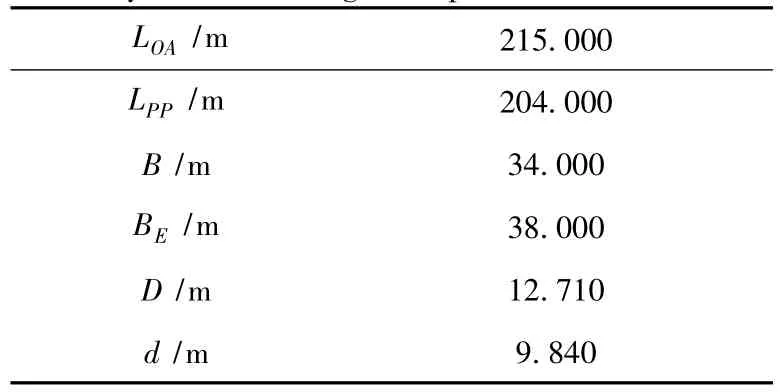
表1 “发展之路”号半潜船主尺度参数Tab.1 The principal dimension parameter of Development Way semi-submerged ship

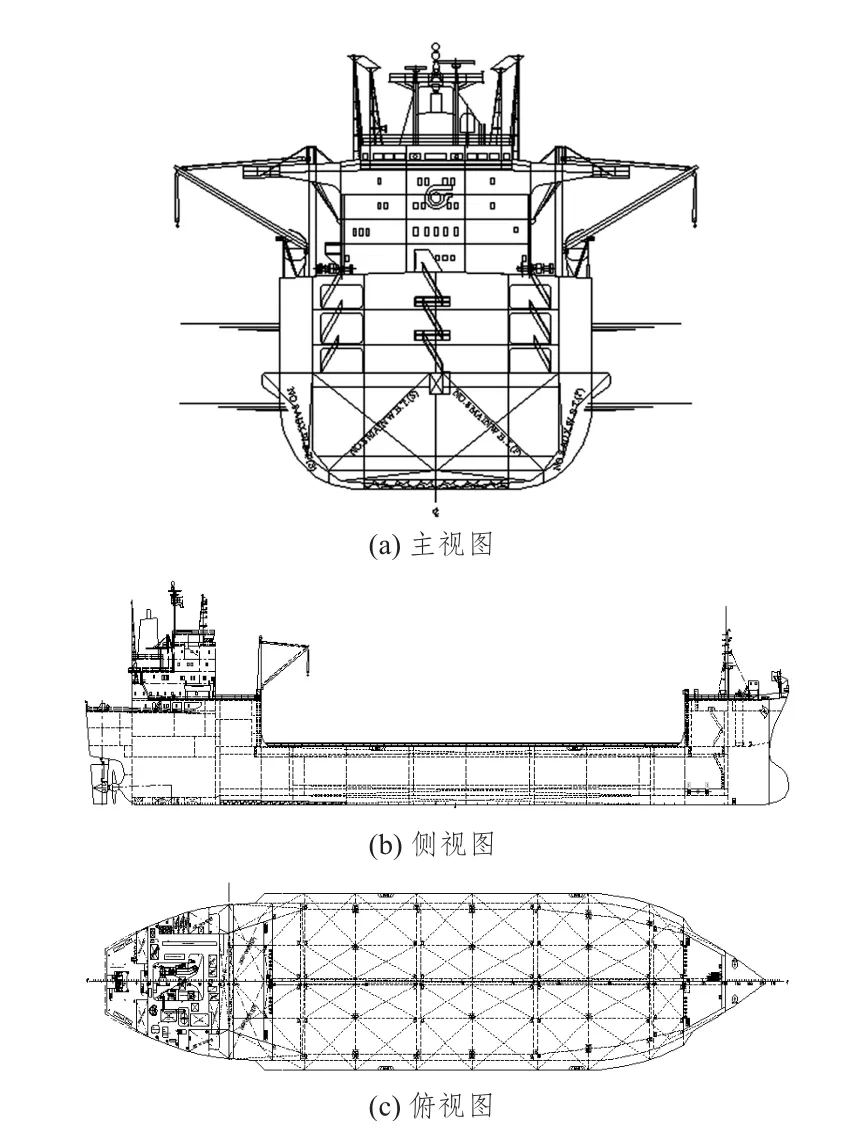
图1 “发展之路”号半潜船总布置图Fig.1 The general layout of Development Way semi-submerged ship

利用Patran软件建立“发展之路”号半潜船三维有限元模型，如图2所示。网格划分间距为0.843 m，船体的各类平板使用既能承受弯曲又能承受平面拉伸的板单元模拟，纵骨用空间梁单元模拟，主机撑杆用杆单元模拟，主机用集中质量单元模拟。本船有限元模型共有256 330个节点，527 472个单元，半潜船中纵剖面结构有限元模型如图3所示。

图2 “发展之路”号半潜船有限元模型Fig.2 The FEM model of Development Way semi-submerged ship

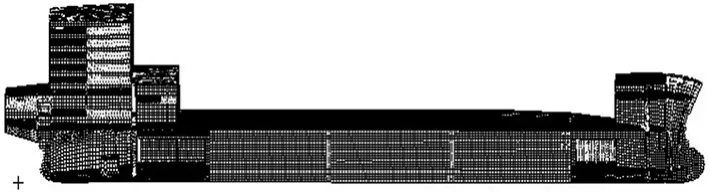
图3 “发展之路”号半潜船中纵剖面结构有限元模型Fig.3 The longitudinal section FEM model of Development Way semi-submerged ship

2.2 “发展之路”号半潜船干模态振动分析

按照全自由梁理论计算半潜船干模态固有频率。

根据两端全自由梁固有频率计算公式：

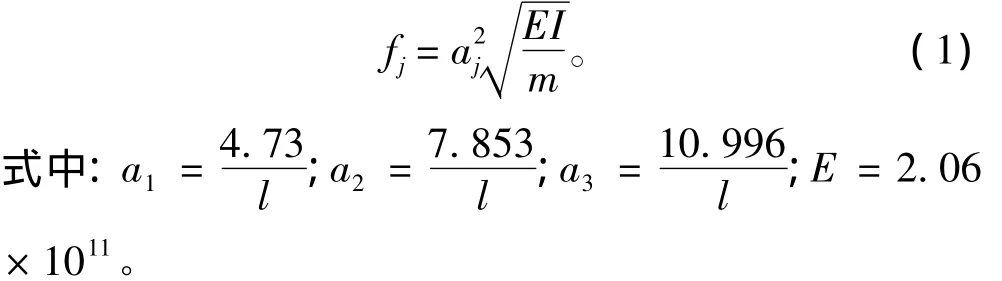
倾斜实验可知，半潜船的空船重量为19 034 t。船体梁横剖面对其水平中和轴的惯性矩I=143.3 m4。

垂向第1阶振动固有频率：

垂向第2阶振动固有频率：

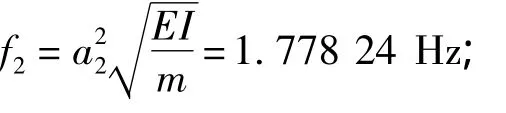
垂向第3阶振动固有频率：

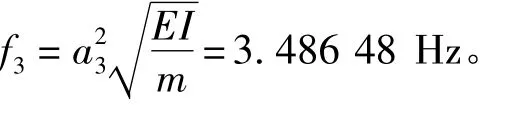
参与船体梁剖面模数计算的纵向构件如图4所示。

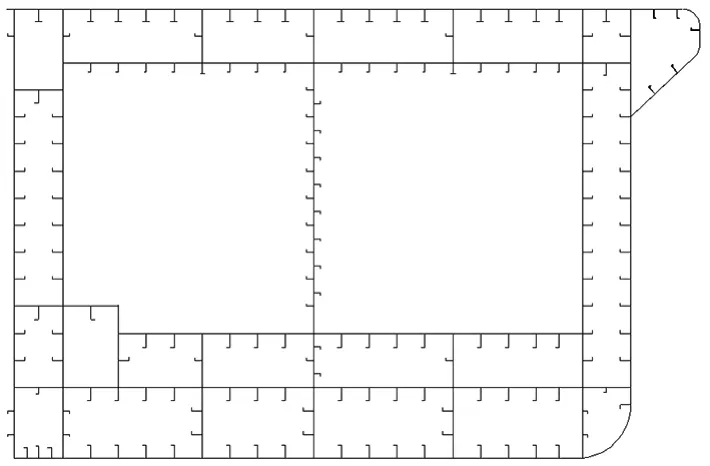
图4 “发展之路”号半潜船船体梁剖面纵向构件Fig.3 The longitudinal ship girder structure of Development Way semi-submerged ship

应用Nastran软件的Lanczos方法［10］，进行结构模态分析，计算得到结果如表2所示。

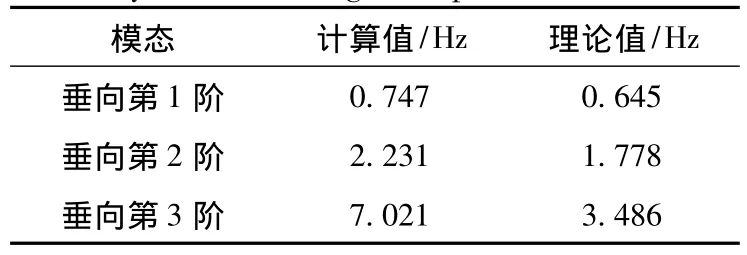
表2 “发展之路”号半潜船干模态振动分析结果Tab.2 The dry mode vibration analysis of Development Way semi-submerged ship

“发展之路”号半潜船干模态垂向前3阶振动振型图如图5所示。

图5 “发展之路”号半潜船干模态垂向前3阶振动振型图Fig.5 The first three dry mode vertical vibration frequency of Development Way semi-submerged ship

2.3 “发展之路”号半潜船压载吃水状态下结构振

动模态分析

“发展之路”号半潜船在压载状态下的吃水为3.858 m，Fortran语言计算程序计算“发展之路”号半潜船压载状态垂向附连水质量为59 609.16 t，如表3所示。

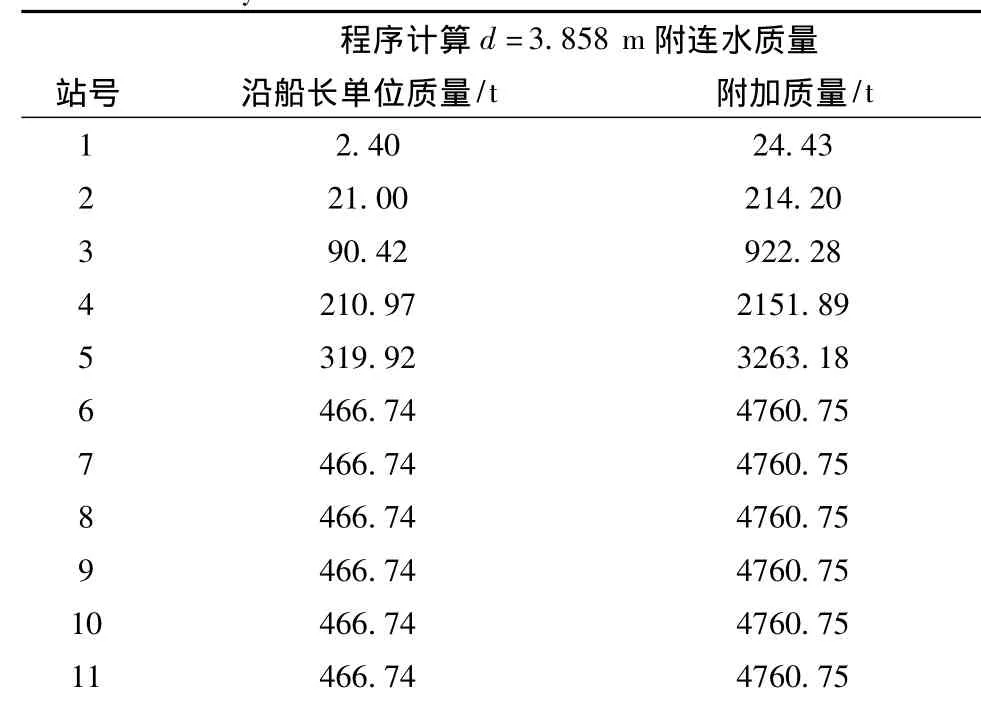
表3 源汇分布法程序计算压载状态时垂向附连水质量分析结果Tab.3 The ballast working condition vertical add mass weight analysis in source-sink method

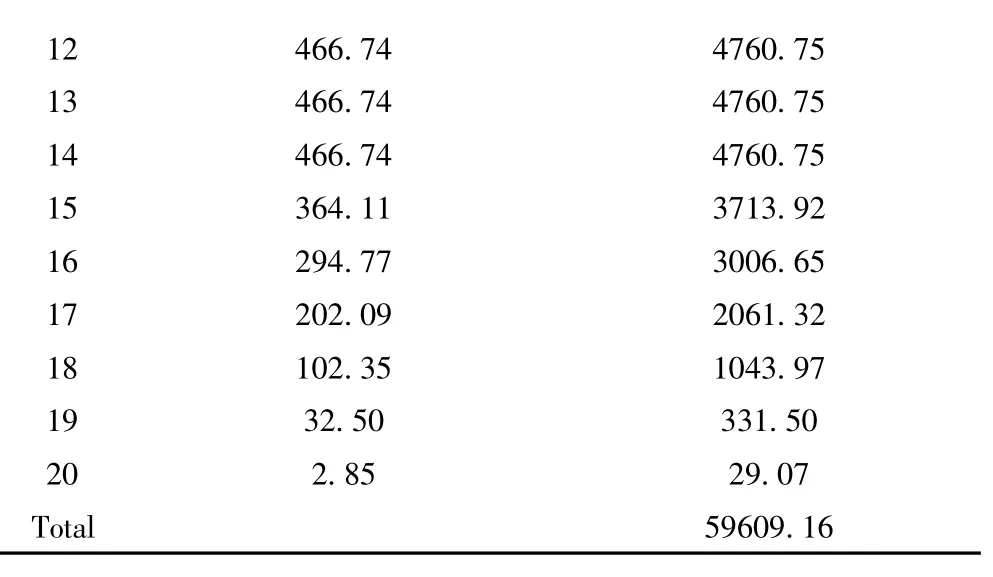
12 466.74 4760.75 13 466.74 4760.75 14 466.74 4760.75 15 364.11 3713.92 16 294.77 3006.65 17 202.09 2061.32 18 102.35 1043.97 19 32.50 331.50 20 2.85 29.07 Total 59609.16

为了求出“发展之路”号半潜船在空载状态下船体振动各阶频率，并保证船体重心保持不变，本文采用改变船体各部分构件密度的方法来计算，结果如表4所示。

表4 “发展之路”号半潜船压载模态振动分析结果Tab.4 The ballast working condition vibration analysis of Development Way semi-submerged ship

半潜船压载状态垂向前3阶振动振型图如图6所示。

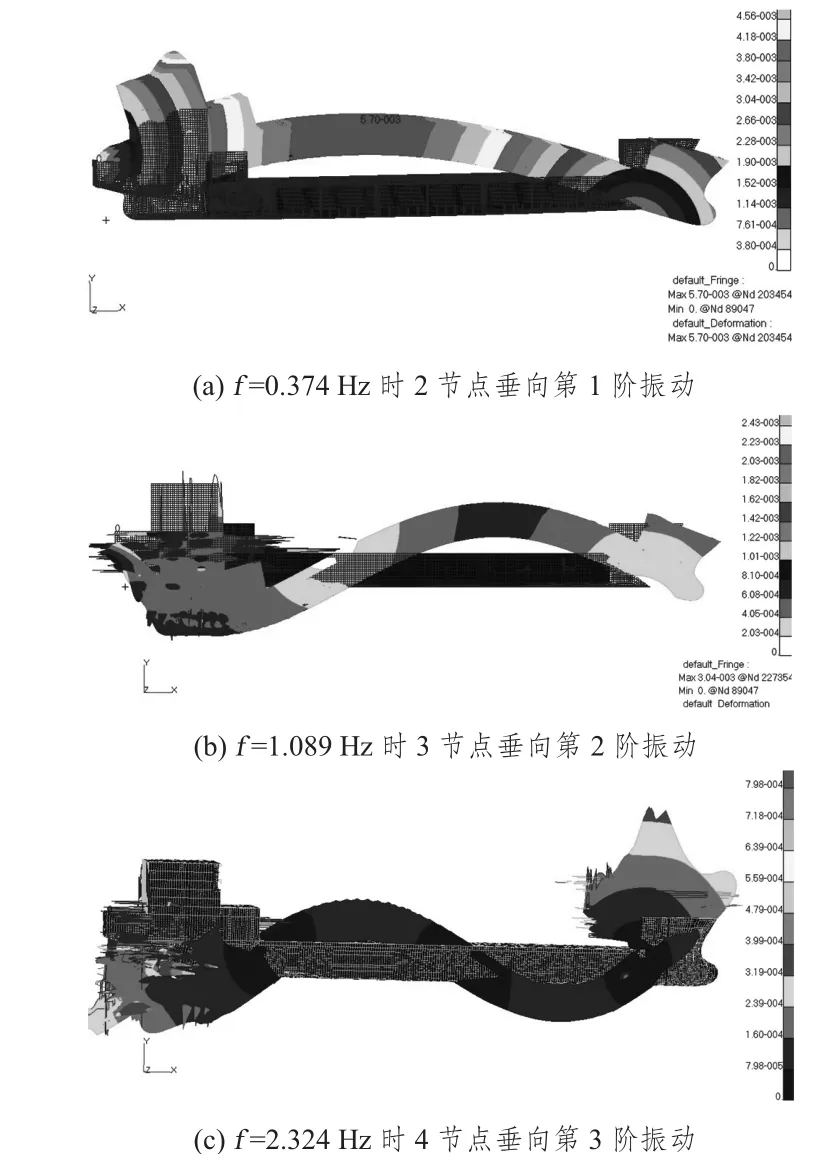
图6 “发展之路”号半潜船压载状态垂向前3阶振动振型图Fig.6 The first three ballast working condition vertical vibration frequency of Development Way semi-submerged ship

2.4 “发展之路”号半潜船设计吃水状态下结构振动模态分析

“发展之路”号半潜船在设计吃水状态下的吃水为9.3 m，载重量为50 321 t。应用Fortran语言计算程序计算0站到20站间垂向振动附连水质量为64 977.47 t，如表5所示，设计吃水状态振动模态分析结果如表6所示。

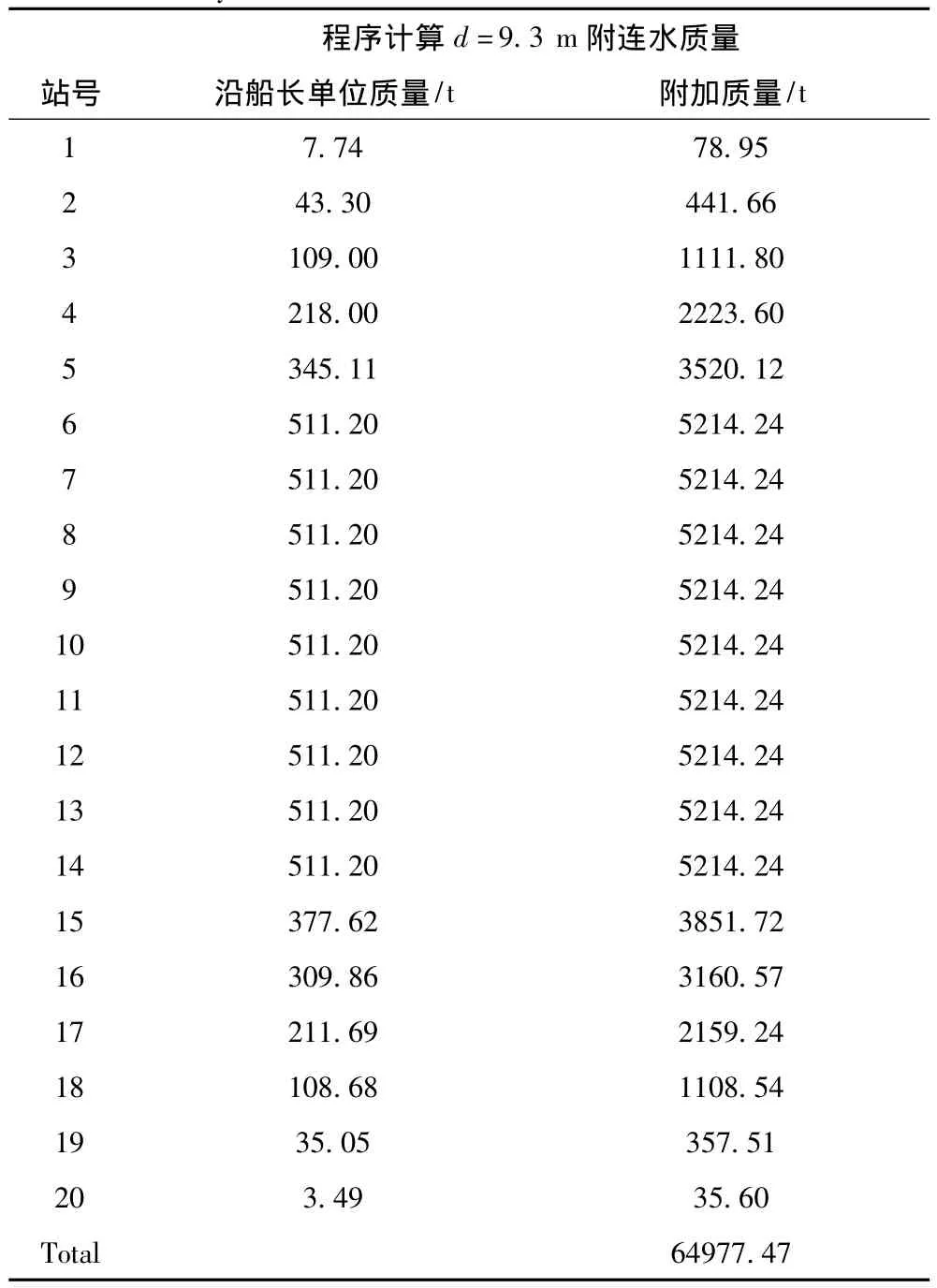
表5 源汇分布法程序计算设计吃水状态时垂向附连水质量分析结果Tab.5 The design working condition vertical add mass weight analysis in source-sink method

表6“发展之路”号半潜船设计吃水模态振动分析总结Tab.6 The design working condition vibration analysis of Development Way semi-submerged ship

“发展之路”号半潜船设计吃水状态垂向前3阶振动振型图如图7所示。

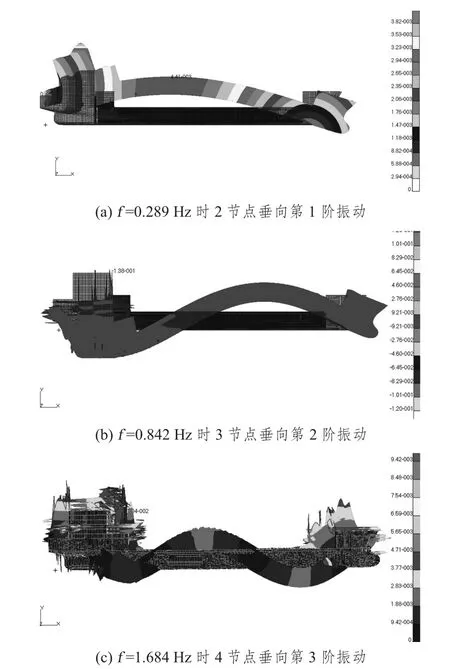
图7“发展之路”号半潜船设计吃水模态垂向前3阶振动振型图Fig.7 The first three design working condition vertical vibration frequency of Development Way semi-submerged ship

2.5 “发展之路”号半潜船下潜状态下结构振动模态分析

“发展之路”号半潜船在下潜状态下的吃水为18 m，载重量为82 526 t。应用Fortran语言计算程序计算0站到20站间垂向振动附连水质量为113 587.09 t，如表7所示，下潜状态振动模态分析结果如表8所示。

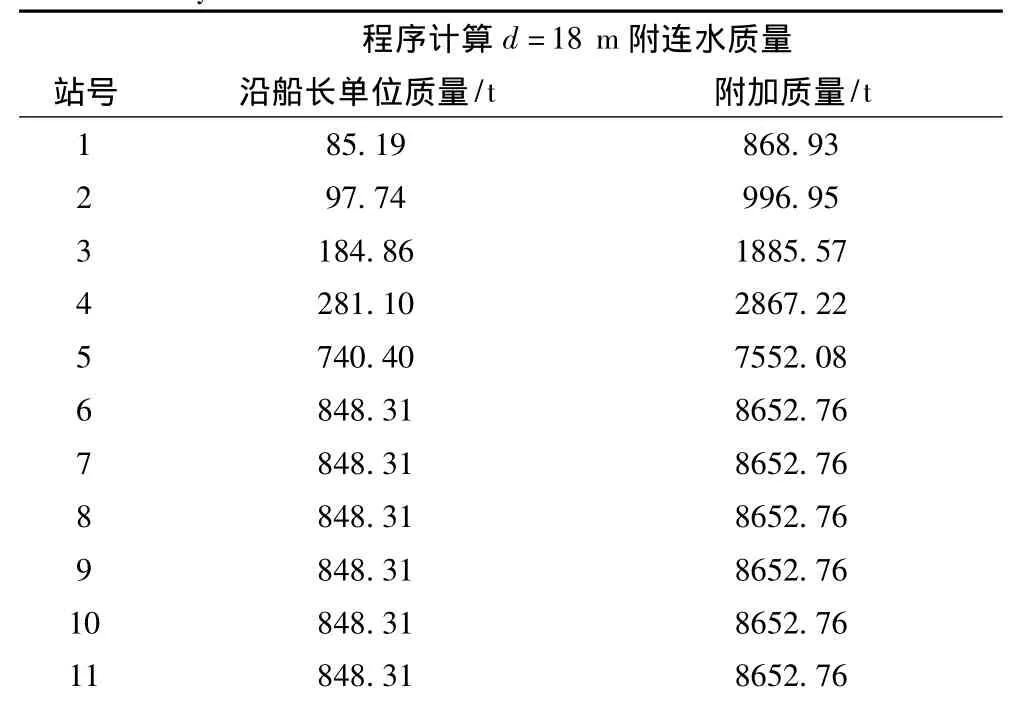
表7 源汇分布法程序计算下潜状态时垂向附连水质量分析结果Tab.7 The submergence working condition vertical add mass weight analysis in source-sink method

12 848.31 8652.76 13 848.31 8652.76 14 848.31 8652.76 15 767.92 7832.78 16 697.03 7109.71 17 482.54 4921.91 18 117.68 1200.34 19 39.96 407.59 20 6.78 69.16 Total 113587.09

表8 半潜船下潜状态模态振动分析结果Tab.8 The submergence working condition vibration analysis of Development Way semi-submerged ship

“发展之路”号半潜船下潜状态垂向前3阶振动振型图如图8所示。

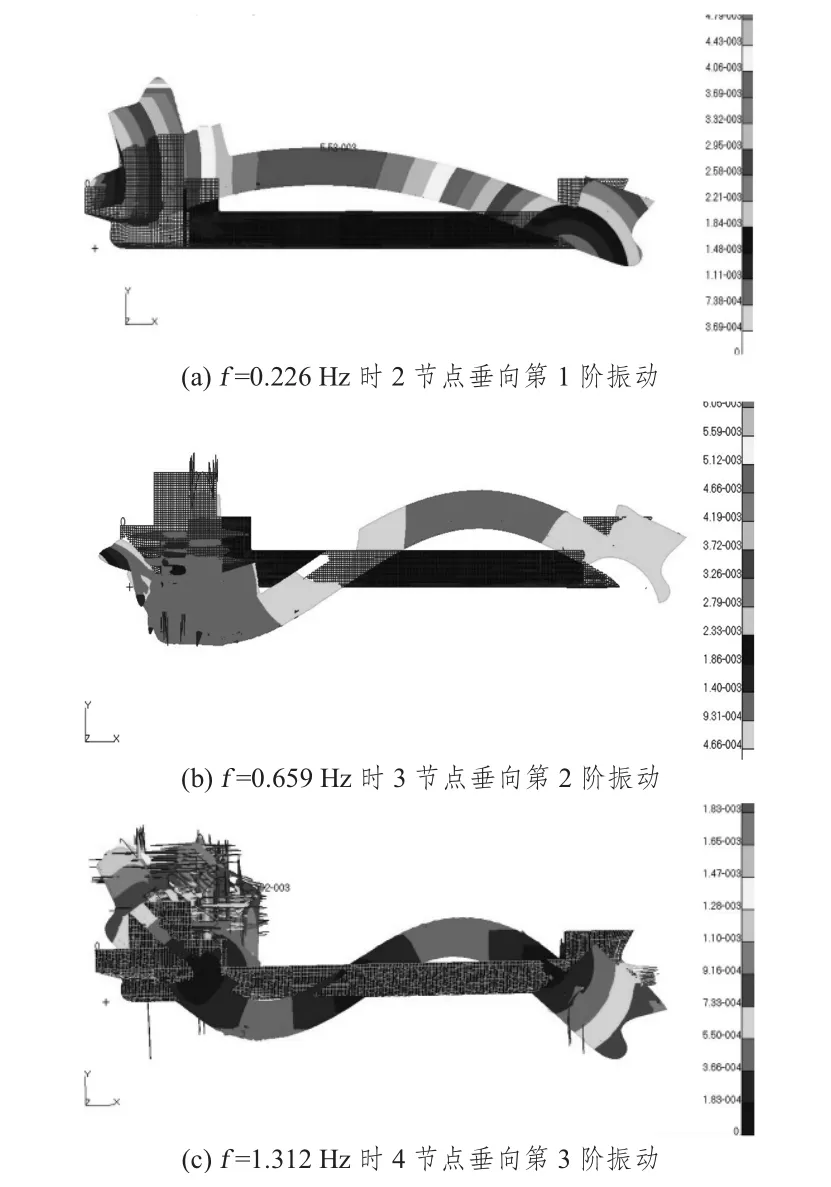
图8“发展之路”号半潜船下潜状态垂向前3阶振动振型图Fig.8 The first three submergence working condition vertical vibration frequency of Development Way semi-submerged ship

2.6 “发展之路”号半潜船振动模态分析

刘易斯 (F W Lewis)方法与源汇分布法计算“发展之路”号半潜船附连水质量沿船长方向变化对比如图9所示。

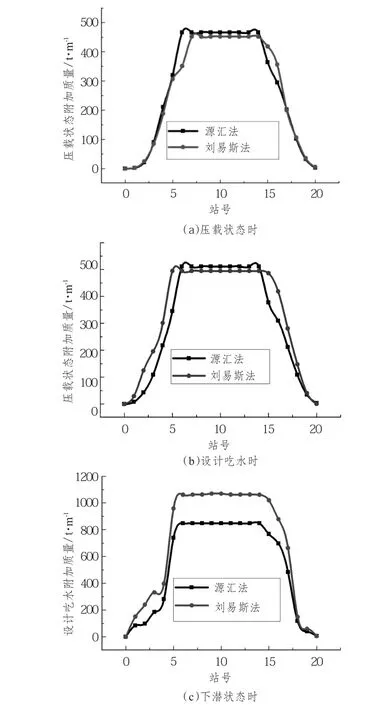
图9 源汇法与刘易斯法计算附加质量沿船长方向变化示意图Fig.9 The sketch of changing along ship length of Lewis and source-sink method add mass water weight

“发展之路”号半潜船在各个载况下，船体垂向振动模态分析结果如表9所示。

表9 “发展之路”号半潜船垂向振动模态分析结果Tab.9 The vertical vibration sum-up analysis of Development Way semi-submerged ship

半潜船主机工作转数为450 r/m，螺旋桨叶频为7.5 Hz。

通过对比可以得出以下结论：

1)普通运输船首尾和船中总体垂向振动的振型比较大，而半潜船由于首尾横剖面较大，其首尾总体垂向振动的振型比较小而船中比较大。半潜船进行模态分析时不可以按照一根直梁来进行考虑，应该应用三维有限元的方法进行分析。

2)“发展之路”号半潜船在各载况下船舶总体垂向振动1阶固有频率均低于0.5Hz，容易与波浪的激励频率遭遇而引发共振。

3)计算半潜船压载状态和设计吃水状态附连水质量可以应用刘易斯 (F W Lewis)方法，而对于半潜船下潜状态应该应用数值计算方法如源汇分布法来计算附连水质量，因为刘易斯 (F W Lewis)公式在计算半潜船中部载货甲板区全部下潜到水面以下时不适用。

4)半潜船附连水质量对船体振动具有十分重要的影响，计入附连水质量后半潜船固有频率下降十分明显。由于主机与螺旋桨激励频率与半潜船各个装载工况下的固有频率相差十分悬殊，不会激起共振。半潜船的总体垂向振动频率远低于其主机和螺旋桨的激励频率，但是容易与波浪的频率遭遇，这就需要在选取半潜船的航区和航线时考虑海域的海况。

［1］冯志根．半潜船船型特点及其发展前景［J］．上海造船，2006(1)：49－51．

FENG Zhi-gen．Characteristic of semi-submerged ship and Its development prospects［J］．Shanghai Shipbuilding，2006(1)：49－51．

［2］陈伟，宗智，林哲，等．半潜船完整稳性的初步研究［J］．中国舰船研究，2009(3)：13－17．

CHEN Wei，ZONG Zhi，LIN Zhe，et al．A preliminary study on intact stability of semi-submersible vessel［J］．Chinese Journal of Ship Research，2009(3)：13 －17．

［3］郝威巍，宗智，林哲，等．半潜船概率破舱稳性浅析［J］．中国舰船研究，2009(8)：12－17．

HAO Wei-wei，ZONG Zhi，LIN Zhe，et al．Analysis on damage stability of semi-submersible vessel using probability method［J］．Chinese Journal of Ship Research，2009(8)：12－17．

［4］陈华伊．浅谈18 000 t半潜船结构设计特点和解决的问题［J］．广船科技，2002(2)：17－19．

［5］焦宇清．50 000 DWT半潜船总体设计综述［J］．船舶设计通讯，2009(3)：51－57．

［6］桂满海．半潜船总体性能设计［J］．上海造船，2011(2)：15－17．

［7］姚熊亮．船体振动［M］．哈尔滨：哈尔滨工程大学出版社，2008．

［8］陈志坚．舰艇振动学［M］．北京：国防工业出版社，2010．

［9］贾敬蓓．三体船型阻力和运动性能试验研究［D］．大连：大连理工大学，2010．

［10］MSC Documentation2．The shifted block Lanczos method［Z］．2004．

Vibration characteristics analysis of semi-submerged ship

CHEN Zhi-qiang1，ZHOU Li2
(1．Dalian Measurement and Control Technology Research Institute，Dalian 116013，China;2．Dalian University of Technology，The Faculty of Vehicle Engineering and Mechanics，Dalian 116024，China)

Use Patran software build FEM modal of the semi-submerged ship，apply Lanczos method of Nastran software to calculate the ship's modes of global vertical vibration in several loading cases．Compare the ship's natural frequency in several loading cases to its main engine and propeller's excitation frequency，and draw the conclusion that vibration performance of this semi-submerged ship is acceptable．The calculation of added mass water has very important influence of semi-submerged's natural frequency in several loading cases，so compare the numerical calculation method such as the source distribution method with the empirical formula method such as F W Lewis method，and get the conclusion that the calculation of added mass water of semi-submerged ship's dive load condition should use the numerical calculation method．This paper has certain reference meaning to vibration prediction and calculation of added mass water of semi-submerged ship．

semi-submerged ship;vibration;mode;natural frequency

U674．941

A

1672－7649(2014)06－0031－07

10.3404/j.issn.1672－7649.2014.06.006

2013－02－25;

2013－05－28

陈志强(1984－)，男，助理工程师，从事船体振动与噪声测试与减振降噪研究。