夹层板面内连接结构力学性能数值仿真分析

王 果，胡宗文，王自力，张延昌

(1.江苏科技大学船舶与海洋工程学院，江苏镇江212003;2.中国船舶及海洋工程设计研究院，上海200011)

夹层板面内连接结构力学性能数值仿真分析

王 果1，2，胡宗文1，王自力1，张延昌2

(1.江苏科技大学船舶与海洋工程学院，江苏镇江212003;2.中国船舶及海洋工程设计研究院，上海200011)

夹层板连接结构始终制约着夹层板在船体结构中的大规模应用。为推进夹层板连接结构的研究设计，以夹层板面内连接结构为研究对象，研究面内连接结构屈服强度、稳定性、极限强度分析的力学模型，然后从建模方式、单元类型、网格尺寸、加载速率、初始缺陷等多个方面研究面内连接结构力学性能数值仿真分析技术。通过研究确定：采用Shell－Shell－Contact建模方式，可以提高计算效率和计算精度;网格尺寸的选取应以计算资源作为主要考虑因素;可采用小尺寸板条模型研究极限强度，加载时间为5～10 T(T为结构固有周期)范围内可提高计算效率和计算精度;施加5%板壳厚度的初始缺陷，可在极限抗压能力分析时引导结构进入一阶屈曲模态。

夹层板;面内连接结构;力学性能;数值仿真

0 引言

金属折叠式夹层板重量轻、比强高、抗冲击性能优良，具有防振、防火等诸多优点，目前已在航空、航天、飞机、汽车、桥梁等领域广泛应用［1，3］。夹层板在船舶结构中使用不仅可以有效解决常规船体结构设计中的瓶颈问题，同时也可以提高舰船抗冲击性能，提高舰船设计水平。因此，近年来各国海军、船级社、科研院所等已陆续开展夹层板制造、性能、设计等方面的研究工作［4－8］，目的在于设计出性能优良、成本低廉、更可靠、更安全的船舶结构。

目前国内外的学者对金属折叠式夹层板的研究更多关注于夹层板本身的力学性能，考虑的研究对象主要是夹层板梁单元或是夹层板本身，而且一般认为夹芯与面板的连接为理想连接，忽略阻碍夹层板在船体结构中应用的夹层板与夹层板之间、夹层板与传统加筋船体结构之间的连接过渡问题［6－9］。目前由于各国在该方面研究成果保密等原因，金属折叠式夹层板结构的实际制造加工、夹层板连接结构设计及实船应用方面公开的研究成果及应用实例相对较少［2，5，10］;国内目前该领域的研究工作基本处于空白阶段。为推进国内对船用夹层板连接结构的设计研究工作，本文将在夹层板面内连接结构屈服强度、稳定性和极限强度的力学模型的基础上，系统研究不同的单元类型、建模方式、网格尺寸、加载速率及初始缺陷因子等对各力学性能计算结果的影响;提出合理有效的面内连接结构力学性能数值仿真分析技术。

船体结构主要是板、梁结构形式，主要承受横向、面内载荷，其力学性能主要包括屈服强度、稳定性和极限强度。夹层板在船体结构中应用代替传统加筋板架，因此夹层板船体结构 (采用夹层板及夹层板连接结构的船体结构称为夹层板船体结构［11］)的主要力学性能同样包括屈服强度、稳定性和极限强度3个方面。本文主要研究夹层板面内连接结构各力学性能分析的力学模型和连接结构力学性能数值仿真技术为夹层板面内连接结构力学性能分析及设计提供技术指导。

1 力学模型

1.1 屈服强度

对于应用于舰船上层建筑甲板板架中的夹层板船体结构而言，可根据国军标 (GJB4000)§102.3.7［12］中对排水型水面舰船上层建筑的强度校核的要求进行屈服强度校核对比研究。

力学模型如图1所示。选取夹层船体结构中强框架支撑的板格单元作为研究对象。采用面内连接结构的夹层板船体结构主要承受横向载荷、面内载荷。参考国军标 (GJB4000)中对舰船上层建筑强度的要求，取P=4.91 kPa作为设计载荷，板格由强框架支撑，四周采用刚性固定边界条件。

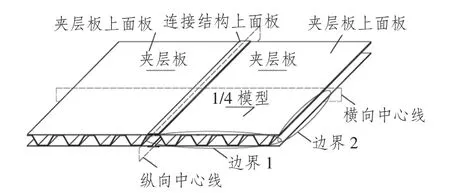
图1 力学模型示意图Fig.1 The diagram of mechanical model

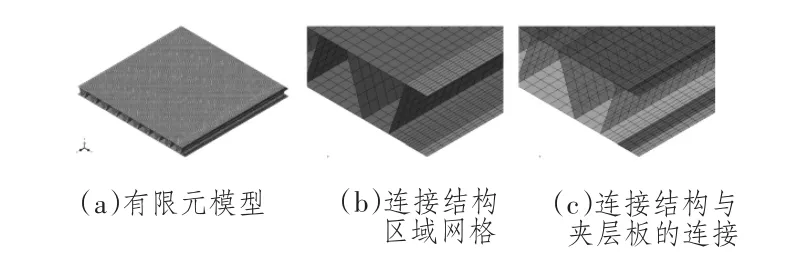
图2 夹层板船体结构有限元模型Fig.2 The finite element model of sandwich ship structure

有限元模型选取1/4对称模型进行数值仿真分析计算。基于Abaqus采用Shell单元建立有限元模型，网格尺寸范围为15～20 mm，如图2所示。夹层板与连接结构之间连接的建模技术，将在2.1节中详细叙述。边界1和边界2(见图1)采用刚性固定，中心线处分别采用对称边界约束。

材料模型的结构材料采用船用低碳钢Q235，认为结构材料为理想弹塑性材料。弹性模量E=2.1×105MPa，泊松比0.3。

1.2 稳定性

夹芯层和连接结构沿纵向布置，因此夹层船体结构在横向 (垂直于焊缝的方向为横向［11］)与纵向(夹芯单元的长度方向即焊缝方向为纵向［11］)2个方向的刚度不同，采用全尺寸有限元模型分别研究轴向载荷作用下连接结构的横向与纵向屈曲模态。有限元模型如图3所示，借助于通用接触定义结构的自接触，结构材料模型为理想弹塑性材料。

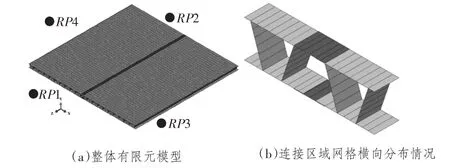
图3 稳定性计算的有限元模型Fig.3 The finite element model for stability analysis

通过耦合点RP1，RP2，RP3，RP4在加载端施加单位载荷，计算各结构纵向和横向的临界载荷。具体加载及边界条件为：①纵向稳定性。RP1：x=y=z= θy= θz=0;RP2：x=y= θy= θz=0，RP2施加z向单位载荷。②横向稳定性。RP3：x=y=z= θx= θy=0;RP4：y=z= θx= θy=0，RP4 施加x向单位载荷。

1.3 极限强度

极限强度的研究方法有直接计算法、有限元分析方法、实验研究方法等。彭大伟、胡胜谦等人［13－14］的研究表明：采用合理加载速率的准静态法计算结果与实际实验结果比较接近，能够较好的模拟结构极限承载能力。面内连接结构的极限强度主要包括极限抗压、抗弯能力，因此本文将基于准静态法分别采用小尺度结构模型对比研究连接结构横向、纵向极限抗压、抗弯能力。

基于Abaqus软件采用S4R壳单元建立有限元模型，如图4所示，借助通用接触技术定义结构的自接触。结构材料模型采用Cowper－Symonds弹塑性材料模型，考虑材料的应变率敏感影响，材料失效最大塑性应变为0.3。同样采用耦合点施加边界、载荷：①横向极限抗压、抗弯能力。RP1：x=y=z= θx= θy=0，RP2：y=z=θx=θy=0，通过RP2施加x向的位移载荷;②纵向极限抗压、抗弯能力。RP1：x=y=z=θy= θz=0;RP2：x=y= θy= θz=0，通过 RP2施加z向的位移载荷;③位移加载方式。施加轴向位移载荷研究极限抗压能力，施加角位移载荷研究极限抗弯能力。采用光滑幅值曲线加载［15］，可以保证加载曲线每个数据点处一、二阶导数均为光滑曲线，进而避免由于加载速率不连续引起的波动。分析计算极限抗压能力时还应考虑引入结构的初始缺陷。

图4 极限强度计算的有限元模型Fig.4 The finite element model for ultimate analysis

2 力学性能数值仿真分析技术

数值仿真分析方法可以较为准确的获得夹层板连接结构的各项力学性能，但建模方式、网格类型、单元尺寸、加载速率等因素的选取会对计算精度、计算效率产生不同程度的影响。因此需通过仿真技术研究确定合适的建模方式、网格类型、单元尺寸及加载速率等参数。

2.1 单元类型及建模方式

夹层板面板与面内连接结构之间采用激光焊接技术连接，由于激光焊接的特点，只能实现夹层板面板与连接结构之间在焊缝处连接，非焊缝区域存在误差间隙 (见图5)，无法实现面板与连接结构的完整连接，结构整体受到载荷作用时未焊透部位之间通过相互接触来传递载荷。在Abaqus软件中夹层板面板与连接结构之间连接可以通过绑定约束、接触定义、合并及焊缝4种处理方式，同时考虑到单元类型 (shell、solid)共有6种结构模型，具体如表1所示。采用以上6种方式建立有限元模型，与同尺寸夹层板结构 (Sandwich)力学性能进行对比分析，计算结果汇总如表2所示，各结构的载荷－位移曲线和弯矩－曲率曲线如图6所示。

图5 夹层板船体结构连接区域示意图Fig.5 The connecting region of sandwich ship structure

表1 六种有限元建模方式Tab.1 Siol kinds of finite element model

可以看出：各建模方式对应的屈服强度都基本与同尺寸夹层板结构屈服强度相当，相对误差均在5%以内，最大应力及最大变形出现的位置都相同;各建模方式对结构极限强度存在一定程度的影响，极限抗压、抗弯能力的最大相对误差分别为6.61%和12%。综合考虑，Shell－Shell－Contact建模方式具有较好的计算效率、可靠的计算精度，属于较理想的建模方式。

图6 各建模方式下的载荷(弯矩)－位移(曲率)曲线Fig.6 Force(moment)versus displacement(curvature)curves

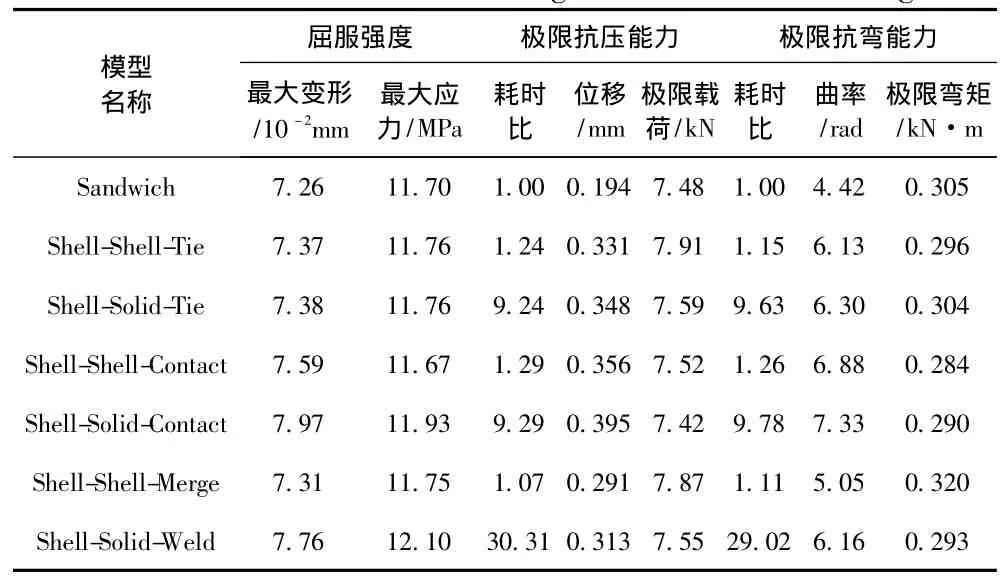
表2 各建模方式下的极限强度计算结果Tab.2 The results of ultimate strength of different modeling forms

2.2 网格尺寸

选取夹芯层高度方向的网格数分别为6，8，10，12，14五种网格密度，研究网格尺寸对力学性能的影响，计算结果如表3所示，各网格尺寸下的载荷－位移、弯矩－曲率曲线如图7所示。

表3 各网格尺寸下的屈服强度、极限强度计算结果Tab.3 The results of static strength and ultimate strength of different element size

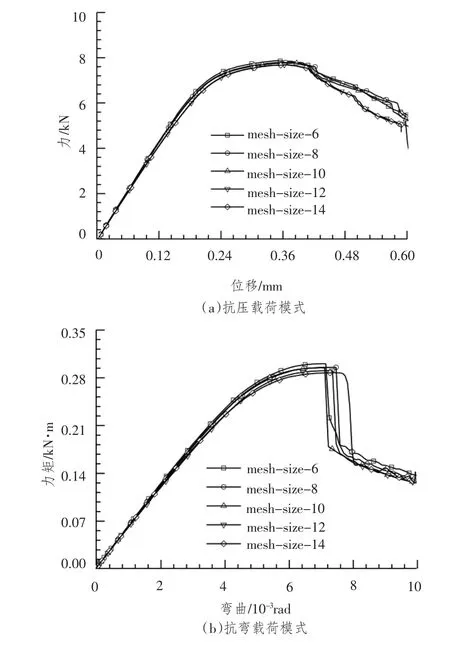
图7 各网格尺寸下的载荷(弯矩)－位移(曲率)曲线Fig.7 Force(moment)versus displacement(curvature)curves

可以看出：随着网格尺寸减小，屈服强度对应的最大应力、变形增加，而且应力增加更为明显，最大应力相差29.8%，变形相差15.5%，主要由于应力集中问题的存在，单元尺寸减小使得应力增加。随着网格尺寸减小，结构极限抗压、抗弯能力呈减小趋势，不同网格尺寸对应的极限抗压、抗弯能力相差分别为2.3%和4.5%，但网格尺寸对计算效率的影响程度明显高于计算精度的影响。因此，网格尺寸的选取应以计算资源作为主要考虑因素，对局部构件分析计算时，夹芯层高度方向选择6～8个网格既可满足精度要求又可提高计算效率。

2.3 加载速率

准静态法的计算精度和计算效率易受加载速率的影响。保持加载位移不变采用光滑幅值曲线位移加载方式［15］，分别选取加载时间 t为1 T，5 T，10 T，20 T，50 T，100 T，1 000 T进行极限抗压、抗弯能力分析，其中T为结构的固有周期。各加载速率对应的极限载荷、弯矩如表4所示，各加载速率对应的载荷(弯矩)－位移(曲率)曲线如图8所示。

表4 各加载速率下的极限强度计算结果Tab.4 The results of ultimate strength of different loading rate

可以看出：加载速率对计算精度影响较小，对计算效率影响较大。当加载时间t＜5 T时，载荷－位移曲线出现较大波动，计算过程受结构动力学因素影响较大，结构变形能占内能的10%～15%;加载时间t≥5T时，载荷－位移曲线的极限载荷基本重合，结构变形能仅占内能的2%～6%，计算过程结构动力学因素影响很小。但加载时间较长势必导致计算时间增加，影响计算效率，因此综合考虑，选取加载时间为5～10 T进行极限强度计算，可在提高计算效率的同时提高计算精度。

图8 不同加载速率对应的载荷(弯矩)－位移(曲率)曲线Fig.8 Force(Moment)versus displacement(curvature)curves

2.4 初始缺陷

连接结构在制造过程中难免存在初始缺陷，连接结构极限抗压能力计算时，通过引入结构初始缺陷可引导结构进入一阶屈曲模态。分别选取初始缺陷为0%，1%，2%，5%，10%，20%，50%，100%的结构板壳厚度进行对比研究，确定合理的初始缺陷因子。各初始缺陷因子下的载荷－位移曲线如图9所示，初始缺陷因子与极限抗压能力之间的关系曲线如图10所示。

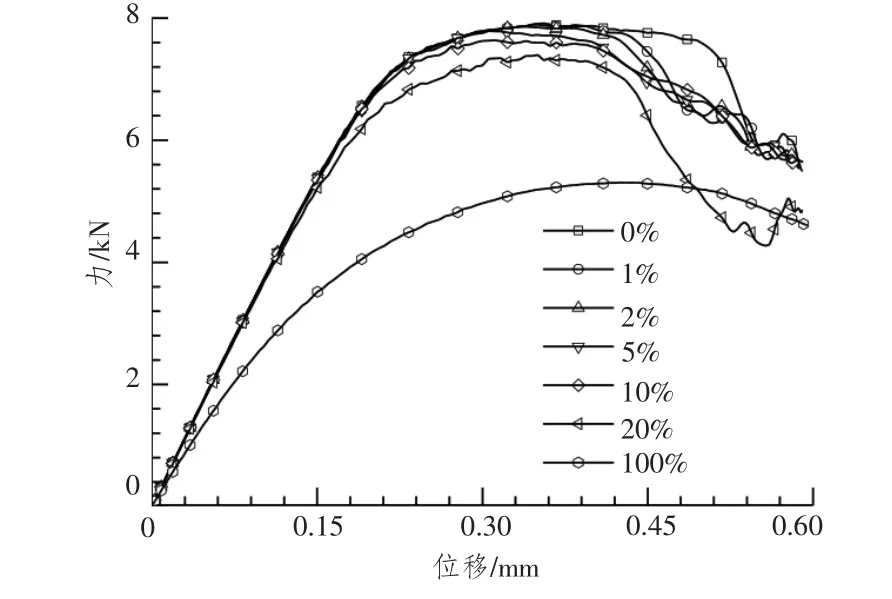
图9 各缺陷因子下的载荷－位移曲线Fig.9 Force versus displacement curves

图10 各缺陷因子下对应的极限抗压能力Fig.10 The ultimate load of different imperfection factor

可以看出：初始缺陷因子对结构极限抗压能力有一定程度的影响，初始缺陷因子为0～5%时，载荷－位移曲线基本重合，各极限载荷之间的相对误差均小于3%;初始缺陷因子大于5%时，载荷－位移曲线完全分离，极限载荷之间相对误差较大。因此计算结构极限抗压能力时选用的初始缺陷因子应不大于5%的结构板壳厚度。

3 结语

本文分析夹层板面内连接结构力学性能分析的力学模型，并分别对单元类型、建模方式、网格尺寸、加载速率及初始缺陷因子等数值仿真技术进行了较系统研究，主要结论如下：

1)夹层板面内连接结构力学性能分析时，夹层板及连接结构均采用shell单元，焊缝部位定义绑定约束 (tie)，未焊透部位定义接触作用(contact)，可在提高计算精度同时保证计算效率。

2)面内连接结构力学性能分析时，网格尺寸的选取应以计算资源作为主要考虑因素;在局部构件进行分析计算时，夹芯层高度方向选择6～8个网格既可满足精度要求又可提高计算效率。

3)采用Shell－Shell－Contact建模技术建立1/4对称模型模拟甲板板架，并根据规范要求分析研究面内连接结构的屈服强度，其中计算模型的边界条件为2个对称边界分别采用各自的对称边界，另外2个边界采用刚性固定边界。

4)采用全尺寸模型研究面内连接结构的稳定性，载荷和边界通过耦合点施加，其中在加载端施加单位载荷，另一端作简支约束，加载端放松对应加载方向自由度。

5)基于准静态法采用小尺寸横向、纵向板条模型研究面内连接结构的极限抗压、抗弯能力，采用光滑幅值曲线位移加载，加载时间在5～10 T范围内可提高计算效率和计算精度。另外，极限抗压能力分析时，施加5%板壳厚度的初始缺陷，可引导结构进入一阶屈曲变形模态。

［1］NOURY P，HAYMAN B，MCGEORGE D，et al.Lightweight construction for advanced shipbuilding－recent development［R］.The BONDSHIP and the SANDWICH European Cooperative Research Projects.

［2］STEFANICK K M.Laser welded lightweight sandwich panel and fabrication and shipyard application［R］.Concurrent Technologies Corporation.

［3］岳灿甫，吴始栋.国外船用激光焊接波纹夹芯板的开发与应用［J］. 鱼雷技术，2007，15(4)：1－5.

［4］张延昌.水下爆炸冲击载荷下折叠式夹层板防护性能研究［D］.上海：上海交通大学，2012.

［5］VINCENT C，SERDAR Y.Laser welded steel sandwich panel bridge deck development：finite element analysis and stake weld strength tests［R］.C2006－014－RPT －01，University of Maine.

［6］TILBROOK M T，RADFORD D D，DESHPANDE V S.Dynamic crushing of sandwich panels with prismatic lattice cores［J］.International Journal of Solids and Structures，2007，44：6101 －6123.

［7］ZHANG Yan－chang，ZHANG Shi－lian，WANG Zi－li，et al.Quasi－static compressive behavior of U － type corrugated cores sandwich panels［J］.Journal of Ship Mechanics［J］.Journal of Ship Mechanics，2012(12)：1417 －1426.

［8］王果，张延昌.Y型激光焊接夹层板抗爆性能分析［J］.舰船科学技术，2012，34(277)：68 －75.

WANG Guo，ZHANG Yan－chang.Analysis of the anti－shock capacity of laser－welded corrugated－Y type－core sanduich panels［J］.Ship Science and Technology，2012，34(277)：68－75.

［9］COTÉ F，DESHPANDE V S，FLECK N A，et al.The out－ofplane compressive behavior of metallic honeycombs［J］.Materials Science and Engineering A，2004，380：272 －280.

［10］Frank Roland，Thomas Reinert，Jos.L.Meyer GmbH，et al.Laser welded sandwich panels for the shipbuilding industry［R］.RINA－Bericht－ENDV－24－7－00.

［11］王果.金属折叠式夹层板连接结构设计及力学性能分析［D］.镇江：江苏科技大学，2013.

［12］中国人民解放军总装备部.舰船通用规范——1组：船体结构［S］.上海：海军论证中心标准规范所.

［13］彭大伟，张世联.结构极限强度分析的三种有限元解法研究［J］.中国海洋平台.2010，25(2)：1－5.

［14］胡胜谦.船舶损伤后船体剩余强度评估方法［D］.镇江：江苏科技大学，2012.

［15］庄茁，由小川，廖剑晖，等.基于Abaqus的有限元分析和应用［M］.北京：清华大学出版社，2009.

Numerical simulation technology for mechanical property analysis of sandwich panel connections in plane

WANG Guo1，2，HU Zong－wen1，WANG Zi－li1，ZHANG Yan－chang2
(1.School of Naval Architecture and Ocean Engineering，Jiangsu University of Science and Technology，Zhenjiang 212003，China;2.Marine Design and Research Institute of China，Shanghai 200011，China)

Sandwich panel connections always restrict the application of steel folded core sandwich panels in ship structure.In order to promote the study of sandwich panel connections research and design，mechanical models for analysis of yield strength，ultimate strength and stability will be researched in this paper.And then the numerical simulation technology of modeling methods，element size，loading methods and initial imperfection factor and so on were studied.Through these research to determine：Shell－Shell－Contact modeling method can improve the calculation efficiency and precision;selection of element size should be based on the computing resources as the main consideration factor;small size structure models can be used to research ultimate strength and loading time between 5～10 T(T is structure natural period)can improve the calculation efficiency and precision;initial imperfection factor applied 5%shell thickness on the structure can guide structure into buckling mode in analyzing the ultimate compressive capacity.

sandwich panel;connections in plane;mechanical properties;numerical simulation

U663，O344

A

1672－7649(2014)06－0054－06

10.3404/j.issn.1672－7649.2014.06.010

2014－03－17;

2014－04－09

王果(1988－)，男，硕士研究生，研究方向为船舶与海洋结构物设计制造。