转向架构架试验载荷谱编制方法
孙晶晶,孙守光,李 强,王 曦
(北京交通大学 机械与电子控制工程学院, 北京 100044)
对结构进行可靠性试验,是确保结构在规定使用条件和寿命周期内具有足够可靠性的重要检验手段。对于轨道车辆结构,在研发阶段进行的可靠性试验,通常采用国际现行标准或与之等价的国内标准中推荐的载荷[1-5]。需要指出的是:这些标准中推荐的载荷并不与运用里程直接对应,采用这些载荷给出的结构可靠性试验结果还属于定性的。
转向架构架是轨道车辆最重要的部件之一,其设计寿命一般对应着明确的运用里程;对于提速客车而言,构架设计寿命为1 200万km。由于运用条件和构架结构的复杂性,即使通过了研发阶段的可靠性试验,在实际运用中构架也可能出现可靠性不足(运用寿命达不到设计要求)的问题[6-9]。此时,需要通过改进构架结构提高其可靠性,其中的关键环节之一是对改进后的构架进行定量的可靠性考核。由于构架是依据标准中推荐载荷进行可靠性设计并通过了可靠性考核,在对运用可靠性不足的构架进行结构改进和可靠性考核时,现行标准中推荐的载荷已不适用,需要建立与实际运用条件相一致的载荷谱,才能真实再现构架在实际运用条件下的损伤情况,并与构架的运用寿命准确对应。
构架通常承受着十几个甚至几十个载荷,建立构架载荷谱是一个相当困难的工作。在用于构架可靠性定量考核的试验载荷谱建立方面,目前国际上仅有个别科研团队开展了初步的研究工作[10-11]。原因在于:①获取构架运用载荷时域历程困难;②多载荷系时域联动编谱方法还有待研究。文献[12]采用载荷解耦测试原理,建立构架运用载荷测试方法,成功获得209P构架的运用载荷时域历程,并建立完备的构架基本载荷系。本文在此基础上进一步研究多载荷系时域联动编谱方法,以建立适用于构架可靠性定量考核的试验载荷谱。
1 建立构架载荷系分立载荷谱
构架在实际运用中承受的全部载荷可以分解为若干具有自平衡特征的载荷组合,称之为构架载荷系。对于209P转向架构架,载荷系分别为浮沉载荷系Fv、侧滚载荷系Fr、扭转载荷系Fw、横向载荷系Ft、菱形载荷系Fo、纵向牵引载荷系Fl、制动载荷系Fb和蛇行载荷系Fa,其中蛇行载荷系是依据文献[12]的研究结论补充的,其他载荷系与现行标准一致。因篇幅所限,图1仅展示了构架浮沉载荷系和扭转载荷系。

图1 构架浮沉载荷系和扭转载荷系示意
获得构架运用载荷时域历程是编制构架载荷谱的基础。能否正确再现构架运用损伤是评价载荷谱编制正确与否的根本依据。构架的运用损伤取决于构架在运用过程中承受的应力历程,整个应力历程产生损伤的效果可由与运用里程相对应的规定频次的等效应力来度量。
本文以209P转向架构架为研究对象,在赤峰至大连区段运营条件下连续采集构架载荷时域历程(累积运行里程5 826 km,累积采集时长96 h)。此外,还在实验室内对构架各载荷系与典型测点应力之间的传递关系进行了标定。应力测点位置见图2。上述测试的具体过程和相关测试结果见文献[12]。
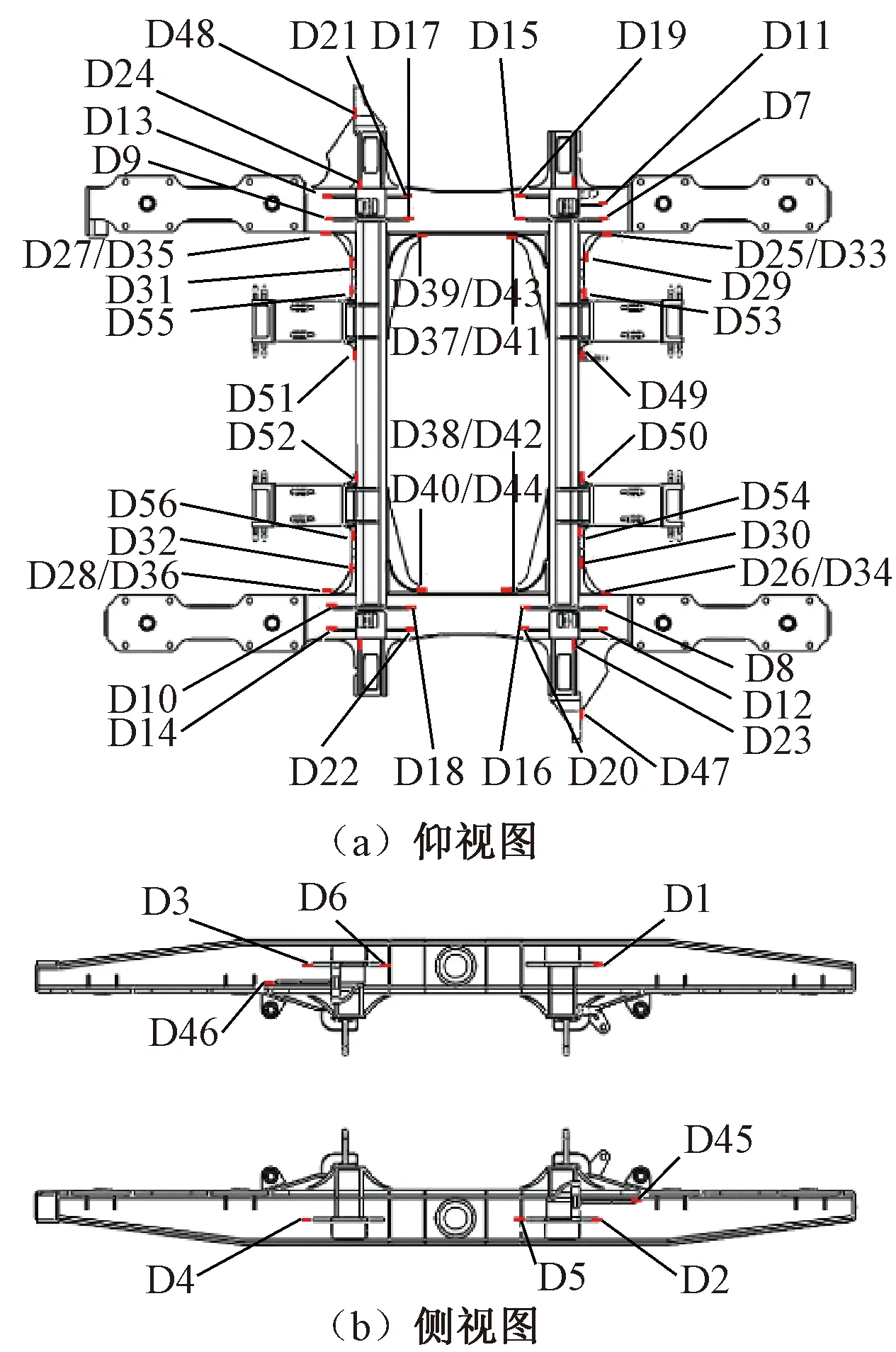
图2 构架典型应力测点示意图
图3为典型工况下构架浮沉载荷系和扭转载荷系的实测时域历程。
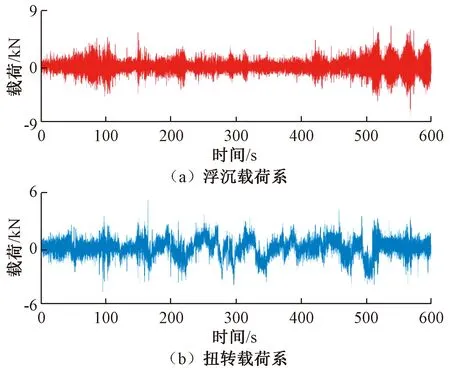
图3 构架浮沉载荷系和扭转载荷系实测时域历程
在文献[12]对构架载荷系进行解耦识别的基础上,对实测获取的构架各载荷系的时间历程分别进行雨流计数处理,并扩展至构架全寿命运用里程(1 200万km),可以获得与各载荷系对应的载荷谱(本文称之为分立载荷谱)。与浮沉载荷系和扭转载荷系对应的八级分立载荷谱见表1。

表1 浮沉载荷系和扭转载荷系分立载荷谱
2 构架试验载荷谱的编制
编制适用于构架可靠性定量考核的试验载荷谱需要满足两个基本条件:一是能够正确再现构架运用损伤情况;二是便于加载实现。
要正确再现构架运用损伤情况,关键是加载时要使各载荷系之间的相位关系与实际运用情况基本一致,理论上可以通过同步施加实测获得的各载荷系时域历程来实现,但是对加载设备和工装要求比较高,不便于加载实现。
对于一般的加载设备,施加分段恒幅的同频正弦波载荷是最方便的。在这样简便的加载方式下,如何使各载荷系之间的相位关系能够与实际运用中构架各载荷系之间复杂的相位关系总体一致,是需要解决的核心问题。
下面依次讨论各载荷系恒幅载荷谱的编制和各载荷系分立载荷谱之间相位的匹配问题。
2.1 载荷系恒幅载荷谱
在获得表1形式的载荷系分立载荷谱后,可进一步依据损伤等效原则建立载荷系恒幅分立载荷谱。由于各级载荷的幅值和频次不同,其产生的损伤也不相同。在建立载荷系恒幅分立载荷谱时,均以该载荷系分立载荷谱中产生损伤最大的载荷级为基准,具体的等效方式为[13]
(1)
式中:neq为等效后的恒幅分立载荷谱循环次数;Aeq为分立载荷谱中产生损伤最大的载荷级的载荷幅值,是等效后恒幅分立载荷谱的载荷幅值;i为分立载荷谱中的第i级载荷;k为分立载荷谱总级数,取8;ni为分立载荷谱第i级载荷的循环次数;Ai为分立载荷谱第i级载荷幅值;m为S-N曲线的斜率,对于焊接构架,m取3.5。
相对于构架全寿命运用里程(209P转向架构架为1 200万km),经过上述等效后获得的恒幅分立载荷谱的循环次数有可能远超出正常试验时的加载次数,此时需要对恒幅分立载荷谱的循环次数进行必要的压缩。由于各分立载荷谱的循环次数不同,为方便加载实现和载荷谱编制,还需考虑各分立载荷谱循环次数之间的相对关系,对循环次数进行适当的圆整。上述压缩和圆整均须按照损伤等效原则进行[13]。
下面以浮沉载荷系作为基准载荷系来确定各载荷系的恒幅载荷谱。依据表1对各级载荷产生的损伤进行比较[11],可以确定最大损伤等级为第3级,将各级载荷根据式(1)向第3级等效。等效后浮沉载荷系恒幅分立载荷谱载荷幅值Ave=2.94 kN,循环次数nve=8.22×108次。
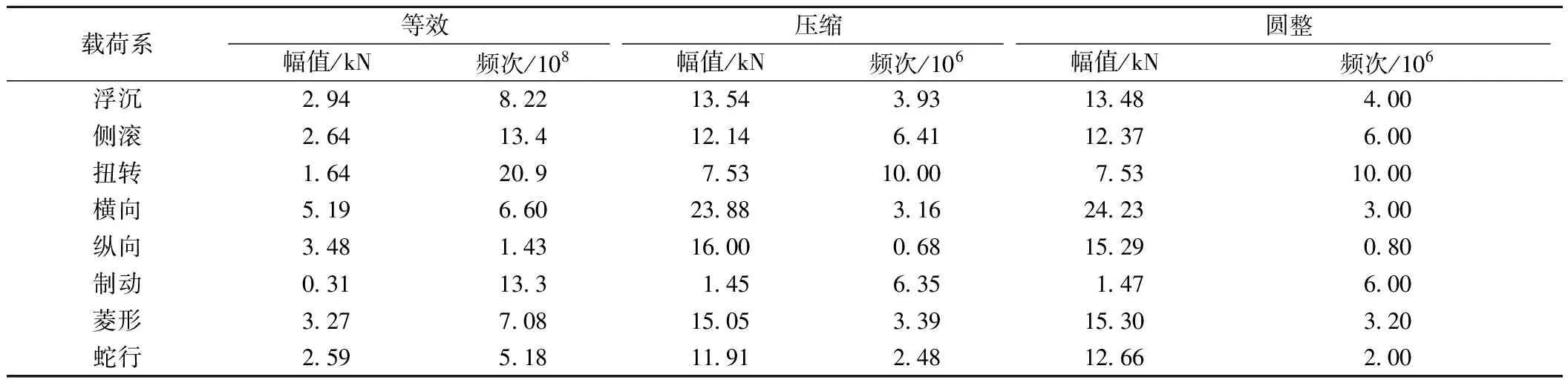
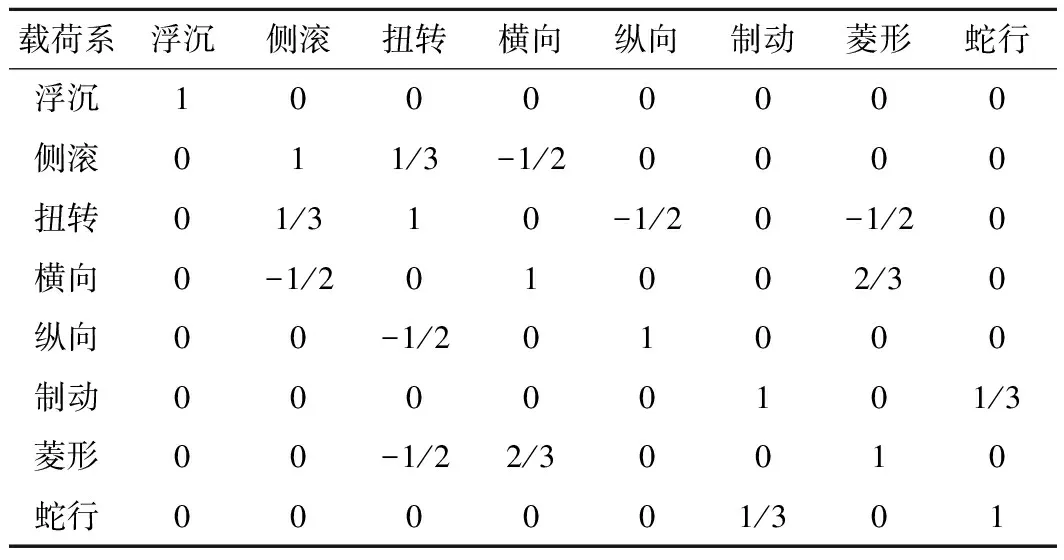
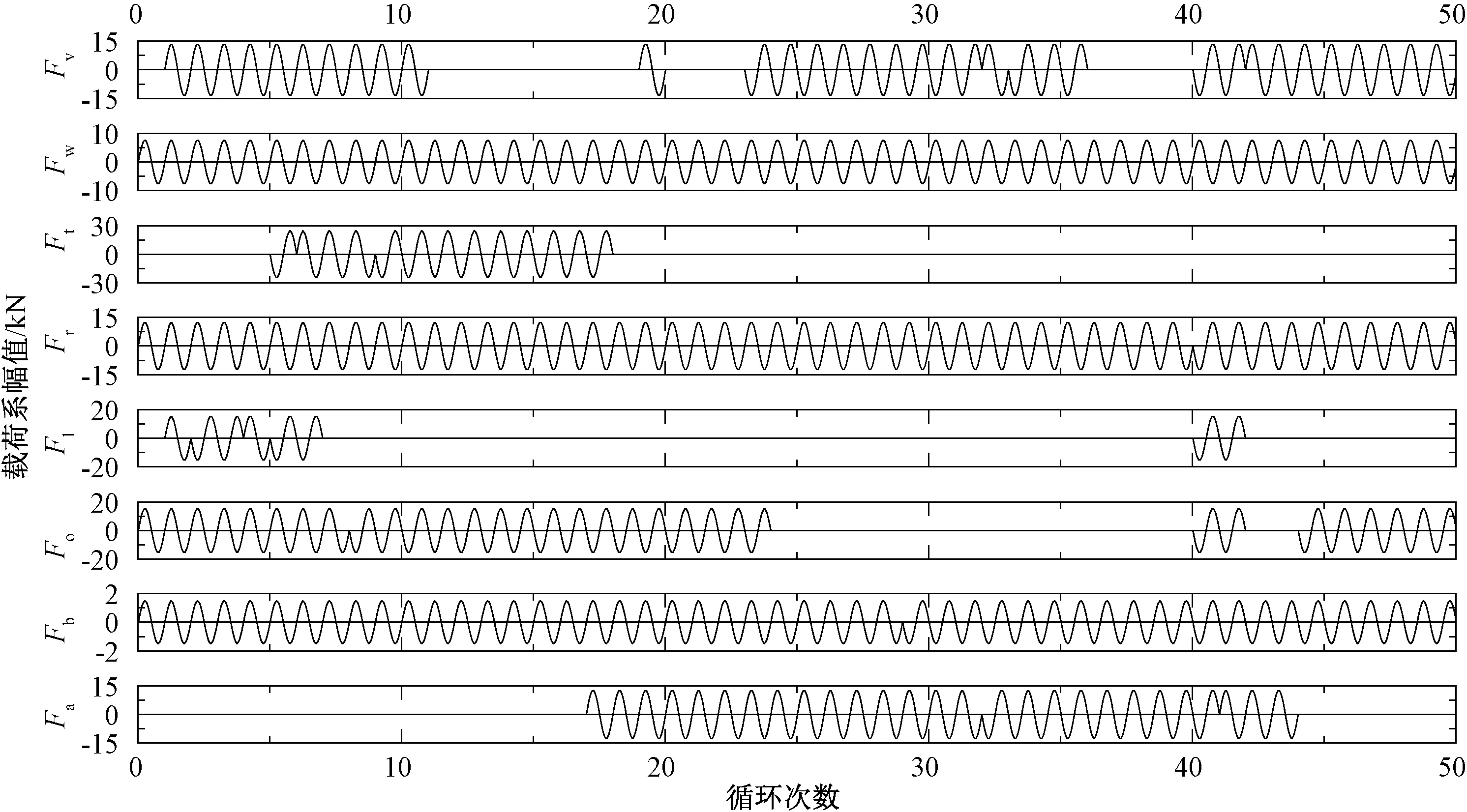
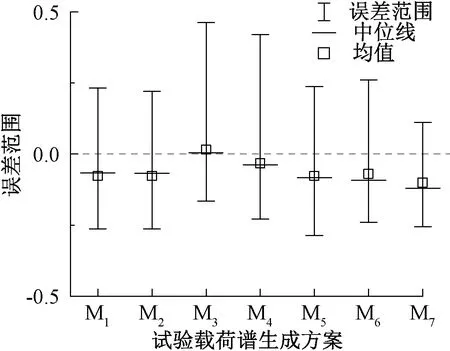
构架可靠性试验加载次数通常为1 000万次[14-15]。作为构架可靠性试验基准载荷系的浮沉载荷系,试验次数取为1 000万次;按照损伤等效原则,对应的载荷幅值Avy=10.37 kN。当其他载荷系等效后的循环次数大于基准载荷系循环次数nve时,依然将其压缩至1 000万次,同时得到损伤等效载荷幅值。例如,扭转载荷系损伤等效后恒幅分立载荷谱的载荷幅值Awe=1.64 kN,循环次数nwe=2.09×109次。nwe大于nve,则需压缩至1 000万次,对应的损伤等效扭转载荷系载荷幅值Awy=7.53 kN。当其他载荷系等效后的循环次数小于基准载荷系循环次数nve时,则选择与基准载荷系相同的压缩系数k(k=nwe/107)进行压缩并确定对应的损伤等效载荷幅值。例如,菱形载荷系损伤等效后恒幅分立载荷谱的载荷幅值Aoe=3.27 kN,循环次数noe=7.08×108次。noe 为方便载荷谱编制,通常还需要对某些载荷系的循环次数做进一步的圆整,并依据损伤等效原则对载荷幅值进行相应的调整。例如,表2中对纵向载荷系压缩后循环次数1.73×106次进一步圆整,圆整后循环次数为2.00×106次,对应的等效载荷幅值为11.76 kN。应当说明的是:各载荷系在频次圆整时,应参考该载荷系与基准载荷系之间的简化相关系数。例如,表3中菱形载荷系压缩后循环次数为3.39×106次,与扭转载荷系的简化相关系数为-1/2,圆整为3.20×106次时,反向同步加载按3/4配置,同向同步加载按1/4配置,此时编制试验载荷谱比较方便。 以浮沉载荷系为基准载荷系时,各载荷系等效、压缩和圆整后得到的恒幅载荷谱见表2。 以各载荷系恒幅分立载荷谱(见表2前两列数值)中循环次数最多的扭转载荷系为基准载荷系,则各载荷系在等效、压缩和圆整后得到的恒幅载荷谱见表3。 表2 各载荷系等效、压缩和圆整后的载荷幅值和循环次数 表3 各载荷系等效、压缩和圆整后的载荷幅值和循环次数 作者所在团队的初步研究表明:载荷系之间的相位关系可以借助载荷系时域历程之间的相关系数表征[10-11]。选用Pearson相关系数来描述载荷系之间的相关性,具体[16]为 (2) 由式(2)可知,Sx和Sy不能为零;x和y在计算相关性时具有互换性,也就是x对y的相关系数与y对x的相关系数相同;相关系数r是无量纲量,r∈[-1,1],|r|越大,表明两者之间相关性越强[16]。 采用209P转向架构架在赤峰至大连区段运营线路上实测的载荷-时间历程为数据样本,各载荷系样本标准差分布在0.35~2.8,均不为零。由式(2)计算的各载荷系之间的相关系数,见表4。 表4 各载荷系之间的相关系数 一般说来,当相关系数为0.8≤|r|≤1时,两者视为强相关;当相关系数为0≤|r|<0.3时,两者视为弱相关;当相关系数为0.3≤|r|<0.8时,两者视为相关。 为方便后续试验载荷谱编制,若载荷系之间为强相关,则近似处理为完全相关,相关系数取为1;若载荷系之间为弱相关,则近似处理为不相关,相关系数取为0;当0.3≤|r|<0.8时,简化处理方式在第2.3节详细讨论。 将各载荷系之间的相位关系用载荷谱相位矩阵表征。因此,编制载荷谱相位矩阵就成为编制试验载荷谱的关键。为便于编制载荷谱相位矩阵,需要对表4中给出的相关系数进行简化。下面介绍一种实践证明切实可行的简化方案。 当两个载荷系之间强相关(0.8≤|r|≤1)时,|r|=1;相关系数为正时,两载荷系同向同步加载;相关系数为负时,两载荷系反向同步加载。 当两个载荷系之间弱相关(0≤|r|<0.3)时,r取0;两载荷系之间可同向同步加载,也可反向同步加载,且两者出现的概率相同。例如浮沉载荷系和侧滚载荷系之间相关系数为r=0.023,取r=0;以浮沉载荷系正向加载为例,浮沉载荷系与侧滚载荷系加载时的相位关系见表5,“+”表示正向,“-”表示负向。 表5 浮沉和侧滚载荷系相位关系 当两个载荷系之间相关(0.3≤|r|<0.8)时,两载荷系之间加载的相位关系既与相关系数的符号有关,也与相关系数的大小有关。 下面考虑简化为三种情况:当0.3≤|r|<0.5时,r取1/3;当0.5≤|r|<0.67时,r取1/2;当0.67≤|r|<0.8时,r取2/3。例如扭转载荷系与纵向载荷系相关系数为r=-0.612,简化相关系数取-1/2;即反向同步加载的概率比同向同步加载的概率多出1/2,以扭转载荷系正向加载为例,扭转载荷系与纵向载荷系加载时的相位关系,见表6。 表6 扭转和纵向载荷系相位关系 以上有关载荷系相关系数以及载荷相位关系的简化处理方式,是在充分考虑实际加载便利性的基础上,经过对比筛选后确定的可行方式,具体见第3节。 各载荷系之间的简化相关系数见表7。 综合考虑表3中各载荷系恒幅载荷谱循环次数比值和表7中各载荷系之间的简化相关系数,并按照前述载荷相位简化处理方式,以扭转载荷系为基准载荷系,可以编制出周期为200个加载循环的载荷谱相位矩阵,见图4。图中正向加载用1表示,反向加载用-1表示,空载用0表示。 图4 载荷谱相位矩阵 表7 各载荷系之间的简化相关系数 为便于构架可靠性试验加载,采用同频正弦加载方式编制构架试验载荷谱。以表3所示的各载荷系恒幅载荷谱载荷幅值作为同频正弦波幅值,结合图4所示的载荷谱相位矩阵,可以生成试验载荷谱载荷时域信号。由于篇幅所限,图5仅表示与基准载荷系前50个加载循环对应的试验载荷谱的载荷时域信号。实际加载时,图5中的每个循环可以重复若干次;如重复1 000次时,全部1 000万次加载可以划分为50个加载模块,每个模块加载20万次。 图5 试验载荷谱载荷时域信号 试验载荷谱对应的构架损伤(本研究以等效应力度量损伤)与构架实测载荷系时域历程对应的构架损伤是否一致,是检验构架试验载荷谱编制成功与否的根本标准。 如果同步施加构架各载荷系实测时域历程,可以完全保证各载荷系之间的相位关系与实际运用情况一致。尽管在实际加载时这种情况难以实现,但对于仿真计算而言并无困难。由载荷谱计算等效应力时,需要用到载荷系与应力之间的传递系数,详见文献[12];等效应力的计算方法见文献[5]。图6(a)为以扭转载荷系为基准载荷系建立的构架试验载荷谱预测的构架各关键部位的等效应力,与构架各载荷系实测时域历程预测的等效应力的对比情况。由图6(b)可知,试验载荷谱预测的等效应力与实测载荷系时域历程预测的等效应力两者的比值,多数均在0.8~1.1;最小0.74,最大1.23。 总体来看,本文编制的构架试验载荷谱既方便于构架可靠性试验加载实现,又能够良好再现构架实测载荷系时域历程对应的损伤情况,适合于构架运用可靠性定量考核;构架试验载荷谱编制方法思路清晰、过程简洁,便于应用。 为研究基准载荷系对试验载荷谱编制效果的影响,分别以浮沉载荷系和侧滚载荷系作为基准载荷系编制了构架试验载荷谱,所预测的等效应力与实测载荷系时域历程预测的等效应力的比值分别见图6(b)和图6(c)。 由图6(b)和图6(c)可知,选择浮沉载荷系或侧滚载荷系作为基准载荷系时,构架试验载荷谱总体上均能够良好再现实测载荷系时域历程预测的构架损伤。个别测点(D45)误差较大,且在图6所示的3种情况下具有一致性,有可能是该测点的载荷系与应力传递系数标定误差过大所致[13]。从载荷系恒幅分立载荷谱的频次来看(见表2第二列),以上3种情况中,扭转载荷系最多、侧滚载荷系次之,浮沉载荷系最少。对应地,编制出的载荷谱相位矩阵,扭转载荷系最短,200个循环;侧滚载荷系次之,240个循环;浮沉载荷系最长,480个循环,见表8。 此外,还对载荷系相关系数简化方式和载荷谱相位矩阵排列次序的影响情况进行了分析比较。试验载荷谱与实测载荷系时域历程预测的等效应力之间的相对误差可以表示为 ηi=(σmi-σti)/σti (3) 式中:σmi为第i个测点试验载荷谱预测等效应力;σti为第i个测点实测载荷系时域历程预测的等效应力。 表8中,M1和M2方案的载荷谱相位矩阵排列次序不同;M1、M2、M3、和M4方案的载荷系相关系数简化方式相同;M1、M3和M4方案分别对应图6(a)、图6(b)和图6(c);M5、M6和M7三种方案对于载荷系相关系数的简化方式更为简单。 表8中所列各方案编制的试验载荷谱预测的等效应力与实测载荷系时域历程预测的等效应力之间的相对误差见图7。由图7可知,M1和M2方案的误差范围较小且两者相差不大,预示载荷谱相位矩阵排列次序对等效应力预测效果影响不大。将M5至M7方案与M1至M4方案比较可知,载荷系相关系数的简化方式对等效应力预测效果的影响也比较小。 表8 试验载荷谱编制方案 图7 各方案试验载荷谱预测等效应力与实测载荷系时域历程预测等效应力的相对误差 总体来看,M1~M7各方案对于等效应力的预测效果都比较好,意味着采用本文方法编制构架试验载荷谱时,对于基准载荷系、载荷谱相位矩阵排列顺序,特别是载荷系相关系数简化方式选择比较灵活,便于推广应用。 对构架实测载荷时间历程进行雨流计数,获得了构架各载荷系分立载荷谱;在此基础上,依据损伤等效原则,选取基准载荷系,通过向分立载荷谱损伤最大载荷级等效、载荷频次压缩和圆整,给出了适合构架试验载荷谱编制的载荷系恒幅载荷谱。采用构架各载荷系实测时域历程,计算各载荷系之间的相关系数并适当简化,可以获得适合构架试验载荷谱编制的载荷系简化相关系数。结合各载荷系恒幅载荷谱和简化相关系数,可以构造出载荷谱相位矩阵,并进而建立构架试验载荷谱。 构架试验载荷谱预测的构架损伤结果,与构架载荷系实测时域历程预测结果吻合良好,适合于构架运用可靠性定量考核;试验载荷谱编制方法思路清晰、过程简洁、易于加载实现;该方法对于基准载荷系、相关系数简化方式以及载荷谱相位矩阵排列次序在选择上均允许有较大的灵活性,方便载荷谱编制;表明本研究建立的构架试验载荷谱编制方法不仅成功,也便于应用。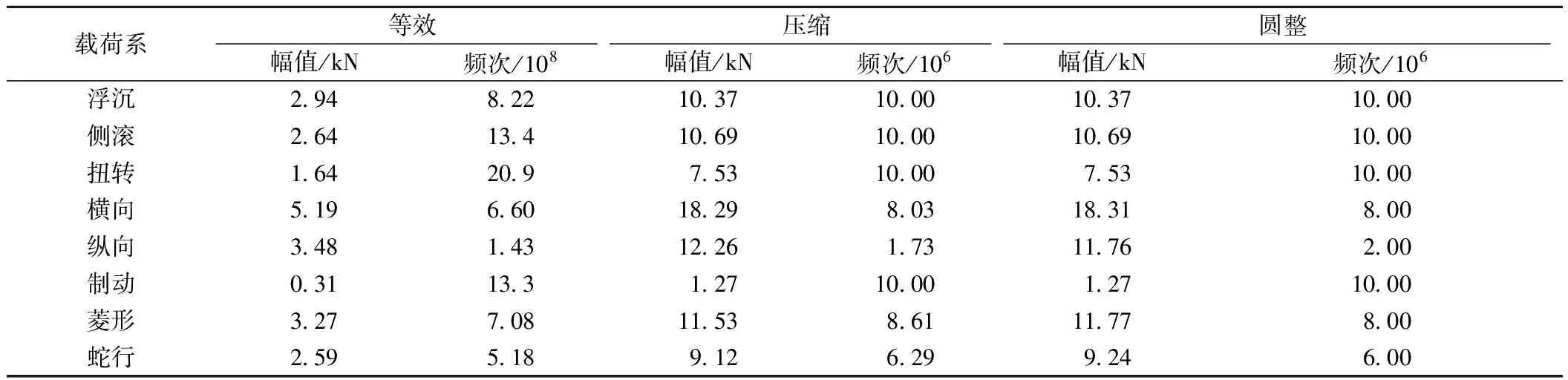
2.2 载荷系相关性分析
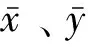

2.3 载荷谱相位矩阵的编制



2.4 试验载荷谱的编制
3 构架试验载荷谱可行性验证
4 讨论

5 结论

