一种分段分块式压缩采样模型的设计
方 标, 黄高明, 高 俊, 左 炜
(1. 海军工程大学 电子工程学院,湖北 武汉 430033;2. 中国人民解放军92723部队,北京 100841)
香农/奈奎斯特采样定理指出:为避免信息丢失,实现无失真恢复原始信号,采样率至少要两倍于信号带宽.所以,宽带模拟信号的数字化需要很高的采样率.由于器件的物理特性约束,提高采样率的代价是巨大的,如导致量化精度下降等.压缩感知(Comoressive Sensing,CS)[1-2]理论为解决上述问题开启了新的思路,其思想是对稀疏信号以远低于奈奎斯特频率的采样率进行全局观测而非局部采样,然后用适当的重构算法从观测值中还原出原始信号.
CS理论的提出最初是针对离散数字信号的,为了将其应用到模拟域,就出现了基于压缩感知理论的模拟到信息的转换理论,其旨在利用信号的结构特征降低信号采样率,解决海量数据的压缩存储以及传输问题.模拟到信息转换的研究重点在于采用何种有效的转换架构,使得信号采集效率得以提高,采集方式的适用范围得以扩展.在近几年不断发展过程中,涌现了一批各有特色的转换架构.最早的模拟信息转换方式可以追溯到多陪集采样模型(Multi-coset Sampling,MS)[3],它是在周期非均匀采样基础上提出的一种结构简单、易于硬件实现的并行支路模型,已应用于稀疏信号的数据采集,但存在一些固有的缺陷,比如处理信号的最大带宽受限于模数转换器(Analog to Digital Converter,ADC)的固有带宽,两个ADC之间保持精确的时间偏移量在实际环境中存在困难[4].在CS理论提出后,Laska等提出了随机采样模型(Random Sampling,RS)[5],主要用于采集和处理局部傅里叶稀疏信号(Local Fourier Sparse,LFS),即信号的每个时间点能够近似地分解成几个定频的正弦波的宽带信号,比如部分跳频通信信号、雷达信号和大部分的语音信号,文献[5]给出了一个RS在宽带信号中的典型应用.随机解调模型(Random Demodulation,RD)[6-7]是一个由宽带周期伪随机解调器、模拟低通滤波器和低速A/D采样器组成的单支路模拟到信息转换结构,目前应用范围比较广,文献[6]将这一模型推广到频谱稀疏的连续域多频带信号类型中,但此模型对滤波器的设计要求很高,滤波器设计对可重构性的影响非常大.在并行架构方向,Eldar团队提出了调制宽带转换器模型(Modulated Wideband Converter,MWC)[8-9],这一架构克服了多陪集模型的两大缺陷:MWC利用伪随机序列函数通过混频操作实现频谱搬移,摆脱了模拟ADC带宽的限制;同时各支路采用同一个时间触发器保证了采样同步,有效解决了精确的时间延迟难以实现的问题.但其本身存在一个问题:当单位时间内需要很多的压缩采样值时,将导致相当大数量的相关支路,这将大大增加系统硬件实现的复杂度.针对此问题,文献[10]加入分段思想对MWC进行了改进,提出了分段式模拟信息转换器(Segmented Analog-to-Information Conversion,S-AIC),在每个混合积分器支路(Branches of Mixters and Integrators,BMIs)上将每一个积分周期分成M段后,得到分段测量值;再按照一定规则将各个BMIs上的分段测量值置换,得到新测量值,达到在不增加BMIs的基础上扩展测量矩阵行数的目的,有效降低了相关支路数,提升了恢复性能.但是,由于S-AIC所得的等效测量矩阵是密集矩阵,其硬件实现的复杂度高.针对测量值密集性问题,文献[11]从集合论和互相关理论出发,通过去除冗余观测达到降低观测信号数的目的.笔者在积分周期分段的基础上,对BMIs和积分时间进行分块处理,提出了基于分段分块采样的模拟信息转换器(Segmented and Blocked Analog-to-Information Conversion,SB-AIC),将等效测量矩阵转换为稀疏块对角矩阵,缩短了积分时间.该模型不仅能够改善传统AIC的恢复性能,而且相比S-AIC降低了硬件实现的难度.
1 S-AIC模型描述
针对如何降低普通并行AIC,如MWC结构中BMIs的数量,节约硬件成本的问题,文献[10]提出了一种分段型AIC(S-AIC),其基本思想是重复利用压缩采样值构建新采样值.从矩阵形式上看,这等价于对观测矩阵进行扩展,增加观测矩阵的行数,然后利用该观测矩阵获取新的压缩采样值,来提高系统的恢复性能,降低系统的相关采样支路,从而达到降低系统硬件实现成本的目的.S-AIC与AIC的构成部件和工作原理相同,它们之间的不同之处在于:并行压缩采样模型每次重构过程只采用了每个通道的1个采样点,而分段式并行压缩采样模型中每个通道的多个连续采样点参与信号重构.实现分段采样的关键是如何利用不完整的压缩采样值构建新的测量值,其具体的实现结构如图1所示.每一个支路中输入信号x(t)与周期伪随机序列p(t)的相乘结果,再由分段后脉冲响应为h(t)的积分器滤波,后经低速ADC以子奈奎斯特采样率fs采集数据.其中,频率fs的选取与滤波器的截止频率有关,p(t)是一个取值为 ±1 有限持续时间随机方波的周期扩展.这一模型在原来支路数量不变的情况下,采用扩展后的测量矩阵观测信号能够获得更多的信息样点,也就是说,在所需信息样点数目一定的条件下,改进后转换模型的相关支路数量减少了.文献[12]指出,如果原来矩阵满足受限等距性质(Restricted Isometry Property,RIP),那么扩展后的测量矩阵也以一定概率满足RIP条件,可知改进后的测量矩阵能够继承RIP特性.

图1 分段式压缩采样(S-AIC)结构示意图
2 SB-AIC模型的设计与分析
2.1 SB-AIC模型的设计思想
由于结构化的测量矩阵能够节省存储空间、降低计算复杂度,并且满足RIP特性[12].鉴于此,在S-AIC基础上,对积分时间和BMIs进行分块操作,将S-AIC中的子采样K×M矩阵Y进一步分割成若干个对角化块,使得等效测量矩阵Φe为块对角矩阵,除了主对角线外其他元素均为0,在每一个独立的对角块中进行类似于前文中的S-AIC处理,从而降低硬件复杂度.
图2显示了SB-AIC的结构框图,其基本思想是将S-AIC的大测量矩阵分割成若干个相对独立的对角块小测量矩阵,在每一个小块中按照S-AIC的扩展思路产生新测量值,这样除对角块外的测量值就全部置零,复杂度大大降低,存储空间也会大大缩小,进一步提高了模型的适用性.分块思想是SB-AIC的核心,也是其与S-AIC模型的主要区别,下节将就这一主要差别进行分析.
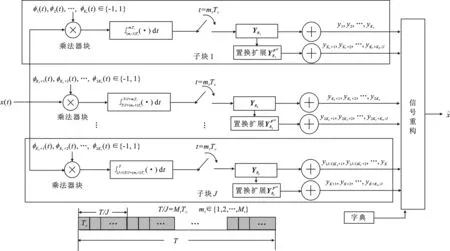
图2 分段分块式压缩采样(SB-AIC)结构示意图
2.2 SB-AIC模型分析
在SB-AIC中,K个BMI被分成J块,假设K和M是J的整数倍,令Mt=M/J,Kt=K/J,Nt=N/J.第j(j=1,2,…,J)块包含从 (j-1)Kt+1 到jKt共Kt个BMI.对于第j块中的每一个BMI,其积分时间是从 (j-1)T/J到jT/J,则SB-AIC中第j块的所有BMI产生的子采样为下面的Kt×Mt矩阵,即
(1)
定义K×M的块对角矩阵为
Y=diag(YB1,YB2,…,YBJ) ,
(2)
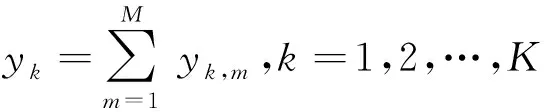
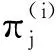
额外的采样值产生:对矩阵Y中的列逐块进行置换,子采样的置换在每个YBj块中独立进行,块内对每一列的置换方式和前述S-AIC中的置换方式相同[13].此时,SB-AIC置换集最多为I=Kt-1 个.将置换集P(i)应用于Y中的每个块中,可得
(3)
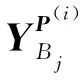
当Ka=KI时,令Ya=[(YP(1))T,…,(YP(I))T]T,则第k个额外的采样值为
(4)
每一个分块都可以看成独立的S-AIC.因此,额外的采样值的产生只与本块内产生的原始采样值有关,而与其他块产生的原始采样值相互独立.
令ΦBj为Kt×Nt的矩阵,其中第k行第n列的元素为
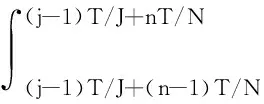
(5)
则SB-AIC的等效测量矩阵为
(6)
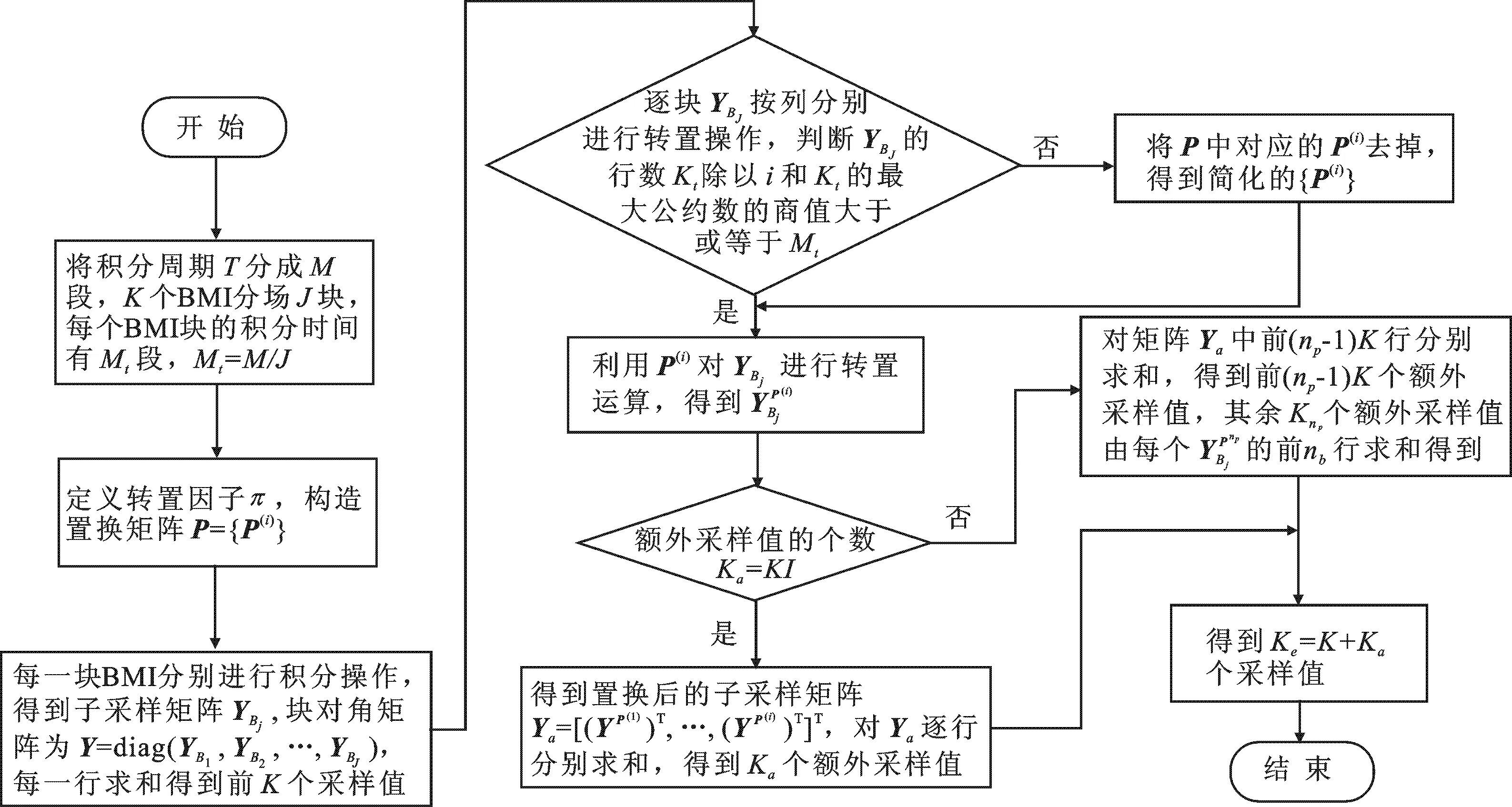
当Ka (7) l∈{1,2, …,nb} . (8) 此时,等效测量矩阵的形式如下: (9) 图3 SB-AIC压缩采样信息处理算法流程图 针对AIC、S-AIC和文中SB-AIC进行仿真测试和分析.仿真设置同参考文献[10],不失一般性和公平性,文中仿真实验中全部采用输入长度N=512,稀疏度S=5 的相同时域稀疏信号,信号中的非零元素为 ±1 等概率分布的时域稀疏信号,即稀疏基Ψ=I.经过AIC后的信息向量y=Φx(t)+e,其中,e是均值为0、方差为σ2的高斯噪声向量.为了保证分段分块后的等效采样值噪声同于原始采样值噪声,按照文献[10],令AIC条件下噪声方差为σ2,S-AIC的子采样噪声方差为σ2/M,SB-AIC中子块采样噪声方差为σ2/Mt. 在无噪背景下,当信号在时域稀疏,选取J=2和J=5两种情况,扩展率(SR)分别取1,2,3,4,5.采用OMP算法重构信号,分别进行100次蒙特卡罗实验.图4给出了该条件下恢复稀疏信号的均方误差(MSE)的性能曲线.由图4可知,当SR大于等于3、J=2 时,SB-AIC与S-AIC的性能基本相同,特别在SR比较高时,J=5 时的性能也明显优于AIC的性能,证明了新方法的可靠性.由于SB-AIC只需要S-AIC的 1/J的运算和存储资源,SB-AIC的复杂度也为S-AIC的 1/J,在针对大容量数据压缩采样时更具有适用性,从实现成本考虑此方案也更可取. 随着J数目的增加,在相同SR下其测量矩阵的稀疏性增强,根据每个BMI子分块占有的Kt=K/J个BMI支路和Mt=M/J个积分段,独立子块矩阵都将变小.需要注意的是,每个独立子块不能过小,过小无法保证扩展后子采样值的相对独立性,从而影响重构性能,如图4所示.因此,在实际应用中,硬件资源的节省有一定的限度,分块数量J不宜过多,在硬件资源满足构建要求时,J尽可能选取得小一些.这需要结合实际硬件资源和重构恢复情况而定. 图4 不同扩展率下4种采样方案的MSE性能曲线(SNR为∞)图5 不同信噪比下4种采样方案的PROB性能曲线(SR为1) 选取扩展率SR为1,在不同的SNR下比较4种方案下的精确重构概率(PROB).由图5可知,当SNR较高时,4种方案的性能接近,这与图4是相吻合的;当SNR较低时,SB-AIC的性能介于AIC和S-AIC之间,这也说明了SB-AIC在S-AIC的基础上为获取结构上的优势牺牲了一定的性能,但是依然可保证其对AIC的优越性.在实际应用中,通过选取合适的分块数J可获得结构和性能上的有效平衡. 图6 不同的扩展率条件下4种采样方案的PROB性能曲线(SNR为10 dB和30 dB) 在不同的扩展率条件下比较各方案的精确重构性能,选取SNR为 10 dB 和 30 dB 为研究对象.由图6可知,在较高信噪比(SNR为 30 dB) 的情况下,4种方案的精确重构概率都能达到90%以上,PROB性能随SR的变化不明显,信号恢复良好,这与图4中描述的MSE性能是相吻合的;在较低信噪比(SNR为 10 dB) 的情况时,随着SR的提升,3种分段方案下的PROB性能都得到了有效改善.由于文中提出的SB-AIC方案构造的测量矩阵是稀疏对角块矩阵,结构上的优势保证了在相同SR条件下,相比S-AIC,只需占用 1/J的存储空间和运算资源.以J=5 为例,在硬件实现时,若使用相同的存储空间,SB-AIC可利用剩余 4/5 的空间继续扩展至SR为5的情形,这时PROB的性能已经达到93%,相比于S-AIC在SR为1情形下的PROB提升了23%,这说明了文中方案在存储空间受限和低信噪比条件下的优越性. SB-AIC相比于S-AIC(可视为J=1时SB-AIC的特例),将测量矩阵从密集矩阵转化为稀疏对角化矩阵,其优越性主要体现在硬件实现时资源节约上,包括前端的高速脉冲发生器、乘法器和积分器资源以及后端的存储器资源,都将降低为原先的 1/J.由仿真实验可以看出,在同样的SR时,由于测量矩阵数据量的减少,使得SB-AIC的性能略有降低,但与S-AIC仍处于同一数量级.换言之,SB-AIC在牺牲一定可容许性能的基础上,提升硬件的利用率是其主要优越性所在. 围绕并行架构中如何降低混合积分支路数以适应大规模压缩采样值场合的问题,在现有的模型上进行了改进.在BMIs数目相同的条件下,S-AIC获得采样值个数要多于传统AIC的,改善了恢复效果,而文中提出的SB-AIC又在S-AIC的基础上,利用分块思想得到块对角化的等效测量矩阵,不仅能够获得比传统AIC多的采样值,而且减少了积分时间,大幅度节省了硬件资源,降低了硬件复杂度.由于每个分块相对独立,在硬件设计中各分块子采样的存储空间可以实现复用,其实时性也要优于S-AIC的,具有很好的实用性和可操作性. [1] Donoho D L. Compressed Sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. [2] Candes E, Romberg J, Tao T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. [3] Herley C, Wong P W. Minimum Rate Sampling and Reconstruction of Signals with Arbitrary Frequency Support [J]. IEEE Transactions on Information Theory, 1999, 45(5): 1555-1564. [4] Eldar Y C, Oppenheim A V. Filter- bank Reconstruction of Bandlimited Signals from Nonuniform and Generalized Samples [J]. IEEE Transactions on Signal Processing, 2000, 48(10): 2864-2875. [5] Laska J, Kirolos S, Massoud Y. Random Sampling for Analog-to-Information Conversion of Wideband Signals [C]//Proceedings of the IEEE Dallas Circuits and System Workshop. Piscataway: IEEE, 2006: 325-328. [6] Kirolos S, Laska J, Wakin M, et al. Analog-to-Information Conversion via Random Demodulation [C]//Proceedings of the IEEE Dallas Circuits and System Workshop. Piscataway: IEEE, 2006: 1183-1186. [7] Tropp J A, Laska J, Duarte M, et al. Beyong Nyquist:Efficient Sampling of Sparse Bandlimited Signals [J]. IEEE Transactions on Information Theory, 2010, 56(1): 520-544. [8] Mishali M, Eldar Y C. From Theory to Practice: Sub-Nyquist Sampling of Sparse Wideband Analog Signals [J]. IEEE Journal on Selected Topics on Signal Processing, 2010, 4(2): 375-391. [9] Mishali M, Elron A, Eldar Y C. Sub-Nyquist Processing with the Modulated Wideband Converter [C]//International Conference on Acoustics, Speech and Signal Processing. Piscataway: IEEE, 2010: 3626-3629. [10] Taheri O, Vorobyov S A. Segmented Compressed Sampling for Analog-to-Information Conversion: Method and Performance Analysis[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 554-572. [11] 宋晓霞, 石光明. 低冗余的压缩感知观测 [J]. 西安电子科技大学学报, 2012, 39(4): 144-148. Song Xiaoxia, Shi Guangming. Low-redundancy Compressed Sensing Measurements [J]. Journal of Xidian University, 2012, 39(4): 144-148. [12] Badjwa W, Haupt J D, Raz G M, et al. Toeplitz-structured Compressed Sensing Matrices [C]//Proceedings of 14th IEEE/SP Workshop on Statistical Signal Processing. Piscataway: IEEE, 2007: 294-298. [13] Candes E, Tao T. Near-optimal Signal Recovery from Random Projections and Universal Encoding from Random Projection and Universal Encoding Strategies [J]. IEEE Transactions on Information Theory, 2006, 52(12): 5206-5245.
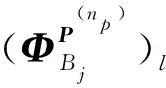
3 仿真实验与分析
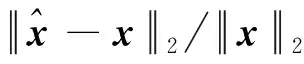
3.1 无噪条件下不同扩展率信号恢复对比实验

3.2 含噪条件下不同信噪比精确重构的对比实验
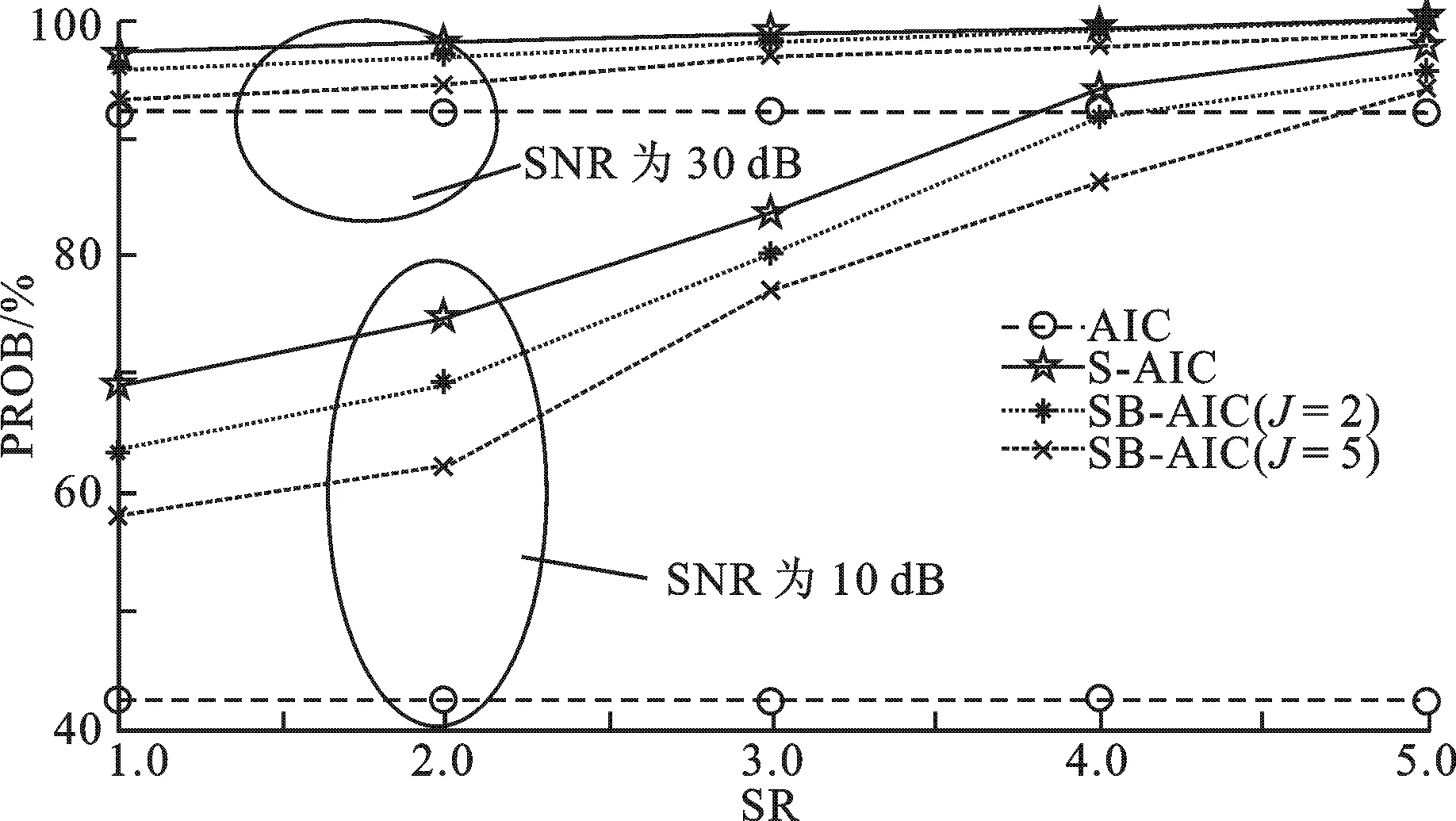
3.3 含噪条件下不同扩展率精确重构对比实验

4 结 束 语

