一种新型分布式互连线功耗优化模型

张 岩， 杨银堂

(西安电子科技大学 宽禁带半导体材料与器件教育部重点实验室，陕西 西安 710071)

近年来，超大规模集成电路集成度的不断提高，互连的功耗、延时和信号完整性已经成为影响集成电路性能和可靠性的决定性因素．2012年，国际半导体技术路线图(ITRS)[1]指出，纳米级工艺的互连线层数已经达到13层，集成电路的互连线长度已经累计达 103m 数量级，虽然单个纳米级集成电路所消耗的功耗不断降低，但是随着互连线层数和长度的持续增加，互连功耗在整个芯片功耗中所占的比重越来越大．因此，如何减小互连线功耗将成为一个研究热点．

传统互连线动态功耗估算中假设互连线等效电容部分消耗能量，因此，功耗模型是针对计算1次激励过程中互连线寄生电容充放电所存储和释放的能量展开研究[2]的，这种方法由于忽略了互连电阻的影响而在计算动态功耗时产生很大的误差．近年互连线功耗估算更多的是计算电流流经互连线时电阻所消耗的热能[3-6]．文献[3]利用Π型电路等效互连树的方法分析互连功耗．文献[4]通过降阶方法估算互连线的等效电流，从而计算互连功耗．文献[5]基于电阻-电容(RC)树形电路模型提出了非理想激励下树形拓扑结构的功耗模型．文献[6]利用互连线频域内传输函数的残数和极点推导出功耗算法．但是以上文献都仅仅建立了功耗模型．实际上，当集成电路工艺技术进入到超深亚微米阶段时，互连线的宽度越来越小，因而不断增加的互连线电阻会产生更大的互连线功耗，甚至占据了整个芯片功耗的30%[4]．随着集成电路工艺技术的进一步提高，互连线功耗所占的比重也越来越大．因此，研究工作将不仅仅停留在如何计算互连线功耗上，更要深一层地研究如何优化互连线的功耗，从而改善互连线性能．

笔者首先基于非理想激励冲激下的集中式互连功耗模型，给出了分布式功耗表达式．考虑到单位电容和单位电阻对互连功耗的影响，提出了一种非均匀互连线的功耗模型，采用数值积分的方法简化了功耗模型的计算过程，并在此功耗模型的基础上，进一步提出了一种基于互连线延时、带宽、面积、最小线宽和最小线间距约束的功耗优化模型；其次，通过对 90 nm 和 65 nm CMOS工艺节点的计算，与未优化模型比较，验证了文中优化模型的有效性；最后，讨论了驱动阻抗和负载电容对互连功耗的影响，以调节驱动电阻和负载电容使所提模型达到最佳效果．

图1 集中式RC互连树结构

1 集总式互连线功耗模型

集总式互连线RC结构可由图1所示的树形模型表示，图中点1，2，…，n表示树节点，两个节点之间部分由1个串联电阻和1个对地电容构成．节点1的一端与输入电压连接，另外一端连接电阻R1和接地电容C1．根据文献[5]，k节点处的Elmore延时可以表示为

(1)

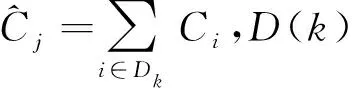
(2)

假设RC互连树的输入电压为指数激励，则其电压可以表示为v(s)=Vdd/(s(1+sτ))，其中，τ为指数电压的上升时间．根据焦耳定律，整个RC互连树功耗模型为

(3)

(4)

图2 分布式互连线模型

2 基于非均匀互连线的功耗优化模型

分布式互连线功耗模型是在集总式RC功耗模型的基础上演变而来的．上一节中基于Elmore延时模型给出了互连树任意一个节点的功耗，并进一步给出了整个互连树的功耗模型．基于这一集总式互连功耗模型，文中提出了一种分布式互连功耗模型．图2为分布式互连线模型，其长度为L，前端驱动电阻为Rd，前端输出电容为Cp，后端负载电容为CL．将互连线等分成n段，每段长 Δx=L/n，每段的电阻和电容分别表示为r(x)Δx和c(x)Δx，其中，r(x)和c(x)分别是互连线在x处的单位电阻和单位电容．一般情况下，前端的输出电容Cp远小于互连线的总电容．因此，在讨论中可以忽略Cp对互连性能的影响．

当n→∞时，根据式(1)～(4)，x点处的延时可以表示为

(5)

整个分布式互连线延时的表达式为

(6)

(7)

其中，α为互连线前级缓冲器的开关因子(一般取0.03)，f为电路工作的频率，

图3 非均匀互连线指数分布线型

为了使互连线达到更好的性能，人们提出了各种各样的技术手段，早在20世纪90年代，非均匀互连线理论就已经建立[7]．非均匀互连线的特点是采用线宽非均匀分布的方法，改变互连线的单位电阻和单位电容，来达到改变互连线性能的目的．非均匀互连线的宽度可看作沿长度方向变化的函数f(x)，互连线的单位电阻和单位电容可分别表示为r(x)=r0/f(x)，c(x)=c0f(x)．直到今天，很多学者仍只是将这一理论应用到减小互连线的延时上[8-12]．从式(7)可以看出，分布式互连的功耗与x点处的单位电阻r(x)和单位电容c(x)有直接的关系．因此，文中采用非均匀互连线的方法来优化功耗．

在前人的研究中，采用最多的非均匀互连线线型分布，包括指数分布和线性分布[8-13]，这里采用指数分布，其结构如图3所示．这种指数分布的线宽函数可以表示为w(x)=w0aexp(-bx)，其中，w0为均匀互连线的线宽，a、b均为正值．

因此，单位电阻的表达式为r(x)=r0exp(bx)/a,

(10)

其中，r0是线宽为w0时，均匀互连线的单位电阻．同理，单位电容可以表示为

c(x)=c0f(x)=ac0exp(-bx) ,

(11)

其中，c0是线宽为w0时，均匀互连线的单位电容．

将式(10)和式(11)代入式(6)～(9)中，得到了非均匀互连线的分布式延时和功耗表达式为

(12)

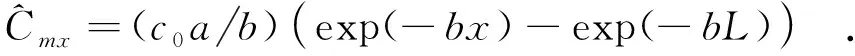
(14)

在具体的应用中，计算Em要经过一个很复杂的积分过程，这会严重影响到模型的计算效率，这里采用了复合Simpson数值积分的方法来简化积分过程．将积分区间[0，L] 5等分,最终式(12)的简化结果为

此处积分区间分成5段，每段积分近似达到4次代数精度，故计算过程是数值稳定的．

如何确定式(16)中的a和b值，以便达到优化功耗的目的是尚待解决的问题．在理论研究中，通常认为功耗越小越好，因而只要求出互连功耗的最小值便可，即对式(15)分别取a和b偏导，求极值．但在实际的设计中，功耗的减小是以牺牲延时为代价的，所以在优化功耗模型时要保证延时与同长度均匀互连线相比不会增大．为了不影响芯片的结构和布局，在采用非均匀互连线时也要确保互连线面积不会大于均匀互连线面积．同时考虑到芯片的数据传输量即芯片的带宽，在建模时非均匀互连线的pitch值不能超过均匀互连线的pitch值．最后，为了满足工艺要求，非均匀互连线的最小线宽和最小线间距同样不能低于工艺所能达到的最小线宽和最小线间距，指数型非均匀互连线在x=L处线宽为其最小线宽，在x=0 处的线间距为整条互连线的最小线间距．

基于上述分析，在确定优化模型的a和b值时，必须满足以下约束条件:

(17)

其中，T0和E0分别是线宽为w0的均匀互连线的延时和功耗，其值可由式(6)和式(7)计算得到；S0=w0L，为均匀互连线的面积；wmin和smin为工艺所能达到的最小线宽和最小线间距．Sm为非均匀互连线的面积，具体表示为

(18)

3 结果和讨论

根据文中所提出的功耗优化模型，在满足约束条件式(17)的情况下，针对 65 nm 和 90 nm CMOS工艺节点做进一步讨论．文中所用到的工艺参数、材料参数以及电参数均来自于模型预测技术[14]，具体的参数值如表1所示．

表1 纳米级CMOS互连线的物理参数和电学参数

利用文中提出的模型和表1所示的参数，计算得到不同长度未优化的均匀互连线和优化后的非均匀互连线的延时和功耗，结果如表2和表3所示，其中，输入电阻Rd=20 Ω，负载电容CL=350 fF．

表2 90 nm 工艺下优化模型和未优化模型的功耗和延时

表3 65 nm 工艺下优化模型和未优化模型的功耗和延时

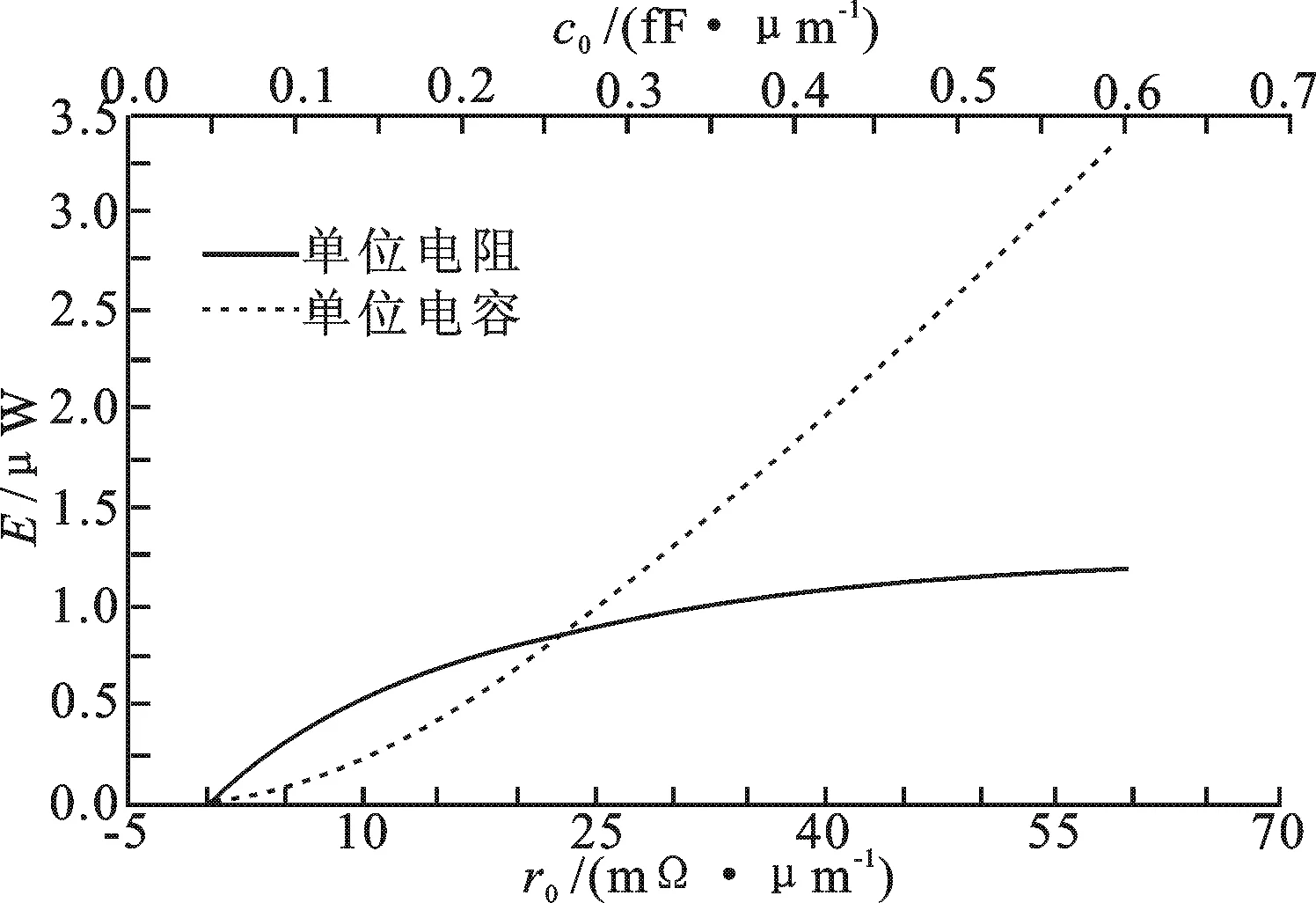
图4 互连线单位长度电阻和单位长度电容与功耗的曲线图

从表2可以看出，相同工艺下文中所提的优化模型可实现降低20%以上的功耗，最高可达30%．表2中数据同样表明，互连线越长，这种优化模型的效果越明显，且长度越长，达到最佳优化效果的a值越大．但是由于带宽和最小线间距的约束，a取值是有上限限制的．当互连线超过一定长度后，a值会停留在其上限而不能满足更长互连线要求的更大a值，导致了模型的优化效果会随着互连线长度的进一步增加而降低．但在长度达到 3 000 μm 时，其优化结果仍然可达30%．表3是 65 nm 工艺下的模型优化结果．虽然与 90 nm 工艺相比，同等长度的互连线功耗优化百分比有所降低，但仍可达18%以上，最大值仍可超过30%．

取得上述优化效果的原因，是非均匀互连线结构对单位长度电阻的改变在功耗方面起到了积极的作用．由图4可以看出，当单位长度电阻和单位长度电容分别增大时，功耗也随之增大．所以，只要减小单位长度电阻值和单位长度电容值就可以降低功耗．

非均匀互连线的平均单位长度电阻可由下式粗略地估算:

(19)

(20)

图5和图6分别表示当负载电容和驱动电阻变化时，优化模型同未优化模型的功耗比较．从图5可以看出，负载电容越小，优化模型效果越好．从图6可以看出，驱动电阻越大，优化模型的功耗减小量所占的比重越大．若将此方法用在互连树的某一段时，Rd可看做是此段互连线的前端总电阻，包括驱动电阻和前端互连树的电阻；CL可看做是后端的总电容，包括负载电容和后端的互连树电容．从而可以通过调节Rd和CL使文中提出的优化模型达到更理想的效果．

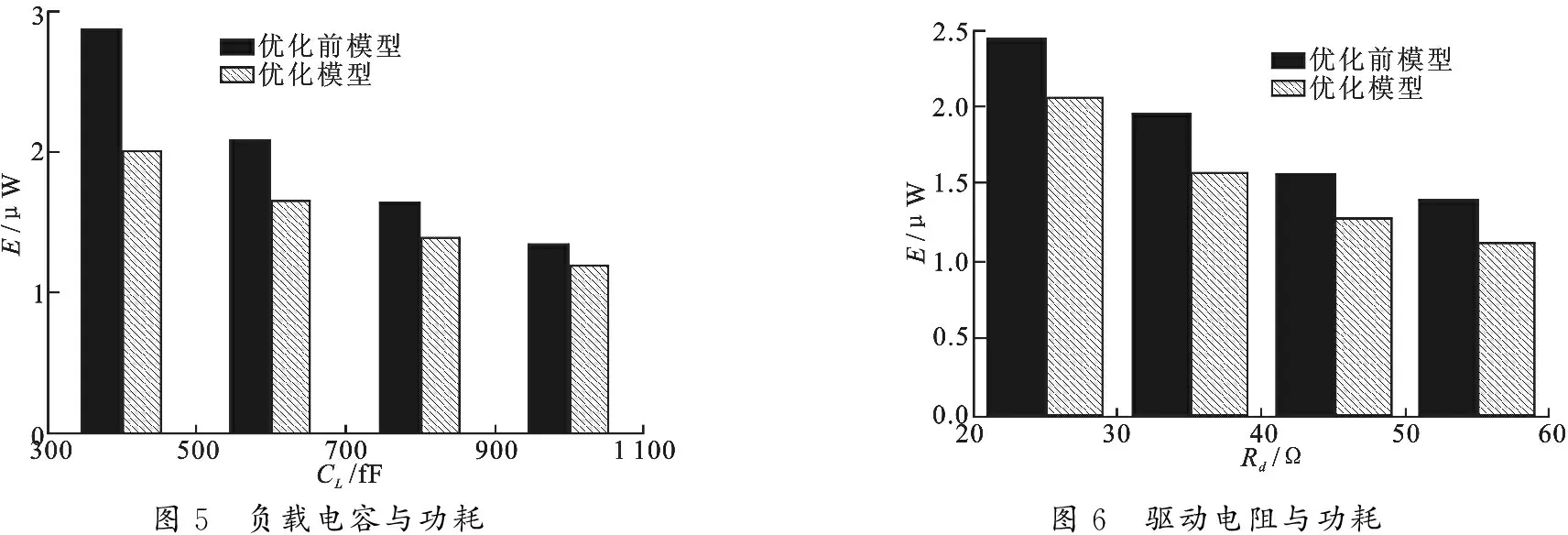
图5 负载电容与功耗图6 驱动电阻与功耗

4 结 束 语

基于互连线的集总式功耗模型，并采用非均匀互连结构推导出非均匀互连的分布式功耗表达式，在此基础上提出了一种基于延时、带宽、面积、最小线宽和最小线间距约束的互连线动态功耗优化模型．文中首先给出了更适合实际研究的分布式互连功耗模型，这一模型能够准确地描绘互连线功耗和延时随着单位长度电阻和电容的变化关系；然后，利用单位长度电阻和电容与互连线宽度的关系，提出了非均匀互连线的分布式功耗模型，并使用数值积分的方法简化了模型的计算过程，在此基础上提出了功耗优化模型；最后，基于 90 nm 和 65 nm CMOS工艺，验证了文中功耗优化模型的有效性，在不牺牲延时、带宽和面积并保证工艺可实现性的前提下，功耗优化的最大比例可达30%以上．该模型对于纳米级CMOS集成电路互连线设计、优化有着重要的指导作用．

[1] Europe, Japan, Korea, Taiwan, USA. Semiconductor Industry Association 2012 International Technology Roadmap for Semiconductors 2012[DB/OL]. [2013-01-02]. http://www.itrs.net.zdz.

[2] Uchino T, Cong J. An Interconnect Energy Model Considering Coupling Effects[J]. IEEE Transactions Computer-Aided Design of Integration Circuits System, 2002, 21(7): 763-776.

[3] 朱樟明, 钟波, 杨银堂. 基于RLC π 型等效模型的互连网络精确焦耳热功耗计算[J]. 物理学报, 2010, 59(7): 4895-4900.

Zhu Zhangming, Zhong Bo, Yang Yintang. An Accurate Joule Heat Model of RLC Interconnect Based on π Equivalent Circuit[J]. Acta Physica Sinica, 2010, 59(7): 4895-4900.

[4] Sahoo S, Datta M, Kar R. An Efficient Dynamic Power Estimation Method for On-Chip VLSI Interconnects[C]//Proceedings of the 2nd International Conference on Emerging Applications of Information Technology. Piscataway: IEEE, 2011: 379-382.

[5] Zhou Q, Mohanram K. Elmore Model for Energy Estimation in RC Trees[C]//43rd ACM/IEEE Design Automation Conference. Piscataway: IEEE, 2006: 965-970.

[6] Kar R, Maheshwari V, Mondal S, et al. A Novel Power Estimation Method for On-Chip VLSI Distributed RLCG Global Interconnects Using Model Order Reduction Technique[C]//International Conference on Advances in Computer Engineering. Piscataway: IEEE, 2010: 105-109.

[7] Chen C P, Chen Y P, Wong D F. Optimal Wire-Sizing Formula Under the Elmare Delay Model[C]//Proceedings of 33rd Design Automation Conference. Piscataway: IEEE, 1996: 487-490.

[8] Lee Y M, Chen C C P, Wong D F. Optimal Wire-Sizing Function Under the Elmore Delay Model with Bounded Wire Sizes[J]. IEEE Transactions Circuits System-Ⅰ: Fundamental Theory and Application, 2002, 49(11): 1671-1677.

[9] EI Moursy M A, Friedman E G. Exponentially Tapered H-Tree Clock Distribution Networks [J]. IEEE Transactions Very Large Scale Integration System, 2005, 13(8): 971-975.

[10] Ni M, Memik S O. Self-Heating Aware Optimal Wire Sizing Under Elmore Delay Model[C]//Proceedings of Design, Automation and Test in Europe Conference and Exhibition. Piscataway: IEEE, 2007: 1373-1378.

[11] Kar R, Maheshwari V, Agarwal V, et al. Modeling of RLC Interconnect Delay for Ramp Input Using Diffusion Model Approach[C]//IEEE Symposium on Industrial Electronics and Applications. Piscataway: IEEE, 2010: 436-440.

[12] Zhang H B, Wong D F, Chao K Y, et al. A Practical Low-Power Nonregular Interconnect Design with Manufacturing for Design Approach [J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2012, 2(2):322-332.

[13] El-Moursy M A, Friedman E G. Wire Shaping of RLC Interconnects [J]. Integration VLSI Journal, 2007, 40(4): 461-472.

[14] University of California Berkeley. Predictive Technology Model[EB/OL]. [2012-12-30]. http://www. eas. asu. edu/～ptm/.